Нестационарные кадры Габора позволяют реализовать временной или частотно-адаптивный анализ сигналов. Функции cqt и icqt использовать нестационарные кадры Габора для получения постоянного Q (частотно-адаптивного) преобразования (CQT) сигнала. Заметной силой нестационарных габорских рам является то, что они позволяют строить стабильные инверсы, давая идеальную реконструкцию.
Теория нестационарных кадров Габора и эффективные алгоритмы их реализации обусловлены [1][2] Дёрфлера, Холигауза, Гриля и Веласко. Алгоритмы в [1] и [2] реализуют блокированную по фазе версию CQT, которая не сохраняет те же фазы, которые были бы получены наивным свертыванием. В [3] Шёркхубер, Клапури, Холигауз и Дёрфлер разрабатывают эффективные алгоритмы для CQT и обратного CQT, которые имитируют коэффициенты, полученные наивным свертыванием. Инструментарий для анализа больших временных частот [4] предоставляет обширный набор алгоритмов для нестационарного анализа и синтеза Габора.
В стандартном анализе Габора окно фиксированного размера перекрывает частотно-временную плоскость. Нестационарный кадр Габора - это совокупность оконных функций различных размеров, которые используются для мозаики частотно-временной плоскости. Вейвлет-анализ выполняет отсечение частотно-временной плоскости аналогичным образом. Вы можете изменять плотность выборки по времени или частоте. Нестационарные кадры Габора полезны в таких областях, как обработка аудиосигнала, где окна с фиксированным размером временных частот не являются оптимальными. В отличие от кратковременного преобразования Фурье, окна, используемые в преобразовании константы-Q, имеют адаптируемую полосу пропускания и плотность дискретизации. В частотном пространстве окна центрированы на логарифмически разнесенных центральных частотах.
Преобразование Фурье f (t) является корреляцией f (t) с ej λ t:
jü tdt.
Поскольку ej λ t не имеет компактной поддержки, преобразование Фурье не является идеальным выбором для изучения нестационарных сигналов. Если частотное содержание сигнала изменяется с течением времени, преобразование Фурье не фиксирует, что это за изменения или когда эти изменения происходят. Показанное здесь разбиение частотно-временной плоскости представляет это поведение преобразования Фурье.
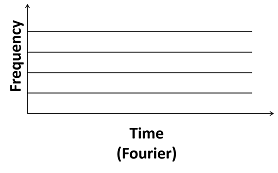
Для выполнения частотно-временного анализа нестационарного сигнала начните с действительной четной оконной функции ), которая фактически ненулевая только на конечном интервале и имеет норму, равную единице. Кроме того, преобразование Фурье t) центрировано в нуле и является низкочастотным. Далее, окно f (t) с трансляциями (t). Тогда возьмите преобразование Фурье результата
− j (t).
Корреляция f (t) с атомами Габора, ej, является стандартным анализом Габора. Изменяя u, вы учитываете только значения f (t) вблизи времени u. g (t) определяет размер окрестности вблизи времени u. Фурье
Концентрация энергии (λ) имеет дисперсию, и она центрирована в λ. Если (t − u) e, смещается на обычной сетке, преобразование Фурье произведения сдвинутого окна и f (t) является кратковременным преобразованием Фурье (STFT). Мозаика STFT частотно-временной плоскости может быть представлена в виде сетки прямоугольников, каждая из которых центрирована в (u, start):
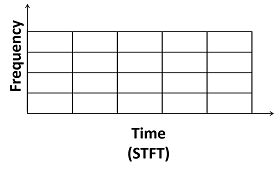
Набор функций } известен как фрейм Габора. Элементы этого множества называются атомами Габора. Кадр - это набор функций, {hk (t)}, удовлетворяющих следующему условию: существуют константы 0 < A ≤ B < ∞ такие, что для любой функции f (t),
Концентрация энергии ), во времени, имеет дисперсию startt. Концентрация энергии (λ), в частотном отношении, имеет дисперсию Концентрация энергии определяет, насколько хорошо окно локализует сигнал по времени и частоте. По принципу временной-частотной неопределенности существует предел того, насколько хорошо вы можете одновременно локализоваться как во временной, так и в частотной областях, как указано
Сужение окна в одном домене приводит к более низкой локализации в другом домене. Габор показал, что площадь окна минимальна, когда ) является гауссовой.
В CQT полоса пропускания и плотность дискретизации по частоте изменяются. Окна создаются и применяются непосредственно в частотной области. Различные окна имеют разные центральные частоты и полосы пропускания, но отношение центральной частоты к полосе пропускания остается постоянным. Поддержание постоянного соотношения подразумевает:
Разрешение во времени улучшается на более высоких частотах.
Разрешение в частоте улучшается на более низких частотах.
Временные сдвиги для каждого окна зависят от полосы пропускания из-за принципа неопределенности.
CQT зависит от:
Оконные функции gk являются действительными, четными функциями. В частотной области преобразование Фурье gk определяется на интервале, [-Fs/2, Fs/2].
Частота взятия проб, λ с.
Количество ячеек на октаву, b.
Минимальную и максимальную частоты, λ min и startmax.
Выберите минимально возможную частоту, а также количество ячеек на октаву b. Затем сформируйте последовательность геометрически разнесенных частот.
λ k = λ min × 2k/b
для k = 0,...,K, где K - целое число, такое, что startK - самая большая частота, строго меньшая, чем частота Найквиста λ s/2. Ширина полосы пропускания на k-ой частоте устанавливается в Λ k = Учитывая эту выборку, отношение k-ой центральной частоты к полосе пропускания окна не зависит от k:
Q = startk/Δk = (21/b-2-1/b) -1.
Для обеспечения совершенной реконструкции компонент постоянного тока и частота Найквиста добавляются к последовательности соответственно.
W (λ) формирует оконные функции gk. W (λ) - действительная, чётная непрерывная функция, центрированная на 0, положительная в интервале [- ½, ½] и 0 в другом месте. W (λ) транслируется на каждую центральную частоту λ k, а затем масштабируется. Оценка масштабированной и преобразованной версии W (λ) дает коэффициенты фильтра gk [m], заданные
gk [m] = W ((m λ s/L - λ k )/Λ k)
для m = 0,..., L-1, где L - длина сигнала. По умолчанию cqt использует 'hann' окно.
По принципу неопределенности размер полосы пропускания ограничивает значение временных сдвигов. Чтобы удовлетворить неравенство кадра, сдвиг akk должен удовлетворять
ak ≤ startk/Startk.
Как упоминалось выше, окно применяется в частотной области. Фильтры, gk, центрированные на, формируются и применяются к преобразованию Фурье сигнала. При обратном преобразовании получают коэффициенты константы-Q.
[1] Холигауз, Н., М. Дёрфлер, Г. А. Веласко и Т. Гриль. «Структура для обратимых преобразований константы-Q в реальном времени». Транзакции IEEE при обработке звука, речи и языка. Том 21, № 4, 2013, стр. 775-785.
[2] Веласко, Г. А., Н. Холигаус, М. Дёрфлер и Т. Гриль. «Построение обратимого преобразования константы-Q с нестационарными кадрами Габора». В материалах 14-й Международной конференции по цифровым аудиоэффектам (DAFx-11). Париж, Франция: 2011.
[3] Шёркхубер, К., А. Клапури, Н. Холигауз и М. Дёрфлер. «Набор инструментов Matlab для эффективного и совершенного преобразования частоты времени реконструкции с логарифмическим разрешением». Представлен 53-й Международной конференции AES по семантическому аудио. Лондон, Великобритания: 2014.
[4] Пруша, З., П. Л. Сёндергаард, Н. Холигауз, К. Висмейр и П. Балаз. Панель инструментов анализа больших временных частот 2.0. Звук, музыка и движение, лекционные заметки по информатике 2014, стр. 419-442. https://github.com/ltfat