Вычисление вейвлет-фильтра Daubechies
dbaux функция генерирует коэффициенты фильтра масштабирования для вейвлетов Daubechies «экстремальной фазы».
W = dbaux(N)N Масштабирующий фильтр Daubechies, который sum(W) = 1.
Примечание
Нестабильность может возникнуть, когда N слишком большой. Начиная со значений N в диапазоне 30, выходной сигнал функции больше не будет точно представлять коэффициенты масштабного фильтра.
Для N = 1, 2 и 3, порядок N Фильтры Symlet и порядок N Фильтры Daubechies идентичны. См. Экстремальная фаза.
Расчет dbN Фильтр масштабирования Daubechies требует извлечения корней многочлена порядка 4N. Нестабильность может возникнуть, начиная со значений N в 30-е годы.
Используемый алгоритм основан на результате, полученном Шенсой [3], показывающем соответствие между фильтрами «Lagrange à trous» и сверточными квадратами вейвлет-фильтров Daubechies.
Вычисление масштабного фильтра w порядка N Daubechies выполняется в два этапа: вычислить фильтр P «Lagrange à troys» и извлечь квадратный корень. Точнее:
P связанный фильтр «Lagrange à trous» является симметричным фильтром длины 4N-1. P определяется
P = [a (N) 0 a (N-1) 0... 0 а (1) 1 а (1) 0 а (2) 0... 0 a (N)]
где
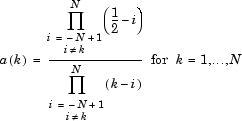
Тогда, если w обозначает dbN Daubechies масштабный фильтр суммы, ![]() w является квадратным корнем из P:
w является квадратным корнем из P:
P = conv(wrev(w), w) где w - фильтр длины 2N .
Соответствующий многочлен имеет N нулей, расположенных в − 1, и N − 1 нулей, меньших 1 в модуле.
Следует отметить, что могут использоваться и другие методы; см. различные решения задачи спектральной факторизации в Strang-Nguyen [4] (стр. 157).
[1] Daubechies, I. Десять лекций по вейвлетам, серия региональных конференций CBMS-NSF по прикладной математике. Филадельфия, Пенсильвания: SIAM Ed, 1992.
[2] Оппенгейм, Алан В. и Рональд В. Шефер. Дискретно-временная обработка сигналов. Энглвуд Клиффс, Нью-Джерси: Прентис Холл, 1989.
[3] Шенса, М.Дж. (1992), «Дискретное вейвлет-преобразование: свадьба a trops и Mallat Algoriths», IEEE Trans. on Signal Processing, vol. 40, 10, pp. 2464-2482.
[4] Стрэнг, Г. и Т. Нгуен. Вейвлетс и банки фильтров. Уэлсли, Массачусетс: Уэлсли-Кембридж Пресс, 1996.