Exponenta Banner
exponenta event banner

idwt

Одноуровневое обратное дискретное 1-D вейвлет-преобразование

свернуть все на странице

    Синтаксис

    x = idwt (cA, cD, wname)
    x = idwt (cA, cD, LoR, HIR)
    x = idwt (___, l)
    x = idwt (___, 'режим', режим)
    x = idwt (cA, [], ___)
    x = idwt ([], cD, ___)

    Описание

    пример

    x = idwt(cA,cD,wname) возвращает одноуровневую одномерную вейвлет-реконструкцию x на основе коэффициентов приближения и детализации cA и cD, соответственно, используя вейвлет, заданный wname. Дополнительные сведения см. в разделе dwt.

    Давайте la быть длиной cA (которая также равна длине cD), и lf длина фильтров реконструкции, связанных с wname (см. wfilters). Если режим расширения DWT установлен на периодизацию, то длина x равно 2la. В противном случае длина x равно 2la- 2lf+2. Дополнительные сведения см. в разделе dwtmode.

    пример

    x = idwt(cA,cD,LoR,HiR) использует указанные фильтры низкочастотного и высокочастотного вейвлет-восстановления LoR и HiRсоответственно.

    x = idwt(___,l) возвращает длину -l центральная часть реконструкции. Этот аргумент можно добавить к любому из предыдущих входных синтаксисов

    x = idwt(___,'mode',mode) использует указанный режим расширения DWT mode. Дополнительные сведения см. в разделе dwtmode. Этот аргумент можно добавить к любому из предыдущих синтаксисов.

    x = idwt(cA,[],___) возвращает одноуровневые восстановленные коэффициенты аппроксимации на основе коэффициентов аппроксимации cA.

    x = idwt([],cD,___) возвращает одноуровневые восстановленные коэффициенты детализации на основе коэффициентов детализации cD.

    Примеры

    свернуть все

    Открыть сценарий в реальном времени

    Продемонстрируйте идеальную реконструкцию с помощью dwt и idwt с ортонормированным вейвлетом. 

    load noisdopp;
[A,D] = dwt(noisdopp,'sym4');
x = idwt(A,D,'sym4');
max(abs(noisdopp-x))
    ans = 3.2152e-12
    Открыть сценарий в реальном времени

    Продемонстрируйте идеальную реконструкцию с помощью dwt и idwt с биортогенным вейвлетом. 

    load noisdopp;
[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('bior3.5');
[A,D] = dwt(noisdopp,Lo_D,Hi_D);
x = idwt(A,D,Lo_R,Hi_R);
max(abs(noisdopp-x))
    ans = 2.6645e-15

    Входные аргументы

    свернуть все

    Коэффициенты аппроксимации, заданные как вектор. cA ожидается, что это будет результат dwt.

    Типы данных: single | double
    Поддержка комплексного номера: Да

    Коэффициенты детализации, заданные как вектор. cD ожидается, что это будет результат dwt.

    Типы данных: single | double
    Поддержка комплексного номера: Да

    Вейвлет, используемый для вычисления одноуровневого обратного дискретного вейвлет-преобразования (IDWT), заданного как вектор символов или строковый скаляр. Вейвлет должен быть распознан wavemngr. Вейвлет происходит из одного из следующих семейств вейвлетов: Daubechies, Coiflets, Symlets, Fejér-Korovkin, Discrete Meyer, Biorthogonal и Reverse Biorthogonal. Посмотрите wfilters для вейвлетов, доступных в каждом семействе.

    Указанный вейвлет должен быть тем же вейвлетом, который используется для получения коэффициентов аппроксимации и детализации.

    Пример: 'db4'

    Фильтры вейвлет-реконструкции, заданные как пара действительных векторов четной длины. LoR является фильтром реконструкции нижних частот, и HiR является фильтром реконструкции верхних частот. Длины LoR и HiR должно быть равным. Посмотрите wfilters для получения дополнительной информации.

    Типы данных: single | double

    Длина центральной части реконструкции, определяемая как положительное целое число. Если xrec = idwt(cA,cD,wname), то l не может превышать length(xrec).

    Типы данных: single | double

    Режим расширения DWT, используемый при вейвлет-реконструкции, задается как вектор символа или скаляр строки. Возможные режимы расширения см. в разделе dwtmode.

    Алгоритмы

    Начиная с коэффициентов приближения и детализации на уровне j, cAj и cDj, обратное дискретное вейвлет-преобразование восстанавливает cAj − 1, инвертируя шаг разложения вставкой нулей и свернув результаты с фильтрами реконструкции.

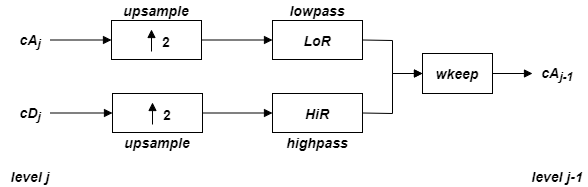
    где

    • - Вставлять нули в четно-индексированные элементы

    • - Свернуть с фильтром X

    • - Возьмите центральную часть U с удобной длиной

    Ссылки

    [1] Daubechies, I. Десять лекций по вейвлетам. Серия региональных конференций CBMS-NSF по прикладной математике. Филадельфия, Пенсильвания: Общество промышленной и прикладной математики, 1992.

    [2] Маллат, С. Г. «Теория разложения сигнала с множественным разрешением: вейвлет-представление». Транзакции IEEE по анализу шаблонов и машинному интеллекту. Том 11, выпуск 7, июль 1989 года, стр. 674-693.

    [3] Мейер, Я. Вейвлетс и Операторы. Перевёл Д. Х. Сэлинджер. Кембридж, Великобритания: Cambridge University Press, 1995.

    Расширенные возможности

    ..

    См. также

    | |

    Представлен до R2006a

    Документация инструментария вейвлет

    Поддержка