Одноуровневое 1-D дискретное вейвлет-преобразование
[ возвращает одноуровневое дискретное вейвлет-преобразование (DWT) вектора cA,cD] = dwt(x,wname)x используя вейвлет, заданный wname. Вейвлет должен быть распознан wavemngr. dwt возвращает вектор коэффициентов аппроксимации cA и вектор коэффициентов детализации cD DWT.
Примечание
Если приложение требует многоуровневой вейвлет-декомпозиции, попробуйте использовать wavedec.
[ возвращает одноуровневый DWT с указанным режимом расширения cA,cD] = dwt(___,'mode',extmode)extmode. Дополнительные сведения см. в разделе dwtmode. Этот аргумент можно добавить к любому из предыдущих входных синтаксисов.
Примечание
Для gpuArray входы, поддерживаемые режимы: 'symh' ('sym') и 'per'. Все 'mode' варианты, за исключением 'per' преобразуются в 'symh'. См. пример одноуровневого дискретного вейвлет-преобразования на графическом процессоре.
Начиная с сигнала s длиной N вычисляются два набора коэффициентов: коэффициенты аппроксимации cA1 и коэффициенты детализации cD1. Свертывание s с помощью фильтра масштабирования LoD, с последующим диадическим прореживанием, дает коэффициенты аппроксимации. Аналогично, свертывание s с вейвлет-фильтром HiDс последующим диадическим прореживанием дает коэффициенты детализации.
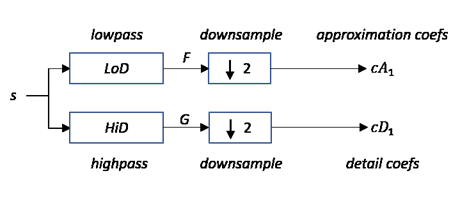
где
![]() - Свернуть с фильтром X
- Свернуть с фильтром X
- Понижение (сохранить четные элементы)
Длина каждого фильтра равна 2n. Если N = длина (длины), сигналы F и G имеют длину N + 2n − 1, а коэффициенты cA1 и cD1 имеют длину 12) + n.
Чтобы справиться с эффектами конца сигнала, вытекающими из алгоритма на основе свертки, глобальная переменная управляется dwtmode определяет тип используемого режима расширения сигнала. Возможные опции включают заполнение нулем и симметричное расширение, которое является режимом по умолчанию.
Примечание
Для того же входа, dwt функция и блок DWT в системной Toolbox™ DSP не дают одинаковых результатов. Блок DWT предназначен для реализации в реальном времени, в то время как программное обеспечение Wavelet Toolbox™ предназначено для анализа, поэтому продукты обрабатывают граничные условия и состояния фильтров по-разному.
Чтобы сделать dwt вывод функции соответствует выходу блока DWT, установить граничное условие функции на нуль-заполнение путем ввода dwtmode('zpd') в командной строке MATLAB ®. Чтобы соответствовать задержке блока DWT, реализуемого с помощью фильтров FIR, добавьте нули на вход dwt функция. Количество добавляемых нулей должно быть равно половине длины фильтра.
[1] Daubechies, I. Десять лекций по вейвлетам. Серия региональных конференций CBMS-NSF по прикладной математике. Филадельфия, Пенсильвания: Общество промышленной и прикладной математики, 1992.
[2] Маллат, С. Г. «Теория разложения сигнала с множественным разрешением: вейвлет-представление». Транзакции IEEE по анализу шаблонов и машинному интеллекту. Том 11, выпуск 7, июль 1989 года, стр. 674-693.
[3] Мейер, Я. Вейвлетс и Операторы. Перевёл Д. Х. Сэлинджер. Кембридж, Великобритания: Cambridge University Press, 1995.
dwtfilterbank | dwtmode | idwt | wavedec | waveinfo