Одноуровневое обратное дискретное 2-D вейвлет-преобразование
x = idwt2(cA,cH,cV,cD,wname)cA и подробные матрицы cH, cV, и cD (горизонтальный, вертикальный и диагональный соответственно) с использованием импульса, заданного wname. Дополнительные сведения см. в разделе dwt2.
Давайте sa = size(, и пусть cA) = size(cH) = size(cV) = size(cD)lf равна длине фильтров реконструкции, связанных с wname. Если режим расширения DWT установлен на периодизацию, размер x, sx равно 2*sa. Для других режимов внутренней линии sx = 2*sa-lf+2. Дополнительные сведения см. в разделе dwtmode.
x = idwt2(___,s)s центральная часть реконструкции с использованием любого из предыдущих синтаксисов.
x = idwt2(cA,[],[],[],___)x на основе матрицы коэффициентов аппроксимации cA.
x = idwt2([],cH,[],[],___)x на основе горизонтальной матрицы коэффициентов детализации cH.
x = idwt2([],[],cV,[],___)x на основе вертикальной матрицы коэффициентов детализации cV.
Загрузите изображение.
load woman whos X
Name Size Bytes Class Attributes X 256x256 524288 double
Переменная рабочей области X содержит изображение. Выполнить одноуровневую вейвлет-декомпозицию X использовать db4 вейвлет.
[cA1,cH1,cV1,cD1] = dwt2(X,'db4');Инвертировать разложение X используя коэффициенты на уровне 1.
A0 = idwt2(cA1,cH1,cV1,cD1,'db4');Проверьте идеальную реконструкцию.
max(abs(X(:)-A0(:)))
ans = 3.4171e-10
Загрузите изображение.
load tartan
imagesc(X)
colormap(gray)
Выполните одноуровневую вейвлет-декомпозицию с помощью db4 вейвлет.
[cA,cH,cV,cD] = dwt2(X,'db4');Получить вейвлет-реконструкцию, используя только диагональные коэффициенты детализации.
xrecD = idwt2([],[],[],cD,'db4');Получить вторую вейвлет-реконструкцию, на этот раз с использованием коэффициентов детализации по горизонтали и диагонали.
xrecHD = idwt2([],cH,[],cD,'db4');Отображение обеих реконструкций.
subplot(1,2,1) imagesc(xrecD) title('Diagonal') subplot(1,2,2) imagesc(xrecHD) title('Horizontal-Diagonal') colormap(gray)
Алгоритм 2-D вейвлет-реконструкции для изображений аналогичен одномерному случаю. Двумерные вейвлет-функции и функции масштабирования получают, принимая тензорные произведения одномерных вейвлет-функций и функций масштабирования. Этот вид двумерного обратного DWT приводит к реконструкции коэффициентов аппроксимации на уровне j из четырёх составляющих: аппроксимации на уровне j + 1, и деталей в трёх ориентациях (горизонтальной, вертикальной и диагональной). На следующей диаграмме описаны основные шаги реконструкции изображений.
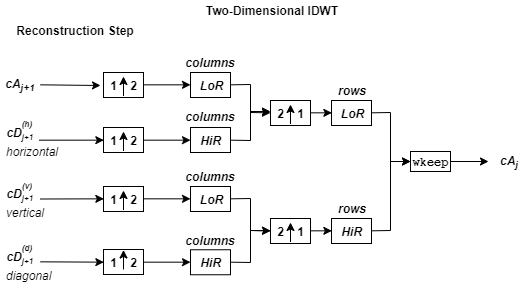
где
- Дополнительные столбцы: вставка нулей в столбцы с нечетным индексом
- Дополнительные строки: вставка нулей в нечетно индексированные строки
- Свернуть с фильтром X строки записи
- Свернуть с фильтром X столбцы записи
[1] Даубехии, Ингрид. Десять лекций по вейвлетам. Серия региональных конференций CBMS-NSF по прикладной математике 61. Филадельфия, Пенсильвания: Общество промышленной и прикладной математики, 1992.
[2] Маллат, С.Г. «Теория разложения сигнала с множественным разрешением: вейвлет-представление». IEEE Transactions on Pattern Analysis and Machine Intelligence 11, No. 7 (июль 1989 года): 674-93. https://doi.org/10.1109/34.192463.
[3] Мейер, Я. Вейвлетс и Операторы. Перевёл Д. Х. Сэлинджер. Кембридж, Великобритания: Cambridge University Press, 1995.