Одноуровневая реконструкция вейвлет-декомпозиции 1-D
[NC,NL,cA] = upwlev(C,L,wname)
[NC,NL,cA] = upwlev(C,L,Lo_R,Hi_R)
upwlev - функция одномерного вейвлет-анализа.
[NC,NL,cA] = upwlev(C,L, выполняет одноуровневую реконструкцию структуры вейвлет-декомпозиции wname)[C,L] предоставление нового [NC,NL]и извлекает последний вектор коэффициентов аппроксимации cA.
[C,L] - декомпозиция на уровне n = length(L)-2, так [NC,NL] является такой же декомпозицией на уровне n-1 и cA - вектор коэффициентов аппроксимации на уровне n.
wname - символьный вектор или строковый скаляр, задающий вейвлет, C - исходный вектор вейвлет-декомпозиции, и L соответствующий вектор учета (подробную информацию о хранении см. в разделе wavedec ).
Вместо указания имени вейвлета можно задать фильтры.
Для [NC,NL,cA] = upwlev(C,L,Lo_R,Hi_R), Lo_R - восстановительный фильтр нижних частот и Hi_R является восстановительным фильтром верхних частот.
% The current extension mode is zero-padding (see dwtmode).
% Load original one-dimensional signal.
load sumsin; s = sumsin;
% Perform decomposition at level 3 of s using db1.
[c,l] = wavedec(s,3,'db1');
subplot(311); plot(s);
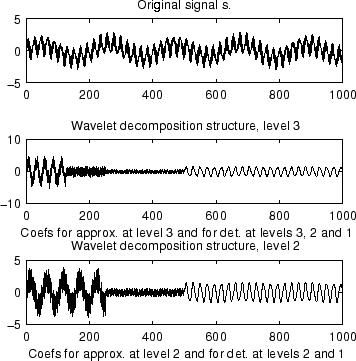
title('Original signal s.');
subplot(312); plot(c);
title('Wavelet decomposition structure, level 3')
xlabel(['Coefs for approx. at level 3 ' ...
'and for det. at levels 3, 2 and 1'])
% One step reconstruction of the wavelet decomposition
% structure at level 3 [c,l], so the new structure [nc,nl]
% is the wavelet decomposition structure at level 2.
[nc,nl] = upwlev(c,l,'db1');
subplot(313); plot(nc);
title('Wavelet decomposition structure, level 2')
xlabel(['Coefs for approx. at level 2 ' ...
'and for det. at levels 2 and 1'])
% Editing some graphical properties,
% the following figure is generated.