Penalized threshold for vullet packet denoising
THR = wpbmpen(T,SIGMA,ALPHA)
wpbmpen(T,SIGMA,ALPHA,ARG)
THR = wpbmpen(T,SIGMA,ALPHA) возвращает глобальное пороговое значение THR для денойзинга. THR получают с помощью правила выбора вейвлет-пакетных коэффициентов с использованием способа пенализации, обеспечиваемого Бирже-Массартом.
T - дерево вейвлет-пакетов, соответствующее декомпозиции вейвлет-пакетов сигнала или изображения, подлежащего деноузированию.
SIGMA - стандартное отклонение нулевого среднего гауссова белого шума в деноизирующей модели (см. wnoisest для получения дополнительной информации.
ALPHA является параметром настройки для штрафного срока. Оно должно быть вещественным числом больше 1. Разреженность вейвлет-пакетного представления деноизированного сигнала или изображения увеличивается с ALPHA. Как правило, ALPHA = 2.
THR минимизирует штрафной критерий, заданный
давайте t* быть минимизатором
crit(t) = -sum(c(k)^2,k≤t) + 2*SIGMA^2*t*(ALPHA + log(n/t))
где c(k) - коэффициенты вейвлет-пакета, отсортированные в порядке убывания их абсолютного значения и n - количество коэффициентов, тогда THR = | c (t *) |.
wpbmpen(T,SIGMA,ALPHA,ARG) вычисляет глобальный порог и, кроме того, строит графики трех кривых:
2*SIGMA^2*t*(ALPHA + log(n/t))
sum(c(k)^2,k£t)
crit(t)
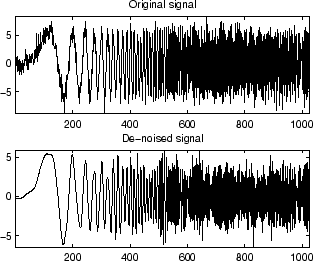
% Example 1: Signal denoising.
% Load noisy chirp signal.
load noischir; x = noischir;
% Perform a wavelet packet decomposition of the signal
% at level 5 using sym6.
wname = 'sym6'; lev = 5;
tree = wpdec(x,lev,wname);
% Estimate the noise standard deviation from the
% detail coefficients at level 1,
% corresponding to the node index 2.
det1 = wpcoef(tree,2);
sigma = median(abs(det1))/0.6745;
% Use wpbmpen for selecting global threshold
% for signal denoising, using the recommended parameter.
alpha = 2;
thr = wpbmpen(tree,sigma,alpha)
thr =
4.5740
% Use wpdencmp for denoising the signal using the above
% threshold with soft thresholding and keeping the
% approximation.
keepapp = 1;
xd = wpdencmp(tree,'s','nobest',thr,keepapp);
% Plot original and denoised signals.
figure(1)
subplot(211), plot(x),
title('Original signal')
subplot(212), plot(xd)
title('De-noised signal')
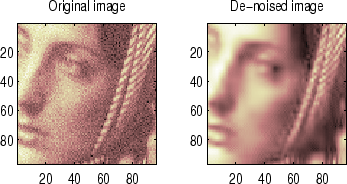
% Example 2: Image denoising.
% Load original image.
load noiswom;
nbc = size(map,1);
% Perform a wavelet packet decomposition of the image
% at level 3 using coif2.
wname = 'coif2'; lev = 3;
tree = wpdec2(X,lev,wname);
% Estimate the noise standard deviation from the
% detail coefficients at level 1.
det1 = [wpcoef(tree,2) wpcoef(tree,3) wpcoef(tree,4)];
sigma = median(abs(det1(:)))/0.6745;
% Use wpbmpen for selecting global threshold
% for image denoising.
alpha = 1.1;
thr = wpbmpen(tree,sigma,alpha)
thr =
38.5125
% Use wpdencmp for denoising the image using the above
% thresholds with soft thresholding and keeping the
% approximation.
keepapp = 1;
xd = wpdencmp(tree,'s','nobest',thr,keepapp);
% Plot original and denoised images.
figure(2)
colormap(pink(nbc));
subplot(221), image(wcodemat(X,nbc))
title('Original image')
subplot(222), image(wcodemat(xd,nbc))
title('De-noised image')