Система sharlet позволяет создавать чувствительные к направлению разреженные представления изображений с анизотропными элементами. Ножницы используются в приложениях для обработки изображений, включая деноизирование, сжатие, восстановление и извлечение признаков. Sharlets также используются в статистическом обучении для решения проблем классификации изображений, проблем обратного рассеяния, таких как томография и разделение данных. Дополнительные приложения можно найти в ShearLab [5].
Сила вейвлет-анализа для 1-D сигналов заключается в его способности эффективно представлять гладкие функции, которые имеют точечные разрывы. Однако вейвлеты не представляют криволинейных сингулярностей, таких как край диска в изображении, так же скудно, как и точечные разрывы. Геометрический многомасштабный анализ - это попытка разработать системы, способные эффективно представлять криволинейные сингулярности в данных более высоких размеров. Помимо шарошек, другие геометрические многомасштабные системы включают криволинейные элементы, контурки и бандлеты.
Го, Кутыниок и Лабате [1] стали пионерами в разработке теории шариков. Они также разработали эффективные алгоритмы преобразования sharlet [4], как и Häuser и Steidl [6]. ShearLab [5] предоставляет обширный набор алгоритмов для обработки двух- и трехмерных данных с помощью sharlets.
Как и вейвлеты, комплексная теория связывает непрерывное преобразование sharlet с дискретным преобразованием. Кроме того, существует структура анализа множественных решений для sharlets. Как предполагает название, широты имеют примечательную особенность использования ножниц, а не вращений, для управления направленностью чувствительности. Эта характеристика позволяет создать систему sharlet из единственного или конечного набора генерирующих функций. Среди других причин успеха широток можно назвать:
Шарики обеспечивают оптимально разреженные аппроксимации анизотропных особенностей многомерных данных.
Существуют как компактно поддерживаемые, так и бандитизированные шиарки.
Преобразования Shearlet имеют эффективные алгоритмические реализации.
Подобно вейвлетам, широты не имеют уникальной системы. Операции расширения, сдвига и перемещения генерируют шарошки. Расширение может быть выражено в виде матрицы, 1/2), a∈ℝ+. Сдвиг может быть выражен (1s01), где s∈ℝ. Переменная s параметризует ориентации.
Если функция ) удовлетворяет определенным условиям (допустимости), то набор функций
{
представляет собой непрерывную систему ножниц, где а и s определены, как отмечено ранее, и
При соответствующей дискретизации параметров расширения, сдвига и перемещения получается дискретная система сдвига:
j,k∈ℤ,m∈ℤ2}.
Функция shearletSystem создает адаптированную к конусу бандитированную систему ножниц. Осуществление shearletSystem функция соответствует подходу, описанному в Häuser и Steidl [6]. Система sharlet является примером кадра, который можно нормализовать для создания кадра Parseval. Дискретное преобразование створок функции ) является внутренним произведением f со всеми стволами в дискретной системе створок k, m 〉 ∈ℤ×ℤ×ℤ2 . Вы используетеsheart2 чтобы принять дискретное преобразование sharlet изображения. Дополнительные сведения см. в разделе Ссылки.
На следующем рисунке показано, как адаптированная к конусу шарошечная система разделяет 2-D частотную плоскость. На изображении слева изображена перегородка адаптированной к конусу реально значимой системы шашек с одной шкалой. Область R в центре является низкопроходной частью системы. Кроме того, изображение включает в себя горизонтальную коническую шашлычную (симметричную по частоте, потому что она имеет действительное значение) и вертикальную коническую шашлычную. На изображении справа изображена система с тремя шкалами. Веерообразный узор придает системе шарошек свою чувствительность к направлению. Следует отметить, что число коэффициентов сдвига увеличивается по мере увеличения частотной поддержки ножницы. Когда поддержка в частотной области увеличивается, поддержка в пространственной области уменьшается.
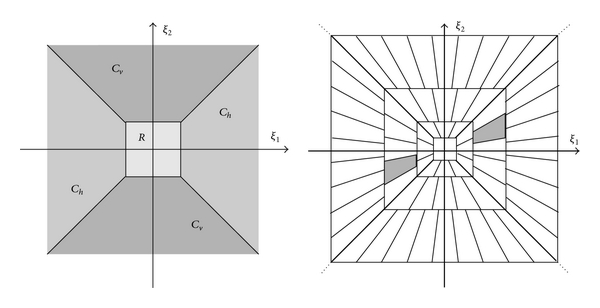
Спектры вещественнозначных шарообразных элементов одинаковы по положительному и отрицательному по сравнению с положительными и отрицательными по отношению к ним. Створки в сложных системах створок разделяются по отдельности, а не парами.
Широты являются либо вещественными, либо комплексными в пространственной области. Тип преобразования задается при использовании shearletSystem для создания системы. Вещественнозначные шарики имеют двусторонние частотные спектры. Преобразования Фурье сложнозначных шариков имеют поддержку только на половине 2-D частотного пространства. Преобразования Фурье обоих типов широт реально ценятся.
[1] Го, К., Г. Кутыниок и Д. Лабате. «Разреженные многомерные представления с использованием анизотропных операторов расширения и сдвига». Вейвлетс и сплайны: Афины 2005 (Г. Чен, и М.-Дж. Чен, ред.), 189-201. Брентвуд, TN: Nashboro Press, 2006.
[2] Го, К. и Д. Лабате. «Оптимально разреженное многомерное представление с помощью разделителей». Журнал SIAM по математическому анализу. Том 39, номер 1, 2007, стр. 298-318.
[3] Kutyniok, G. и W.-Q Lim. «Компактно поддерживаемые ножницы оптимально разрежены». Журнал теории аппроксимаций. т. 163, № 11, 2011, с. 1564-1589.
[4] Shearlets: многомасштабный анализ многомерных данных (G. Kutyniok, и D. Labate, eds.). Нью-Йорк: Спрингер, 2012.
[5] ShearLab. https://www3.math.tu-berlin.de/numerik/www.shearlab.org/.
[6] Хяузер, С. и Г. Штейдль. «Fast Finite Shearlet Transform: учебное пособие». arXiv preprint arXiv:1202.1773 (2014).
[7] Резейлуйе, Х., А. Моллахоссейни и М. Махур. «Структура классификации микроскопических медицинских изображений посредством глубокого обучения и преобразования sharlet». Журнал медицинской визуализации. Том 3, номер 4, 044501, 2016. doi:10.1117/1.JMI.3.4.044501.
isheart2 | shearletSystem | sheart2