Системы координат позволяют вам отслеживать положение самолета или космического аппарата и ориентацию в пространстве. Aerospace Blockset™ основаны на этих базовых концепциях геодезии, астрономии и физики.
Библиотека использует right-handed (RH) Cartesian систем координат. Правое правило устанавливает x - y - z последовательность координатных осей.
inertial frame является неакселерационной системой координат движения. В инерционной системе координат второй закон Ньютона содержит: сила = масса x ускорение. Неявно говоря, ускорение задано относительно далекого космоса, и инерционная система координат часто называется неакселерационной относительно неподвижных звёзд. Поскольку Земля и звезды движутся так медленно друг относительно друга, это предположение является очень точным приближением.
Строго заданная, инерционная система координат является представителем множества всех систем координат, не ускоряющихся относительно друг друга. Неинерционная система координат является любой системой координат, ускоряющейся относительно инерционной системы координат. Его ускорение, в целом, включает как поступательные так и вращательные компоненты, приводя к pseudoforces (pseudogravity,, а также Coriolis и centrifugal forces).
Библиотека моделирует форму Земли (geoid) как облатный сфероид, особый тип эллипсоида с двумя более длинными осями равными (определяющими equatorial plane) и третьей, несколько более короткой (geopolar) осью симметрии. Экватор является пересечением экваториальной плоскости и поверхности Земли. Географические полюса являются пересечением поверхности Земли и геополярной оси. В целом геополярность Земли и оси вращения не идентичны.
Широты параллельны экватору. Долготы параллельны геополярной оси. zero longitude или prime meridian проходит через Гринвич, Англия.
Библиотека делает три стандартных приближения в определении систем координат относительно Земли.
Земная поверхность или геоид представляет собой косой сфероид, заданный своими более длинными экваториальными и более короткими геополярными осями. В действительности Земля слегка деформирована относительно стандартного геоида.
Ось вращения Земли и экваториальная плоскость перпендикулярны, так что вращение и геополярные оси идентичны. В действительности эти оси слегка рассогласованы, и экваториальная плоскость колеблется, когда Земля вращается. Этот эффект незначителен в большинстве приложений.
Единственный неинерционный эффект в фиксированных Землей координатах обусловлен вращением Земли вокруг своей оси. Это rotating, geocentric система. Библиотека игнорирует ускорение Земли вокруг Солнца, ускорение Солнца в Галактике и ускорение Галактики через космос. В большинстве применений имеет значение только вращение Земли.
Это приближение должно быть изменено для космических аппаратов, отправленных в глубокое пространство, таких как вне системы Земля-Луна, и предпочтительна гелиоцентрическая система.
Библиотека использует стандартный геоид WGS-84 для моделирования Земли. Можно изменить длину экваториальной оси, уплощение и скорость вращения.
Можно представлять движение космического аппарата относительно любого небесного тела, которое хорошо аппроксимируется облатным сфероидом путем изменения размера сфероида, уплощения и скорости вращения. Если небесное тело вращается на запад (задним числом), делайте скорость вращения отрицательной.
Моделирование самолета и космического аппарата проще всего, если вы используете систему координат, фиксированную в самом теле. В случае самолета направление вперед изменяется наличием ветра, и движение судна через воздух не совпадает с его движением относительно земли.
Смотрите Уравнения Движения для получения дополнительной информации о том, как библиотека реализует координаты тела и ветра.
Неинерционная система координат тела фиксируется как в источник, так и в ориентации к движущемуся судну. Судно принято жестким.
Ориентация координатных осей тела фиксируется в форме тела.
Ось x указывает через нос аппарата.
Ось y указывает справа от оси x (обращенная в направлении зрения пилота), перпендикулярно оси x.
Ось z указывает вниз через дно судна, перпендикулярно плоскости xy и удовлетворяющей правилу RH.
Перемещения определяются перемещением вдоль этих осей расстояниями x, y и z от источника.
Повороты заданы углами Эйлера P, Q, R или Это:
| P или | Вращайте вокруг оси x |
| Q или | Тангаж вокруг оси y |
| R или | Рыскать о оси z |
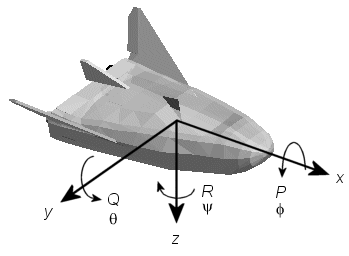
Если не указано иное, по умолчанию программа использует порядок поворота ZYX для углов Эйлера.
Неинерционная система координат ветра имеет свой источник, фиксированное в твердом самолете. Ориентация системы координат определяется относительно рабочего V скорости.
Ориентация осей координат ветра фиксируется скоростью V.
Ось x указывает в направлении V.
Ось y указывает справа от оси x (обращенная в направлении V), перпендикулярно оси x.
Ось z указывает перпендикулярно плоскости xy любым способом, необходимым для удовлетворения правила RH относительно осей x - и y -.
Перемещения определяются перемещением вдоль этих осей расстояниями x, y и z от источника.
Повороты заданы углами Эйлера
| Φ | Угол наклона вокруг оси x |
| γ | Угол тангажа вокруг оси y |
| χ | Угол рыскания вокруг оси z |
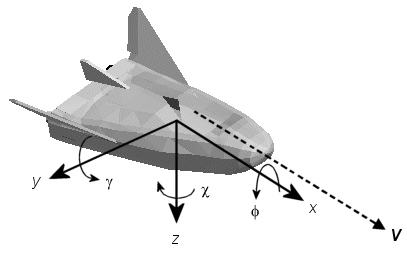
Если не указано иное, по умолчанию программа использует порядок поворота ZYX для углов Эйлера.
Моделирование аэрокосмических траекторий требует позиционирования и ориентации самолета или космического аппарата относительно вращающейся Земли. Навигационные координаты заданы относительно центра и поверхности Земли.
Значение geocentric latitude на поверхности Земли определяется углом, подчиненным вектору радиуса от центра Земли до точки поверхности с экваториальной плоскостью.
geodetic latitude w на поверхности Земли определяется углом, субтравмированным вектору нормали поверхности n и экваториальной плоскости.
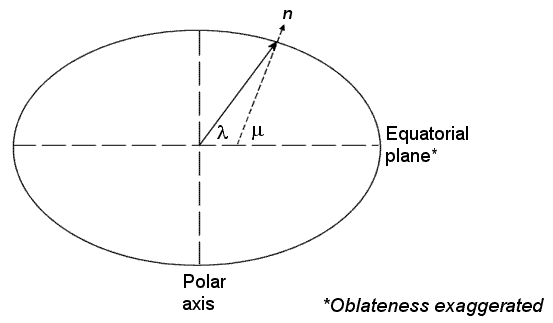
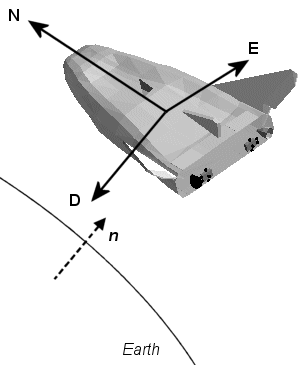
Система северо-восточного падения (NED) является неинерционной системой с источником, фиксированной в центре тяжести самолета или космического аппарата. Его оси ориентированы вдоль геодезических направлений, заданных земной поверхностью.
Ось x указывает на север параллельно геоидной поверхности в полярном направлении.
Ось y указывает на восток параллельно геоидной поверхности вдоль кривой широты.
Ось z указывает вниз, к поверхности Земли, антипараллельно к поверхности наружу от нормальной n.
Полет на постоянной высоте означает полет на постоянной z над поверхностью Земли.
Ориентированная на Землю инерционная система (ECI) не вращается. Для большинства приложений предположим, что эта система координат является инерционной, хотя равноденственная и экваториальная плоскости перемещаются очень немного с течением времени. Система ECI считается действительно инерционной для высокоточных вычислений орбиты, когда экватор и равноденствие заданы в конкретную эпоху (например, J2000). Аэрокосмические функции и блоки, которые используют конкретную реализацию системы координат ECI, предоставляют эту информацию в своей документации. Система ECI источника закреплена в центре Земли (см. рисунок).
Ось x указывает на весеннее равноденствие (First Point of Aries ♈).
Ось y указывает 90 степени к востоку от оси x в экваториальной плоскости.
Ось z указывает на север вдоль оси вращения Земли.
Координаты, ориентированные на Землю
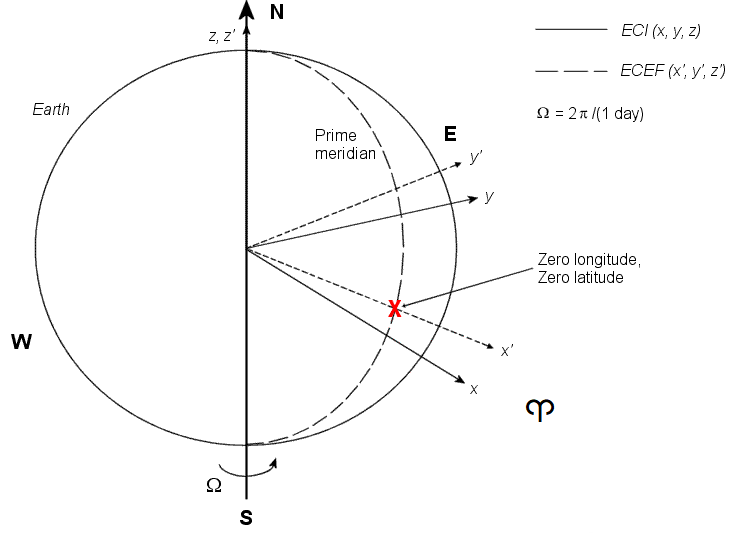
Система Earth-center, Earth-fixed (ECEF) является неинерционной и вращается вместе с Землей. Его источник фиксируется в центре Земли (см. предыдущий рисунок).
x ′ -ось указывает на пересечение экваториальной плоскости Земли и меридиана Гринвича.
y ′ -ось указывает 90 степени к востоку от оси x "-в экваториальной плоскости.
Ось z ′ указывает на север вдоль оси вращения Земли.
Несколько инструментов отображения доступны для использования с продуктом Aerospace Blockset. Каждый имеет определенную систему координат для тонирования движения.
Дополнительные сведения о MATLAB см. в разделе Внешний вид осей® Графические оси координат.
MATLAB Graphics использует эту ориентацию оси координат по умолчанию:
Ось x указывает за пределы экрана.
Ось y указывает вправо.
Ось z указывает вверх.
FlightGear является симулятором сторонних рейсов с открытым исходным кодом и интерфейсом, поддерживаемым библиотекой.
Работа с Интерфейсом Flight Simulator обсуждает интерфейс blockset к FlightGear.
См. документацию FlightGear по адресу www.flightgear.org для получения полной информации об этом симуляторе рейса.
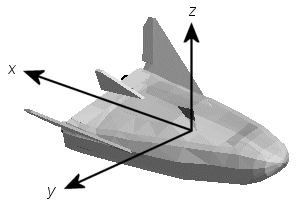
Координаты FlightGear образуют специальную систему фиксированных тел, повернутую от стандартной системы координат тел вокруг оси Y на -180 степени:
Ось x положительная к задней части транспортного средства.
Ось y положительная справа от транспортного средства.
Ось z положительная вверх, например, колеса обычно имеют самые низкие z значения.
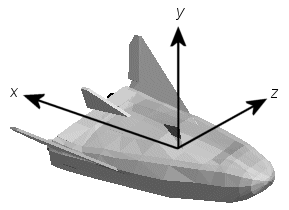
AC3D является недорогим, широко используемым редактором геометрии, доступным от https://www.inivis.com/. Его фиксированные по телу координаты формируются путем инвертирования трех стандартных осей координат тела:
Ось x положительная к задней части транспортного средства.
Ось y положительная вверх, например, колеса обычно имеют самые низкие y значения.
Ось z положительная слева от транспортного средства.
[1] Рекомендуемая практика для атмосферных и космических систем координат летательного транспортного средства, R-004-1992, ANSI/AIAA, февраль 1992 года.
[2] Rogers, R. M., Applied Mathematics in Integrated Navigation Systems, AIAA, Reston, Virginia, 2000.
[3] Sobel, D., Longitude, Walker & Company, Нью-Йорк, 1995.
[4] Stevens, B. L., and F. L. Lewis, Aircraft Control and Simulation, 2nd ed., Aircraft Control and Simulation, Wiley-Interscience, New York, 2003.
[5] Thomson, W. T., Introduction to Space Dynamics, John Wiley & Sons, New York, 1961/Dover Publications, Mineola, New York, 1986.