Проектируйте сервопривод LQR- Контроллера в Simulink

Следующий рисунок показывает Simulink^® блок показывает задачу отслеживания при проекте автопилота самолета. Чтобы открыть эту схему, введите lqrpilot в MATLAB^® приглашение.

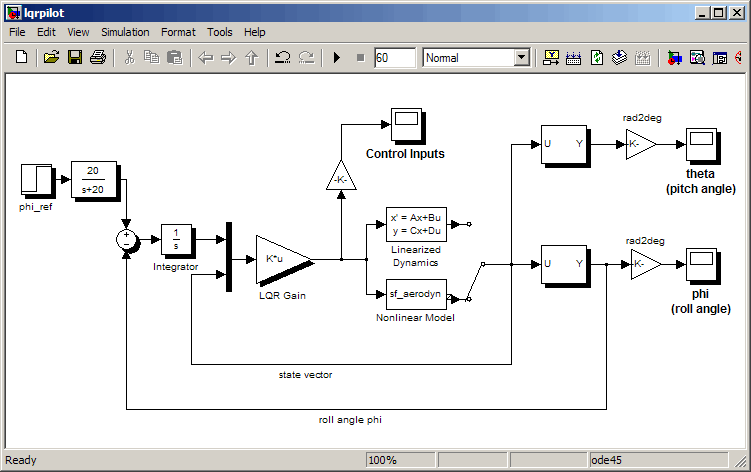
Ниже перечислены ключевые возможности этой схемы:

Блок Linearized Dynamics содержит линеаризированный планер.
sf_aerodyn является блоком S-Function, который содержит нелинейные уравнения для $(θ, ϕ) = (0, 15^{\circ})$ .
Сигнал ошибки между $ϕ$ и $ϕ_{r e f}$ передается через интегратор. Это помогает довести ошибку до нуля.

Уравнения пространства состояний для планера

Начиная со стандартного уравнения пространства состояний

$\dot{x} = A x + B u$

где

$x = {[u, v, w, p, q, r, θ, ϕ]}^{T}$

Переменные u, v и w являются тремя скоростями относительно каркаса кузова, показанными следующим образом.

Координатная система координат тела для самолета

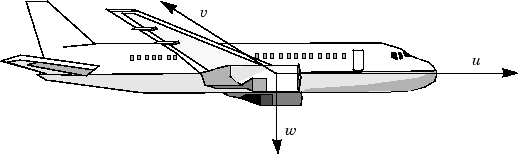
Переменные $ϕ$ и $θ$ являются скорости крена и тангажа, а p, q и r являются скоростями крена, тангажа и рыскания, соответственно.

Динамика планера нелинейна. Следующее уравнение показывает нелинейные компоненты, добавленные к уравнению пространства состояний.

Нелинейная составляющая уравнения пространства состояний

$\dot{x} = A x + B u + [\begin{matrix} - g \sin θ \\ g \cos θ \sin ϕ \\ g \cos θ \cos ϕ \\ 0 \\ 0 \\ 0 \\ q \cos ϕ - r \sin ϕ \\ (q \sin ϕ + r \cos ϕ) \cdot \tan θ \end{matrix}]$

Чтобы увидеть числовые значения для A и B, введите

load lqrpilot
A, B

в подсказку MATLAB.

Сокращение

В целях проекта LQG нелинейная динамика обрезается $ϕ = 15^{\circ}$ и p, q, r и θ равны нулю. Поскольку u, v и w не входят в нелинейный термин на предыдущем рисунке, это эквивалентно линеаризации вокруг $(θ, ϕ) = (0, 15^{\circ})$ со всеми оставшимися состояниями в нуле. Получившаяся матрица состояний линеаризированной модели называется A15.

Описание задачи

Цель выполнить устойчивый скоординированный поворот, как показано на этом рисунке.

Самолет делает поворот на 60 °

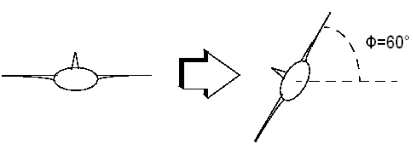
Чтобы достичь этой цели, вы должны спроектировать контроллер, который командует устойчивым поворотом, проходя через крен 60 °. В сложение примите, что θ, угол тангажа, необходим, чтобы держаться как можно ближе к нулю.

Результаты

Чтобы вычислить матрицу усиления LQG, K, type

lqrdes

в подсказку MATLAB. Затем запустите lqrpilot модель с нелинейной моделью, sf_aerodyn, выбран.

Этот рисунок показывает реакцию $ϕ$ к команде 60 ° step.

Отслеживание команды Roll Step

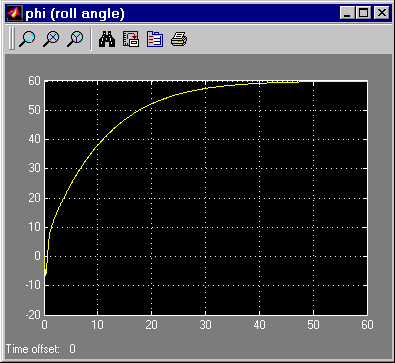
Как видим, система отслеживает командный крен на 60 ° примерно за 60 секунд.

Другой целью было сохранить θ, угол тангажа, относительно небольшой. Этот рисунок показывает, насколько хорошо это сделал контроллер LQG.

Минимизация смещения в угле тангажа, Theta

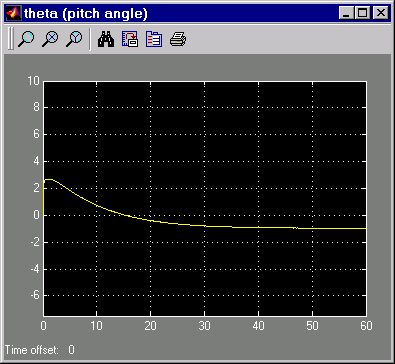
Наконец, этот рисунок показывает входы управления.

Управляйте входами для задачи отслеживания LQG

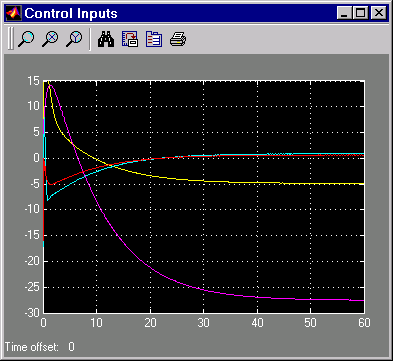
Попробуйте настроить Q и R матрицы в lqrdes.m и проверка входов управления и состояний системы, обеспечение повторного запуска lqrdes для обновления матрицы усиления LQG K. С помощью проб и ошибок вы можете улучшить время отклика этого проекта. Кроме того, сравните линейный и нелинейный проекты, чтобы увидеть эффекты нелинейности на производительности системы.

Документация