В качестве примера проекту LQG рассмотрим следующую задачу регулирования.
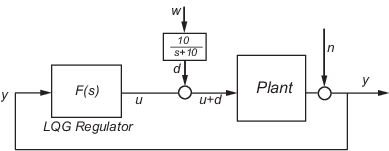
Цель состоит в том, чтобы регулировать производительность объекта y около нуля. Входное d нарушения порядка является низкой частотой с спектральной плотностью степени (PSD), сконцентрированной ниже 10 рад/с. Для целей проекта LQG он моделируется как белый шум, приводящий в действие lowpass с отключением со скоростью 10 рад/с, показанным на следующем рисунке.
![]()
Для простоты этот шум моделируется как Гауссов белый шум с отклонением 1.
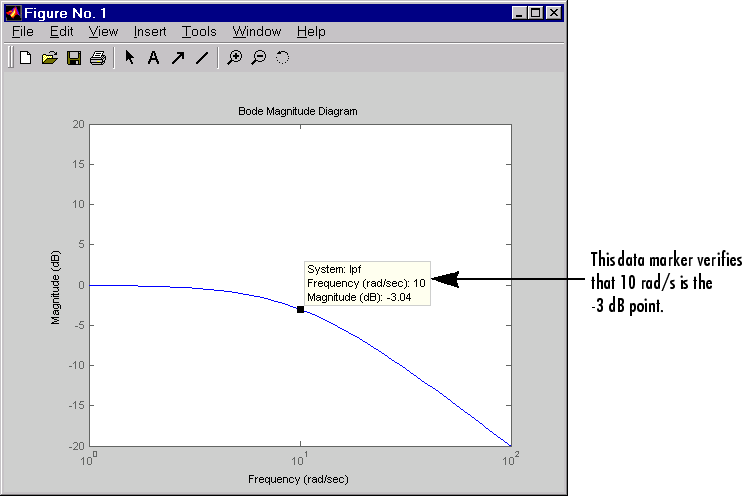
Следующий рисунок показывает величину Bode формирующего фильтра.
Базовая величина Lowpass
Существует некоторое n шума измерения с интенсивностью шума, заданной
Используйте функцию затрат
определить компромисс между эффективностью регулирования и стоимостью контроля. Следующие уравнения представляют модель пространства состояний без разомкнутого контура:
где (A, B, C) является реализацией в пространстве состояний .
Следующие команды проектируют оптимальный регулятор LQG F (s) для этой задачи:
sys = ss(tf(100,[1 1 100])) % State-space plant model % Design LQ-optimal gain K K = lqry(sys,10,1) % u = -Kx minimizes J(u) % Separate control input u and disturbance input d P = sys(:,[1 1]); % input [u;d], output y % Design Kalman state estimator Kest. Kest = kalman(P,1,0.01) % Form LQG regulator = LQ gain + Kalman filter. F = lqgreg(Kest,K)
Эти команды возвращают модель пространства состояний F регулятора LQG F (s). The lqry, kalman, и lqgreg функции выполняют проекты LQG в дискретном времени, когда вы применяете их к дискретным объектам.
Чтобы подтвердить проект, закройте цикл с помощью feedback, создайте и добавьте lowpass последовательно с системой с обратной связью и сравните импульсные характеристики разомкнутого и замкнутого контуров при помощи impulse функция.
% Close loop
clsys = feedback(sys,F,+1)
% Note positive feedback.
% Create the lowpass filter and add it in series with clsys.
s = tf('s');
lpf= 10/(s+10) ;
clsys_fin = lpf*clsys;
% Open- vs. closed-loop impulse responses
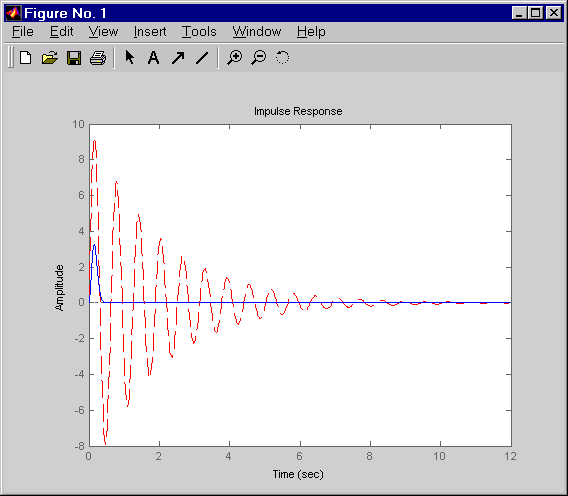
impulse(sys,'r--',clsys_fin,'b-')
Эти команды выдают следующий рисунок, которая сравнивает импульсные характеристики в разомкнутом и замкнутом циклах для этого примера.
Сравнение импульсной характеристики в разомкнутом и замкнутом контурах