Контроль за «линейным квадратным гауссовским» (LQG) - современный метод пространства состояний для проектирования оптимальных динамических регуляторов и контроллеров сервомотора с составным действием (также известный как шпионы заданного значения). Этот метод позволяет вам компромиссировать эффективность регулятора/трекера и усилия по управлению, и учитывать нарушения порядка процесса и шум измерения.
Чтобы проектировать регуляторы LQG и трекеры уставок, вы выполняете следующие шаги:
Создайте LQ-оптимальный коэффициент усиления.
Создайте фильтр Калмана (оценка состояния).
Сформируйте проект LQG путем подключения LQ-оптимального усиления и фильтра Калмана.
Для получения дополнительной информации об использовании проекта LQG для создания регуляторов LQG, смотрите проект Linear-Quadratic-Gaussian (LQG) для регулирования.
Для получения дополнительной информации об использовании проекта LQG для создания сервоприводов LQG, смотрите Linear-Quadratic-Gaussian (LQG) Design of Servo Controller with Integral Action.
Эти темы посвящены делу непрерывного времени. Для получения информации о конструкции LQG в дискретном времени смотрите dlqr и kalman страницы с описанием.
Можно спроектировать регулятор LQG, чтобы регулировать выходную y около нуля в следующей модели.
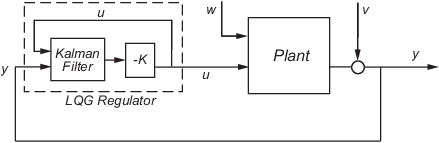
Объект в этой модели испытывает нарушения порядка (шум процесса) w и управляется u управления. Регулятор полагается на шумные измерения, y для генерации этих органов управления. Состояние объекта и уравнения измерения принимают форму
и оба w и v моделируются как белый шум.
Примечание
Проект LQG требует пространственной модели объекта. Вы можете использовать ss для преобразования других форматов модели в пространство состояний.
Для разработки регуляторов LQG можно использовать методы проектирования, показанные в следующей таблице.
| Чтобы спроектировать регулятор LQG, используя... | Используйте следующие команды: |
|---|---|
|
Быстрый, одношаговый метод проекта, когда следующее верно:
| lqg |
|
Более гибкий, трехэтапный метод проектирования, позволяющий задавать:
|
Для получения дополнительной информации см.
|
Вы создаете LQ-оптимальный коэффициент усиления из следующих элементов:
Чтобы создать оптимальный коэффициент усиления, введите следующую команду:
K= lqr(A,B,Q,R,N)
Эта команда вычисляет оптимальную матрицу усиления K, для которого закон обратной связи штата минимизирует следующую квадратичную функцию затрат на непрерывное время:
Программа вычисляет K матрицы усиления путем решения алгебраического уравнения Риккати.
Для получения информации о построении LQ-оптимального усиления, включая функцию затрат, которую программное обеспечение минимизирует для дискретного времени, смотрите lqr страница с описанием.
Вам нужен оценщик состояния Калмана для регулирования LQG и сервоуправления, потому что вы не можете реализовать оптимальную обратную связь LQ-оптимального состояния без полного измерения состояния.
Вы создаете оценку состояния таким, что остается оптимальным для задачи обратной связи на выходе. Вы создаете коэффициент усиления Кальмана из следующих элементов:
Примечание
Вы создаете оценку состояния Калмана таким же образом и для регулирования, и для сервоуправления.
Чтобы создать оценку состояния Калмана, введите следующую команду:
[kest,L,P] = kalman(sys,Qn,Rn,Nn);
Эта команда вычисляет оценку состояния Калмана, kest следующими уравнениями объекта:
где w и v моделируются как белый шум. L - коэффициент усиления и P Калмана ковариационная матрица.
Программное обеспечение генерирует эту оценку состояния с помощью фильтра Калмана
с входами u (управляет) и y (измерения). Данные о ковариации шума
определяет L усиления Калмана посредством алгебраического уравнения Риккати.
Фильтр Калмана является оптимальным оценщиком при работе с Гауссовым белым шумом. В частности, это минимизирует асимптотическую ковариацию
от ошибки расчета .
![]()
Для получения дополнительной информации смотрите kalman страница с описанием. Полный пример реализации фильтра Калмана см. в разделе Фильтрация Калмана.
Для формирования регулятора LQG подключите фильтр Калмана kest и LQ-оптимальный коэффициент усиления K путем ввода следующей команды:
regulator = lqgreg(kest, K);
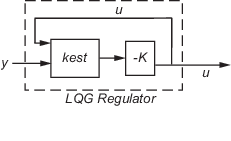
Регулятор имеет следующие уравнения пространства состояний:
Для получения дополнительной информации о формировании регуляторов LQG смотрите lqgreg и Правила LQG: Пример прокатного стана.
Вы можете проектировать контроллер сервомотора с составным действием для следующей модели:

Проектируемый сервоконтроллер гарантирует, что выходной y отслеживает опорную командную r при отклонении технологических возмущений w и шумовых v измерения.
Объект на предыдущем рисунке подвержен нарушениям порядка w и управляется u управления. Контроллер сервопривода полагается на шумные измерения, y, чтобы сгенерировать эти элементы управления. Состояние объекта и уравнения измерения имеют вид
и оба w и v моделируются как белый шум.
Примечание
Проект LQG требует пространственной модели объекта. Вы можете использовать ss для преобразования других форматов модели в пространство состояний.
Для разработки сервоприводов LQG можно использовать методы проектирования, показанные в следующей таблице.
| Чтобы спроектировать сервопривод LQG контроллера используя... | Используйте следующие команды: |
|---|---|
|
Быстрый, одношаговый метод проекта, когда следующее верно:
| lqg |
|
Более гибкий, трехэтапный метод проектирования, позволяющий задавать:
|
Для получения дополнительной информации см.
|
Вы создаете LQ-оптимальный коэффициент усиления из
Пространство состояний модели объекта управления sys
Матрицы взвешивания Q, R, и N, которые определяют компромисс между эффективностью трекера и усилиями по управлению
Чтобы создать оптимальный коэффициент усиления, введите следующую команду:
K= lqi(sys,Q,R,N)
Эта команда вычисляет оптимальную матрицу усиления K, для которого закон обратной связи штата минимизирует следующую квадратичную функцию затрат на непрерывное время:
Программа вычисляет K матрицы усиления путем решения алгебраического уравнения Риккати.
Для получения информации о построении LQ-оптимального усиления, включая функцию затрат, которую программное обеспечение минимизирует для дискретного времени, смотрите lqi страница с описанием.
Вам нужен оценщик состояния Калмана для регулирования LQG и сервоуправления, потому что вы не можете реализовать обратную связь LQ-оптимального состояния без полного измерения состояния.
Вы создаете оценку состояния таким, что остается оптимальным для задачи обратной связи на выходе. Вы создаете коэффициент усиления Кальмана из следующих элементов:
Примечание
Вы создаете оценку состояния Калмана таким же образом и для регулирования, и для сервоуправления.
Чтобы создать оценку состояния Калмана, введите следующую команду:
[kest,L,P] = kalman(sys,Qn,Rn,Nn);
Эта команда вычисляет оценку состояния Калмана, kest следующими уравнениями объекта:
где w и v моделируются как белый шум. L - коэффициент усиления и P Калмана ковариационная матрица.
Программное обеспечение генерирует эту оценку состояния с помощью фильтра Калмана
с входами u (управляет) и y (измерения). Данные о ковариации шума
определяет L усиления Калмана посредством алгебраического уравнения Риккати.
Фильтр Калмана является оптимальным оценщиком при работе с Гауссовым белым шумом. В частности, это минимизирует асимптотическую ковариацию
от ошибки расчета .
![]()
Для получения дополнительной информации смотрите kalman страница с описанием. Полный пример реализации фильтра Калмана см. в разделе Фильтрация Калмана.
Для формирования сервопривода LQG с двумя степенями свободы подключите фильтр Калмана kest и LQ-оптимальный коэффициент усиления K путем ввода следующей команды:
servocontroller = lqgtrack(kest, K);
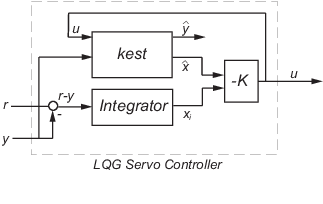
Сервопривод контроллера имеет следующие уравнения пространства состояний:
Для получения дополнительной информации о формировании сервоприводов LQG, в том числе о том, как сформировать сервопривод LQG с одной степенью свободы, смотрите lqgtrack страница с описанием.
kalman | lqg | lqgreg | lqgtrack | lqi | lqr