kalman

Проект фильтра Калмана для оценки состояния

Свернуть все на странице

Синтаксис

[kalmf,L,P] = kalman(sys,Q,R,N)

[kalmf,L,P] = kalman(sys,Q,R,N,sensors,known)

[kalmf,L,P,Mx,Z,My] = kalman(___)

[kalmf,L,P,Mx,Z,My] = kalman(___,type)

Описание

пример

[kalmf,L,P] = kalman(sys,Q,R,N) создает фильтр Калмана, заданный для модели объекта управления sys и данные о шумовой ковариации Q, R, и N. Функция вычисляет фильтр Калмана для использования в Оценку состояния фильтра Калмана со строения, показанной на следующей схеме.

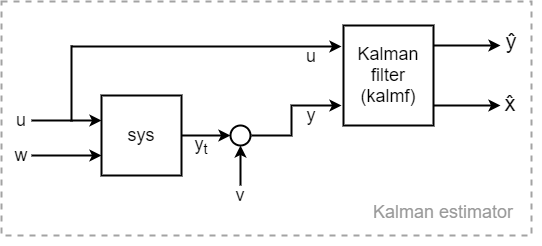
Kalman estimator including plant sys and Kalman filter kalmf. The plant has input u, noise input w, and output yt. The Kalman filter takes as inputs w and noisy plant output y = yt + v. The filter outputs are y-hat, the estimated true plant output, and x-hat, the estimated state values.

Вы создаете модель sys с известными входами u и белыми входами w шума процесса, так что w состоит из последних входов _Nw, чтобы sys. Выходной _yt «объекта состоит из всех выходов sys. Вы также предоставляете шумовые ковариационные данные Q, R, и N. Возвращенный фильтр Калмана kalmf является моделью пространства состояний, которая принимает известные входы u и шумные измерения y и производит оценку $\hat{y}$ истинного выхода объекта и оценки $\hat{x}$ состояний объекта. kalman также возвращает коэффициент усиления Калмана L и установившуюся ковариационную матрицу ошибок P.

пример

[kalmf,L,P] = kalman(sys,Q,R,N,sensors,known) вычисляет фильтр Калмана, когда существует одно или оба из следующих условий.

Не все выходы sys измеряют.
Входы нарушения порядка w не являются последними входами sys.

Вектор индекса sensors определяет, какие выходы sys измеряют. Эти выходы составляют y. Вектор индекса known определяет, какие входы известны (детерминированные). Известные входы составляют u. The kalman команда принимает оставшиеся входы sys быть стохастическими входами w.

[kalmf,L,P,Mx,Z,My] = kalman(___) также возвращает преимущества инноваций Mx и My и установившиеся ковариации ошибок P и Z для дискретного времени sys. Можно использовать этот синтаксис с любыми предыдущими комбинациями входных аргументов.

[kalmf,L,P,Mx,Z,My] = kalman(___,type) задает тип оценщика для дискретного времени sys.

type = 'current' - Вычисление выходных оценок $\hat{y} [n | n]$ и оценки состояния $\hat{x} [n | n]$ использование всех доступных измерений до $y [n]$ .
type = 'delayed' - Вычисление выходных оценок $\hat{y} [n | n - 1]$ и оценки состояния $\hat{x} [n | n - 1]$ использование измерений только до $y [n - 1]$ . Блок отложенной оценки легче реализовать внутри циклов управления.

Можно использовать type входной параметр с любыми из предыдущих комбинаций входных аргументов.

Примеры

свернуть все

Проект фильтра Калмана для объекта SISO

Открыть Live Script

Создайте фильтр Калмана для объекта, который имеет аддитивный белый шум w на входе и v на выходе, как показано на следующей схеме.

Предположим, что объект имеет следующие матрицы пространства состояний и является объектом дискретного времени с неопределенным шагом расчета (Ts = -1).

A = [1.1269   -0.4940    0.1129 
     1.0000         0         0 
          0    1.0000         0];

B = [-0.3832
      0.5919
      0.5191];

C = [1 0 0];

D = 0;

Plant = ss(A,B,C,D,-1);
Plant.InputName = 'un';
Plant.OutputName = 'yt';

Как использовать kalman, вы должны предоставить модель sys который имеет вход для шума w. Таким образом, sys не то же самое что и Plant, потому что Plant принимает входной параметр un = u + w. Можно создавать sys путем создания суммирующего соединения для входного сигнала шума.

Sum = sumblk('un = u + w');
sys = connect(Plant,Sum,{'u','w'},'yt');

Эквивалентно, можно использовать sys = Plant*[1 1].

Задайте ковариации шума. Поскольку объект имеет один вход шума и один выход, эти значения скаляры. На практике эти значения являются свойствами источников шума в вашей системе, которые вы определяете по измерению или другим знаниям вашей системы. В данном примере предположим, что оба источника шума имеют единичную ковариацию и не коррелированы (N = 0).

Q = 1;
R = 1;
N = 0;

Проектируйте фильтр.

[kalmf,L,P] = kalman(sys,Q,R,N);
size(kalmf)

State-space model with 4 outputs, 2 inputs, and 3 states.

Фильтр Калмана kalmf является моделью пространства состояний, имеющей два входа и четыре выхода. kalmf принимает как входы входной сигнал u объекта управления и выходной выход шумного объекта $y = y_{t} + v$ . Первый выход является предполагаемым истинным выходом объекта управления $y_{}^{ˆ}$ . Оставшиеся три выхода являются оценками состояния $x_{}^{ˆ}$ . Исследуйте входные и выходные имена kalmf чтобы увидеть, как kalman подписывает их соответственно.

kalmf.InputName

ans = 2x1 cell
    {'u' }
    {'yt'}

kalmf.OutputName

ans = 4x1 cell
    {'yt_e'}
    {'x1_e'}
    {'x2_e'}
    {'x3_e'}

Исследуйте усиления Калмана L. Для объекта SISO с тремя состояниями, L является трехэлементным вектором-столбцом.

Для примера, который показывает, как использовать kalmf чтобы уменьшить ошибку измерения из-за шума, см. «Фильтрация Калмана».

Проект фильтра Калмана для объекта MIMO

Открыть Live Script

Рассмотрим объект с тремя входами, один из которых представляет шум процесса w, и двумя измеренными выходами. У объекта четыре состояния.

Принимая следующие матрицы пространства состояний, создайте sys.

A = [-0.71  0.06 -0.19 -0.17;
      0.06 -0.52 -0.03  0.30;
     -0.19 -0.03 -0.24 -0.02;
     -0.17  0.30 -0.02 -0.41];

B = [ 1.44  2.91   0;
     -1.97  0.83 -0.27;
     -0.20  1.39  1.10;
     -1.2   0    -0.28];

C = [ 0    -0.36 -1.58 0.28;
     -2.05  0     0.51 0.03];

D = zeros(2,3);

sys = ss(A,B,C,D);
sys.InputName = {'u1','u2','w'};
sys.OutputName = {'y1','y2'};

Поскольку объект имеет только один вход технологического шума, ковариация Q является скаляром. В данном примере предположим, что шум процесса имеет единичную ковариацию.

Q = 1;

kalman использует размерности Q для определения, какие входы известны, а какие являются шумовыми входами. Для скалярных Q, kalman принимает один входной параметр шума и использует последний вход, если вы не задаете обратное (см. «Объект с неизмеренными выходами»).

Для шума измерения на двух выходах задайте шумовую ковариационную матрицу 2 на 2. В данном примере используйте отклонение модулей для первого выхода и отклонение 1,3 для второго выхода. Установите значения вне диагонали на нуль, чтобы указать, что два канала шума являются некоррелированными.

R = [1 0;
     0 1.3];

Проектируйте фильтр Калмана.

[kalmf,L,P] = kalman(sys,Q,R);

Исследуйте входы и выходы. kalman использует InputName, OutputName, InputGroup, и OutputGroup свойства kalmf чтобы помочь вам отслеживать, какие входы и выходы kalmf представляют.

kalmf.InputGroup

ans = struct with fields:
     KnownInput: [1 2]
    Measurement: [3 4]

kalmf.InputName

ans = 4x1 cell
    {'u1'}
    {'u2'}
    {'y1'}
    {'y2'}

kalmf.OutputGroup

ans = struct with fields:
    OutputEstimate: [1 2]
     StateEstimate: [3 4 5 6]

kalmf.OutputName

ans = 6x1 cell
    {'y1_e'}
    {'y2_e'}
    {'x1_e'}
    {'x2_e'}
    {'x3_e'}
    {'x4_e'}

Таким образом, два известных входов u1 и u2 являются первыми двумя входами kalmf и два измеренных выхода y1 и y2 являются ли последние два входов kalmf. Для выходов kalmfпервые два являются предполагаемыми выходами, а остальные четыре - оценками состояния. Чтобы использовать фильтр Калмана, соедините эти входы с объектом и шумовые сигналы способом, подобным показанному для объекта SISO в Kalman Filtering.

Объект с неизмеренными выходами

Открыть Live Script

Рассмотрим объект с четырьмя входами и двумя выходами. Первый и третий входы известны, в то время как второй и четвертый входы представляют шум процесса. У объект также есть два выхода, но измеряется только второй из них.

Используйте следующие матрицы пространства состояний, чтобы создать sys.

A = [-0.37  0.14 -0.01  0.04;
     0.14 -1.89  0.98 -0.11;
    -0.01  0.98 -0.96 -0.14;
     0.04 -0.11 -0.14 -0.95];

B = [-0.07 -2.32  0.68  0.10;
     -2.49  0.08  0     0.83;
      0    -0.95  0     0.54;
     -2.19  0.41  0.45  0.90];

C = [ 0     0    -0.50 -0.38;
     -0.15 -2.12 -1.27  0.65];

D = zeros(2,4);

sys = ss(A,B,C,D,-1);    % Discrete with unspecified sample time

sys.InputName = {'u1','w1','u2','w2'};
sys.OutputName = {'yun','ym'};

Как использовать kalman для разработки фильтра для этой системы используйте known и sensors входные аргументы для определения, какие входы для объекта управления известны и какие выходные параметры измеряются.

known = [1 3];
sensors = [2];

Задайте шумовые ковариации и спроектируйте фильтр.

Q = eye(2);
R = 1;
N = 0;

[kalmf,L,P] = kalman(sys,Q,R,N,sensors,known);

Изучение входа и выхода меток kalmf показывает входы, которые ожидает фильтр, и выходы, которые он возвращает.

kalmf.InputGroup

ans = struct with fields:
     KnownInput: [1 2]
    Measurement: 3

kalmf.InputName

ans = 3x1 cell
    {'u1'}
    {'u2'}
    {'ym'}

kalmf принимает в качестве входов два известных входов sys и шумные измеренные выходы sys.

kalmf.OutputGroup

ans = struct with fields:
    OutputEstimate: 1
     StateEstimate: [2 3 4 5]

Первый выход kalmf - его оценка истинного значения измеряемого выхода объекта. Остальные выходы являются оценками состояния.

Входные параметры

свернуть все

`sys` - Модель объекта управления с технологическим шумом
`ss` модель

Модель объекта управления с технологическим шумом, заданная как пространство состояний (ss) модель. Объект имеет известные входы u и белые входы шума процесса w. Выходные данные объекта _yt не включает шум измерения.

Diagram showing that sys includes plant dynamics and process noise inputs, but not the additive noise on the plant output.

Можно записать матрицы пространства состояний такой модели объекта управления как:

$A, [B G], C, [D H]$

kalman принимает Гауссов шум, v на выходе. Таким образом, за непрерывное время, уравнения в пространстве состояний, которые kalman работает с:

$\begin{array}{l} \dot{x} = A x + B u + G w \\ y = C x + D u + H w + v \end{array}$

В дискретном времени уравнения в пространстве состояний:

$\begin{array}{l} x [n + 1] = A x [n] + B u [n] + G w [n] \\ y [n] = C x [n] + D u [n] + H w [n] + v [n] \end{array}$

Если вы не используете known входной параметр, kalman использует размер Q определить, какие входы sys являются шумовыми входами. В этом случае, kalman обрабатывает последнюю _Nw = size(Q,1) входы как шумовые входы. Когда шум вводит w не являются последними входами sys, можно использовать known входной параметр, чтобы указать, какие входы объекта известны. kalman обрабатывает оставшиеся входы как стохастические.

Дополнительные ограничения на свойства растительных матриц см. в разделе Ограничения.

`Q` - Ковариация технологического шума
скалярная матрица |

Ковариация технологического шума, заданная как скалярная или _Nw -by - Nw матрица, где Nw - количество шумовых входов для объекта. kalman использует размер Q определить, какие входы sys являются шумовыми входами, принимая последний _Nw = size(Q,1) входы, которые будут шумовыми входами, если вы не задаете обратное со known входной параметр.

kalman принимает, что w шума процесса является Гауссовым шумом с ковариацией Q = E (ww^T). Когда объект имеет только один вход технологического шума, Q является скаляром, равным отклонению w. Когда объект имеет несколько, некоррелированных шумовых входов, Q является диагональной матрицей. На практике вы определяете соответствующие значения для Q путем измерения или создания образованных догадок о шумовых свойствах вашей системы.

`R` - Ковариация шума измерения
скалярная матрица |

Ковариация шума измерения, заданная как скалярная или _Ny -by - Ny матрица, где Ny - количество выходов объекта.kalman принимает, что измерение шумовой v является белый шум с ковариацией R = E (vv^T). Когда объект имеет только один выходной канал, R является скаляром, равным отклонению v. Когда объект имеет несколько выходных каналов с некоррелированным шумом измерения, R является диагональной матрицей. На практике вы определяете соответствующие значения для R путем измерения или создания образованных догадок о шумовых свойствах вашей системы.

Для дополнительных ограничений на ковариацию шума измерения смотрите Ограничения.

`N` - Перекрестная ковариация шума
0 (по умолчанию) | скалярную матрицу |

Перекрестная ковариация шума, заданная как скалярная или _Ny -by - Nw матрица.kalman принимает, что шум процесса w и шум измерения v удовлетворять N = E (wv^T). Если два источника шума не коррелированы, можно опустить N, что эквивалентно установке N = 0. На практике вы определяете соответствующие значения для N путем измерения или создания образованных догадок о шумовых свойствах вашей системы.

`sensors` - Измеренные выходы `sys`
вектор

Измеренные выходы sys, заданный как вектор индексов, идентифицирующих какие выходы sys измеряют. Например, предположим, что ваша система имеет три выхода, но измеряются только два из них, соответствующих первому и третьему выходам sys. В этом случае установите sensors = [1 3].

`known` - Известные входы `sys`
вектор

Известные входы sys, заданный как вектор индексов, идентифицирующих, какие входы известны (детерминированные). Например, предположим, что ваша система имеет три входа, но известны только первый и второй входы. В этом случае установите known = [1 2]. kalman интерпретирует все оставшиеся входы sys быть стохастическим.

`type` - Тип оценки в дискретном времени
`'current'` (по умолчанию) | `'delayed'`

Тип вычисляемой оценки в дискретном времени, заданный как 'current' или 'delayed'. Этот вход релевантен только для дискретного времени sys.

'current' - Вычисление выходных оценок $\hat{y} [n | n]$ и оценки состояния $\hat{x} [n | n]$ использование всех доступных измерений до $y [n]$ .
'delayed' - Вычисление выходных оценок $\hat{y} [n | n - 1]$ и оценки состояния $\hat{x} [n | n - 1]$ использование измерений только до $y [n - 1]$ . Блок отложенной оценки легче реализовать внутри циклов управления.

Для получения дополнительной информации о том, как kalman вычисляет текущую и задержанную оценки, см. «Оценка дискретного времени».

Выходные аргументы

свернуть все

`kalmf` - оценка состояния фильтра Калмана
`ss` модель

Оценка состояния фильтра Калмана или фильтр Калмана, возвращенный как пространство состояний (ss) модель. Получившаяся оценка имеет входы $[u; y]$ и выходы $[\hat{y}; \hat{x}]$ . Другими словами, kalmf принимает как входы входные u объекта управления и выходные y зашумленного объекта управления, и производит как выходные значения расчетный выход объекта без шума $\hat{y}$ и оцененные значения состояний $\hat{x}$ .

Diagram showing Kalman filter with inputs u and y and outputs y-hat and x-hat.

kalman автоматически устанавливает InputName, OutputName, InputGroup, и OutputGroup свойства kalmf чтобы помочь вам отслеживать, какие входы и выходы соответствуют каким сигналам.

Для состояния и выходных уравнений kalmf, см. Оценка в непрерывном времени и оценка в дискретном времени.

`L` - Коэффициент усиления фильтра
массив

Коэффициент усиления фильтра, возвращенный как массив размера _Nx -by - Ny, где Nx - количество состояний на заводе и Ny - количество выходов объекта. За непрерывное время уравнение состояния фильтра Калмана является:

$\dot{\hat{x}} = A \hat{x} + B u + L (y - C \hat{x} - D u) .$

В дискретном времени уравнение состояния является:

$\hat{x} [n + 1 | n] = A \hat{x} [n | n - 1] + B u [n] + L (y [n] - C \hat{x} [n | n - 1] - D u [n]) .$

Для получения дополнительной информации об этих выражениях и как L вычисляется, см. Оценка в непрерывном времени и оценка в дискретном времени.

`P`, `Z` - Ковариации статической ошибки
массив

Ковариации статической ошибки, возвращенные как _Nx -by- Nx, где Nx количество состояний на объекте. Фильтр Калмана вычисляет оценки состояния, которые минимизируют P. За непрерывное время ковариация установившейся ошибки задается:

$P = \lim_{t \to \infty} E ({x - \hat{x}} {x - \hat{x}}^{T}) .$

В дискретном времени ковариации статической ошибки задаются:

$\begin{array}{l} P = \lim_{n \to \infty} E ({x [n] - \hat{x} [n | n - 1]} {x [n] - \hat{x} [n | n - 1]}^{T}), \\ Z = \lim_{n \to \infty} E ({x [n] - \hat{x} [n | n]} {x [n] - \hat{x} [n | n]}^{T}) . \end{array}$

Для получения дополнительной информации об этих количествах и как kalman использует их, см. Оценка в непрерывном времени и Оценка в дискретном времени.

`Mx`, `My` - Инновационные достижения государственных оценщиков
массив

Инновационные усиления оценок состояний для систем дискретного времени, возвращенные как массив.

Mx и My релевантны только тогда, когда type = 'current', который является оценщиком по умолчанию для систем дискретного времени. Для непрерывных sys или type = 'delayed', затем Mx = My = [].

Для 'current' type estimator, Mx и My являются нововведениями в обновленных уравнениях:

$\hat{x} [n | n] = \hat{x} [n | n - 1] + M_{x} (y [n] - C \hat{x} [n | n - 1] - D u [n])$

$\hat{y} [n | n] = C \hat{x} [n | n - 1] + D u [n] + M_{y} (y [n] - C \hat{x} [n | n - 1] - D u [n])$

Когда нет прямого сквозного соединения от входного w шума к выходному y объекта (то есть, когда H = 0, см. Оценку дискретного времени), то $M_{y} = C M_{x}$ , и оценка выхода упрощает $\hat{y} [n | n] = C \hat{x} [n | n] + D u [n]$ .

Размерности массивов Mx и My зависят от размерностей sys следующим образом.

Mx - _Nx -by - Ny, где Nx - количество состояний на объекте и Ny - количество выходов.
My - _Ny -by - Ny.

Для получения дополнительной информации о том, как kalman получает Mx и My, см. Оценка в дискретном времени.

Ограничения

Объект и данные о шуме должны удовлетворять:

(C, A) обнаруживается, где:
$\bar{R} > 0$ и $[\begin{matrix} \bar{Q} & \bar{N}; \begin{matrix} {\bar{N}}^{'} & \bar{R} \end{matrix} \end{matrix}] \geq 0$ , где
$[\begin{matrix} \bar{Q} & \bar{N} \\ {\bar{N}}^{'} & \bar{R} \end{matrix}] = [\begin{matrix} G & 0 \\ H & I \end{matrix}] [\begin{matrix} Q & N \\ N^{'} & R \end{matrix}] {[\begin{matrix} G & 0 \\ H & I \end{matrix}]}^{'} .$
$(A - \bar{N} {\bar{R}}^{- 1} C, \bar{Q} - \bar{N} {\bar{R}}^{- 1} {\bar{N}}^{T})$ не имеет неконтролируемого режима на мнимой оси за непрерывное время или на модуль круге за дискретное время.

Алгоритмы

свернуть все

Оценка в непрерывном времени

Рассмотрим объект непрерывного времени с известными входами u, белыми w шума процесса и белыми v шума измерения:

$\begin{array}{l} \dot{x} = A x + B u + G w \\ y = C x + D u + H w + v \end{array}$

Шумовые сигналы w и v удовлетворяют:

$E (w) = E (v) = 0, E (w w^{T}) = Q, E (v v^{T}) = R, E (w v^{T}) = N$

Фильтр Калмана, или оценка состояния фильтра Калмана, вычисляет оценку состояния $\hat{x} (t)$ что минимизирует ковариацию установившейся ошибки:

$P = \lim_{t \to \infty} E ({x - \hat{x}} {x - \hat{x}}^{T}) .$

Фильтр Калмана имеет следующее состояние и выходные уравнения:

$\begin{array}{l} \frac{d \hat{x}}{d t} = A \hat{x} + B u + L (y - C \hat{x} - D u) \\ [\begin{matrix} \hat{y} \\ \hat{x} \end{matrix}] = [\begin{matrix} C \\ I \end{matrix}] \hat{x} + [\begin{matrix} D \\ 0 \end{matrix}] u \end{array}$

Чтобы получить коэффициент усиления L, kalman решает алгебраическое уравнение Риккати, чтобы получить

$L = (P C^{T} + \bar{N}) {\bar{R}}^{- 1}$

где

$\begin{array}{l} \bar{R} = R + H N + N^{T} H^{T} + H Q H^{T} \\ \bar{N} = G (Q H^{T} + N) \end{array}$

P решает соответствующее алгебраическое уравнение Риккати.

Оценщик использует известные входы u и y измерений, чтобы сгенерировать выход и оценки состояния $\hat{y}$ и $\hat{x}$ .

Оценка в дискретном времени

Дискретный объект определяется:

$\begin{array}{l} x [n + 1] = A x [n] + B u [n] + G w [n] \\ y [n] = C x [n] + D u [n] + H w [n] + v [n] \end{array}$

В дискретном времени сигналы шума w и v удовлетворяют:

$E (w [n] w {[n]}^{T}) = Q, E (v [n] v {[n]}^{T}) = R, E (w [n] v {[n]}^{T}) = N$

Оценка в дискретном времени имеет следующее уравнение состояния:

$\hat{x} [n + 1 | n] = A \hat{x} [n | n - 1] + B u [n] + L (y [n] - C \hat{x} [n | n - 1] - D u [n]) .$

kalman решает дискретное уравнение Риккати, чтобы получить L матрицы усиления:

$L = (A P C^{T} + \bar{N}) {(C P C^{T} + \bar{R})}^{- 1}$

где

$\begin{array}{l} \bar{R} = R + H N + N^{T} H^{T} + H Q H^{T} \\ \bar{N} = G (Q H^{T} + N) \end{array}$

kalman может вычислить два варианта оценки состояния фильтра Калмана в дискретном времени, текущую оценку (type = 'current') и отсроченную оценку (type = 'delayed').

Оценка тока - Генерирует выход оценки $\hat{y} [n | n]$ и оценки состояния $\hat{x} [n | n]$ использование всех доступных измерений до $y [n]$ . Эта оценка имеет выходное уравнение

$[\begin{matrix} \hat{y} [n | n] \\ \hat{x} [n | n] \end{matrix}] = [\begin{matrix} (I - M_{y}) C \\ I - M_{x} C \end{matrix}] \hat{x} [n | n - 1] + [\begin{matrix} (I - M_{y}) D & M_{y} \\ - M_{x} D & M_{x} \end{matrix}] [\begin{matrix} u [n] \\ y [n] \end{matrix}] .$
где инновационные усиления _Mx и _My определяются как:
$\begin{matrix} M_{x} = P C^{T} {(C P C^{T} + \bar{R})}^{- 1}, \\ M_{y} = (C P C^{T} + H Q H^{T} + H N) {(C P C^{T} + \bar{R})}^{- 1} . \end{matrix}$
Таким образом, _Mx обновляет оценку состояния $\hat{x} [n | n - 1]$ использование нового измерения $y [n]$ :
$\hat{x} [n | n] = \hat{x} [n | n - 1] + M_{x} (y [n] - C \hat{x} [n | n - 1] - D u [n])$
Точно так же _My вычисляет обновленную оценку выхода:
$\hat{y} [n | n] = C \hat{x} [n | n - 1] + D u [n] + M_{y} (y [n] - C \hat{x} [n | n - 1] - D u [n])$
Когда H = 0, тогда $M_{y} = C M_{x}$ , и оценка выхода упрощает $\hat{y} [n | n] = C \hat{x} [n | n] + D u [n]$ .
Отложенная оценка - Генерирует выход оценки $\hat{y} [n | n - 1]$ и оценки состояния $\hat{x} [n | n - 1]$ использование измерений только до _yv [n -1]. Этот оценщик имеет выход уравнение:

$[\begin{matrix} \hat{y} [n | n - 1] \\ \hat{x} [n | n - 1] \end{matrix}] = [\begin{matrix} C \\ I \end{matrix}] \hat{x} [n | n - 1] + [\begin{matrix} D & 0 \\ 0 & 0 \end{matrix}] [\begin{matrix} u [n] \\ y [n] \end{matrix}]$
Блок отложенной оценки легче развернуть внутри циклов управления.

Документация

kalman

Синтаксис

Описание

Примеры

Проект фильтра Калмана для объекта SISO

Проект фильтра Калмана для объекта MIMO

Объект с неизмеренными выходами

Входные параметры

`sys` - Модель объекта управления с технологическим шумом
`ss` модель

`Q` - Ковариация технологического шума
скалярная матрица |

`R` - Ковариация шума измерения
скалярная матрица |

`N` - Перекрестная ковариация шума
0 (по умолчанию) | скалярную матрицу |

`sensors` - Измеренные выходы `sys`
вектор

`known` - Известные входы `sys`
вектор

`type` - Тип оценки в дискретном времени
`'current'` (по умолчанию) | `'delayed'`

Выходные аргументы

`kalmf` - оценка состояния фильтра Калмана
`ss` модель

`L` - Коэффициент усиления фильтра
массив

`P`, `Z` - Ковариации статической ошибки
массив

`Mx`, `My` - Инновационные достижения государственных оценщиков
массив

Ограничения

Алгоритмы

Оценка в непрерывном времени

Оценка в дискретном времени

См. также

Блоки

Темы

Control System Toolbox документация

Поддержка

Документация

kalman

Синтаксис

Описание

Примеры

Проект фильтра Калмана для объекта SISO

Проект фильтра Калмана для объекта MIMO

Объект с неизмеренными выходами

Входные параметры

sys - Модель объекта управления с технологическим шумом ss модель

Q - Ковариация технологического шума скалярная матрица |

R - Ковариация шума измерения скалярная матрица |

N - Перекрестная ковариация шума 0 (по умолчанию) | скалярную матрицу |

sensors - Измеренные выходы sys вектор

known - Известные входы sys вектор

type - Тип оценки в дискретном времени 'current' (по умолчанию) | 'delayed'

Выходные аргументы

kalmf - оценка состояния фильтра Калмана ss модель

L - Коэффициент усиления фильтра массив

P, Z - Ковариации статической ошибки массив

Mx, My - Инновационные достижения государственных оценщиков массив

Ограничения

Алгоритмы

Оценка в непрерывном времени

Оценка в дискретном времени

См. также

Блоки

Темы

Control System Toolbox документация

Поддержка

`sys` - Модель объекта управления с технологическим шумом
`ss` модель

`Q` - Ковариация технологического шума
скалярная матрица |

`R` - Ковариация шума измерения
скалярная матрица |

`N` - Перекрестная ковариация шума
0 (по умолчанию) | скалярную матрицу |

`sensors` - Измеренные выходы `sys`
вектор

`known` - Известные входы `sys`
вектор

`type` - Тип оценки в дискретном времени
`'current'` (по умолчанию) | `'delayed'`

`kalmf` - оценка состояния фильтра Калмана
`ss` модель

`L` - Коэффициент усиления фильтра
массив

`P`, `Z` - Ковариации статической ошибки
массив

`Mx`, `My` - Инновационные достижения государственных оценщиков
массив