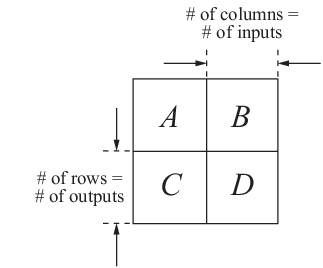
Модели пространства состояний MIMO

MIMO явные модели пространства состояний

Вы создаете модель пространства состояний MIMO так же, как и модель пространства состояний SISO. Единственное различие между случаями SISO и MIMO является размерностями матриц пространства состояний. Размерности B, C и D матриц увеличиваются с количеством входов и выходов, как показано на следующем рисунке.

В этом примере вы создаете модель пространства состояний для вращающегося тела с J тензора инерции, F демпфирующей силы и тремя осями вращения, связанными с:

$\begin{matrix} J \frac{d ω}{d t} + F ω = T \\ y = ω . \end{matrix}$

Входной T системы является приводным крутящим моментом. Выходной y является вектором скоростей вращения вращающегося тела.

Чтобы выразить эту систему в форме пространства состояний:

$\begin{matrix} \frac{d x}{d t} = A x + B u \\ y = C x + D u \end{matrix}$

переписать как:

$\begin{matrix} \frac{d ω}{d t} = - J^{- 1} F ω + J^{- 1} T \\ y = ω . \end{matrix}$

Тогда матрицы пространства состояний:

$A = - J^{- 1} F, B = J^{- 1}, C = I, D = 0.$

Чтобы создать эту модель, введите следующие команды:

J = [8 -3 -3; -3 8 -3; -3 -3 8];
F = 0.2*eye(3);
A = -J\F;
B = inv(J);
C = eye(3);
D = 0;
sys_mimo = ss(A,B,C,D);

Эти команды предполагают, что J является тензором инерции куба, вращающегося вокруг его угла, и демпфирующая сила имеет величину 0,2.

sys_mimo является ss модель.

Модели пространства состояний дескриптора MIMO

В этом примере показано, как создать модель пространства дескрипторов (неявных) в непрерывном времени с использованием dss.

Этот пример использует ту же систему вращающегося тела, показанную в MIMO Explicit State-Space Models, где вы инвертировали матрицу инерции J, чтобы получить значение матрицы B. Если J плохо обусловлена для инверсии, можно вместо этого использовать дескрипторную (неявную) модель пространства состояний. A descriptor (implicit) state-space model имеет форму:

$\begin{matrix} E \frac{d x}{d t} = A x + B u \\ y = C x + D u \end{matrix}$

Создайте модель пространства состояний для вращающегося тела с J тензора инерции, F демпфирующей силы и тремя осями вращения, связанными с:

$\begin{matrix} J \frac{d ω}{d t} + F ω = T \\ y = ω . \end{matrix}$

Входной T системы является приводным крутящим моментом. Выходной y является вектором скоростей вращения вращающегося тела. Можно записать эту систему как модель пространства состояний дескриптора, имеющую следующие матрицы пространства состояний:

$A = - F, B = I, C = I, D = 0, E = J .$

Для создания этой системы введите:

J = [8 -3 -3; -3 8 -3; -3 -3 8];
F = 0.2*eye(3);
A = -F;
B = eye(3);
C = eye(3);
D = 0;
E = J;
sys_mimo = dss(A,B,C,D,E)

sys является ss модель с непустой матрицей E.

Космическая модель реактивного транспортного самолета

В этом примере показано, как создать модель MIMO реактивного транспорта. Поскольку разработка физической модели для реактивного самолета является длительной, здесь представлены только уравнения пространства состояний. Смотрите любой стандартный текст в авиации для более полного обсуждения физики за рейсом самолета.

Реактивная модель во время круизного рейса на MACH = 0,8 и H = 40000 футов.

A = [-0.0558   -0.9968    0.0802    0.0415
      0.5980   -0.1150   -0.0318         0
     -3.0500    0.3880   -0.4650         0
           0    0.0805    1.0000         0];

B = [ 0.0073         0
     -0.4750    0.0077
      0.1530    0.1430
           0         0];

C = [0     1     0     0
     0     0     0     1];

D = [0     0
     0     0];

Используйте следующие команды, чтобы задать эту модель пространства состояний как объект LTI и прикрепить имена к состояниям, входам и выходам.

states = {'beta' 'yaw' 'roll' 'phi'};
inputs = {'rudder' 'aileron'};
outputs = {'yaw rate' 'bank angle'};

sys_mimo = ss(A,B,C,D,'statename',states,...
'inputname',inputs,...
'outputname',outputs);

Можно отобразить модель LTI, набрав sys_mimo.

sys_mimo

 
a = 
                      beta          yaw         roll          phi
         beta      -0.0558      -0.9968       0.0802       0.0415
          yaw        0.598       -0.115      -0.0318            0
         roll        -3.05        0.388       -0.465            0
          phi            0       0.0805            1            0
 
 
b = 
                    rudder      aileron
         beta       0.0073            0
          yaw       -0.475       0.0077
         roll        0.153        0.143
          phi            0            0
 
 
c = 
                      beta          yaw         roll          phi
     yaw rate            0            1            0            0
   bank angle            0            0            0            1
 
 
d = 
                    rudder      aileron
     yaw rate            0            0
   bank angle            0            0
 
Continuous-time model.

Модель имеет два входа и два выхода. Модулями являются радианы для beta (угол боковой кромки) и phi (угол банка) и радианы/с для yaw (скорость рыскания) и roll (скорость крена). Отклонения руля и элерона указаны в степенях.

Как и в случае SISO, используйте tf для вывода представления передаточной функции.

tf(sys_mimo)

 
Transfer function from input "rudder" to output...
               -0.475 s^3 - 0.2479 s^2 - 0.1187 s - 0.05633
 yaw rate:  ---------------------------------------------------
            s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674
 
                         0.1148 s^2 - 0.2004 s - 1.373
 bank angle:  ---------------------------------------------------
              s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674
 
Transfer function from input "aileron" to output...
            0.0077 s^3 - 0.0005372 s^2 + 0.008688 s + 0.004523
 yaw rate:  ---------------------------------------------------
            s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674
 
                        0.1436 s^2 + 0.02737 s + 0.1104
 bank angle:  ---------------------------------------------------
              s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674

См. также

ss

Документация