Документация

Что такое сплайн Чебышева?

Сплайн Чебышева <reservedrangesplaceholder30>=<reservedrangesplaceholder29><reservedrangesplaceholder28>=<reservedrangesplaceholder27><reservedrangesplaceholder26>_, t _{порядка <reservedrangesplaceholder24>} для последовательности узла t = (t i: <reservedrangesplaceholder20> =1: n + k), уникальный элемент <reservedrangesplaceholder17> <reservedrangesplaceholder16>, t макс. нормы 1, который максимально колеблется на интервале [<reservedrangesplaceholder14> <reservedrangesplaceholder13>. <reservedrangesplaceholder12> <reservedrangesplaceholder11> +1] и является положительным близким <reservedrangesplaceholder10> <reservedrangesplaceholder9> +1. Это означает, что есть уникальное строго увеличение n - последовательность τ так, чтобы функция <reservedrangesplaceholder7>=<reservedrangesplaceholder6><reservedrangesplaceholder5>∊<reservedrangesplaceholder4><reservedrangesplaceholder3>, t данный C (τ <reservedrangesplaceholder0>) = (-1)^{n – 1}, весь i, имеет макс. норму 1 на [<reservedrangesplaceholder23> <reservedrangesplaceholder22>_{. <reservedrangesplaceholder21> <reservedrangesplaceholder20> +1}]. Это подразумевает, что .r1 = t k, .r n = t n + 1, и что t i < .ri < t k + i, для всех i. На самом деле t i+1 ≤ .ri ≤ t i + k _-1, все i. Это поднимает точку, что последовательность узлов принята, чтобы сделать такое неравенство возможным, т.е. элементы S k, t приняты непрерывными.

Короче говоря, сплайн Чебышёва C выглядит так же, как полином Чебышева. Он выполняет аналогичные функции. Для примера, его крайние сайты и особенно хорошие сайты для интерполяции с S _k, t потому что норма получившегося проектора примерно такая маленькая, как может быть; см. команду тулбоксаchbpnt.

Можно запустить пример Конструкция сплайна Чебышева, чтобы создать C для определенного t последовательности узлов.

Выбор Сплайна Пространства

Вы имеете дело с кубическими сплайнами, то есть с порядком

k = 4;

и используйте последовательность пропуска

breaks = [0 1 1.1 3 5 5.5 7 7.1 7.2 8];
lp1 = length(breaks); 

и использовать простые внутренние узлы, т.е. использовать последовательность узлов

t = breaks([ones(1,k) 2:(lp1-1) lp1(:,ones(1,k))]);
n = length(t)-k;

Обратите внимание на четверной узел на каждом конце. Потому что k = 4, это делает [0.. 8] = [breaks(1). breaks(lp1)] интересующий интервал [t k.. _t n + 1] с n = length(t)- kРазмерность полученного сплайна пространства S _k, t. Та же последовательность узлов была бы обеспечена

t=augknt(breaks,k);

Начальное предположение

Как начальное предположение для, используйте средние значения

рекомендуемый как хороший выбор сайта интерполяции. Они поставляются

tau=aveknt(t,k); 

Постройте график полученного первого приближения, чтобы C, т.е. сплайн c, который удовлетворяет c (^n-–i, все i:

b = cumprod(repmat(-1,1,n)); b = b*b(end);
c = spapi(t,tau,b); 
fnplt(c,'-.') 
grid

Вот получившийся график.

Итерация Ремеза

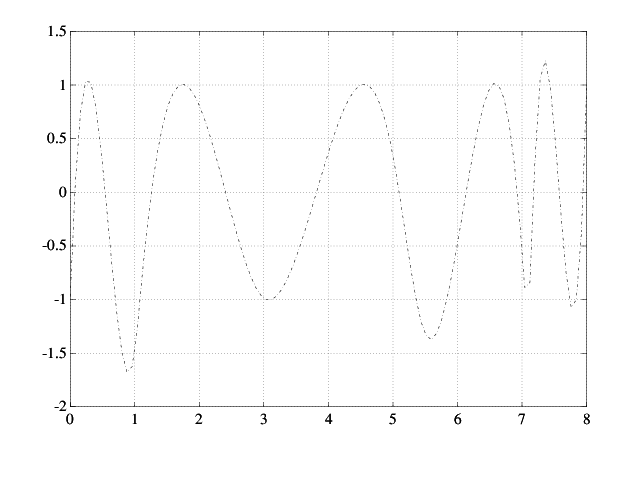
Начиная с этого приближения, вы используете алгоритм Ремеза, чтобы создать последовательность сплайнов, сходящихся к C. Это означает, что вы создадите новый, как экстремум вашего текущего приближения c чтобы C и попробовать еще раз. Вот весь цикл.

Вы находите новый интерьер _в виде нулей Dc, то есть первую производную c, в несколько шагов. Во-первых, дифференцируйте:

Dc = fnder(c);

Далее примите нули управляющего многоугольника Dc как первое предположение для нулей Dc. Для этого необходимо разобрать сплайн Dc.

[knots,coefs,np,kp] = fnbrk(Dc,'knots','coefs','n','order');

Управляющий многоугольник имеет вершины (tstar(i), coefs(i)), с tstar средние средние значения узла для сплайна, обеспечиваемое aveknt:

tstar = aveknt(knots,kp);

Вот нули получившегося многоугольника Dc:

npp = (1:np-1); 
guess = tstar(npp) -coefs(npp).*(diff(tstar)./diff(coefs));

Это уже дает очень хорошее первое предположение по фактическим нулям.

Уточните эту оценку для нулей Dc на два шага секантного метода, принимая tau и результирующие guess как ваши первые приближения. Во-первых, оцените Dc на обоих наборах:

sites = tau(ones(4,1),2:n-1); 
sites(1,:) = guess; 
values = zeros(4,n-2); 
values(1:2,:) = reshape(fnval(Dc,sites(1:2,:)),2,n-2);

Теперь придут два шага секантного метода. Вы защищаете от деления на ноль путем установки различия значений функции равной 1 в случае, если она равна нулю. Поскольку Dc строго монотонна рядом с искомыми сайтами, это безвредно:

for j=2:3 
  rows = [j,j-1];Dcd=diff(values(rows,:));
  Dcd(find(Dcd==0)) = 1; 
  sites(j+1,:) = sites(j,:) ... 
           -values(j,:).*(diff(sites(rows,:))./Dcd); 
  values(j+1,:) = fnval(Dc,sites(j+1,:)); 
end

Проверка

max(abs(values.')) 
  ans = 4.1176 5.7789 0.4644 0.1178

показывает улучшение.

Теперь примите эти сайты как свои новые tau,

tau = [tau(1) sites(4,:) tau(n)];

и проверяйте значения экстремумов вашего текущего приближения там:

extremes = abs(fnval(c, tau));

Различие

max(extremes)-min(extremes)
  ans = 0.6905

является оценкой того, как далеко вы находитесь от общего выравнивания.

Создайте новый сплайн, соответствующий новому выбору tau и постройте его поверх старого:

c = spapi(t,tau,b); 
sites = sort([tau (0:100)*(t(n+1)-t(k))/100]); 
values = fnval(c,sites); 
hold on, plot(sites,values)

Следующий код включает сетку и строит графики местоположений extrema.

grid on
plot( tau(2:end-1), zeros( 1, np-1 ), 'o' )
hold off
legend( 'Initial Guess', 'Current Guess', 'Extreme Locations',...
 'location', 'NorthEastOutside' );

Ниже приводится получившийся рисунок (легенда не показана).

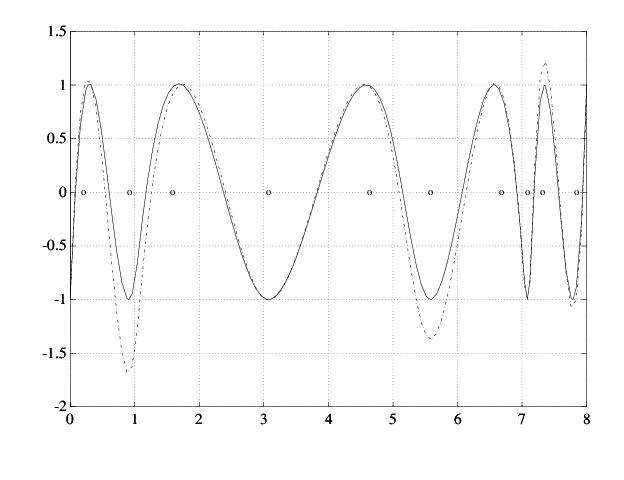
Если это недостаточно близко, цикл просто повторяется. В данном примере следующая итерация уже создает C к графической точности.