Настраиваемый линейный подбор кривой

Сведения о пользовательских линейных моделях

В приложении Аппроксимирование Кривыми можно использовать Custom Equation подходит для определения собственных линейных или нелинейных уравнений. Пользовательская подгонка уравнения использует процедуру нелинейного метода наименьших квадратов аппроксимации.

Вы можете задать пользовательское линейное уравнение в Custom Equation, но нелинейный подбор кривой менее эффективна и обычно медленнее, чем линейный метод наименьших квадратов подбора кривой. Если вам нужна линейный метод наименьших квадратов подгонка для пользовательских уравнений, выберите Linear Fitting вместо этого. Линейные модели являются линейными комбинациями (возможно, нелинейных) членов. Они заданы уравнениями, которые являются линейными в параметрах.

Совет

Если вам нужна линейный метод наименьших квадратов подгонка для пользовательских уравнений, выберите Linear Fitting. Если вы не знаете, может ли ваше уравнение быть выражено как набор линейных функций, выберите Custom Equation вместо этого. Смотрите Выбор Пользовательского Уравнения Подгонки Интерактивно.

Интерактивный выбор пользовательской подгонки линейного фитинга

В приложении Аппроксимирование Кривыми выберите некоторые данные кривой в списках X data и Y data. Вы можете видеть только Linear Fitting в списке типов модели после выбора некоторых данных кривых, поскольку Linear Fitting для кривых, а не поверхностей.
Аппроксимирование кривыми приложение создает аппроксимация полиномом по умолчанию.
Измените тип модели из Polynomial на Linear Fitting в списке типов модели.
Пример уравнения появляется, когда вы выбираете Linear Fitting из списка.
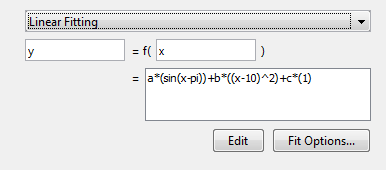
Можно изменить x и y ко всем допустимым именам переменной.
В нижнем поле отображается пример уравнения. Щелкните Edit, чтобы изменить условия примера в диалоговом окне Edit Custom Linear Terms и определить собственное уравнение.

Для получения примера смотрите Подгонку Custom Linear Legendre Полиномов в Аппроксимирование кривыми Приложения.

Выбор линейного подбора кривой в командной строке

Чтобы использовать линейный алгоритм аппроксимации, задайте массив ячеек из членов модели как вход в fit или fittype функций. Не включать коэффициенты в выражения терминов. Если существует постоянный термин, используйте '1' в качестве соответствующего выражения в массиве ячеек.

Чтобы задать линейную модель следующей формы:

 coeff1 * term1 + coeff2 * term2 + coeff3 * term3 + ...

где ни один коэффициент не появляется ни в одном из term1, term2, и т.д., используйте массив ячеек, где каждый член, без коэффициентов, задан в массиве ячеек строк следующим образом:

LinearModelTerms = {'term1', 'term2', 'term3', ... }

Идентифицируйте линейные условия модели, в которые вы должны ввести fittype. Для примера, модель
```
a*log(x) + b*x + c
```
линейный в a, b, и c. У него три условия log(x), x, и 1 (потому что c=c*1). Чтобы задать эту модель, вы используете этот массив ячеек терминов: LinearModelTerms = {'log(x)','x','1'}.
Используйте массив ячеек линейных членов модели в качестве входов для fittype функция:
```
linearfittype = fittype({'log(x)','x','1'})
```
```
linearfittype = 

     Linear model:
     linearfittype(a,b,c,x) = a*log(x) + b*x + c
```

Загрузите некоторые данные и используйте fittype как вход в fit функция.

load census
f = fit(cdate,pop,linearfittype)

f = 

     Linear model:
     f(x) = a*log(x) + b*x + c
     Coefficients (with 95% confidence bounds):
       a =  -4.663e+04  (-4.973e+04, -4.352e+04)
       b =        25.9  (24.26, 27.55)
       c =   3.029e+05  (2.826e+05, 3.232e+05)

Кроме того, можно задать массив ячеек линейных модельных членов как вход в fit функция:

f = fit(x,z,{'log(x)','x','1'})

Постройте график подгонки и данных.
```
plot(f,cdate,pop)
```

Для получения примера смотрите Подгонку Полиномов Custom Linear Legendre в командной строке.

Подгонка пользовательских линейных полиномов легенды

Подгонка пользовательских линейных полиномов Legendre в приложение Аппроксимирование Кривыми

Этот пример показывает аппроксимацию данных с помощью нескольких пользовательских линейных уравнений. Данные сгенерированы и основаны на ядерной реакции ¹²C (e, e 'α)⁸Будь. В уравнениях используются суммы полиномиальных членов Legendre.

Рассмотрим эксперимент, в котором 124 МэнВ-электрона рассеиваются из ¹²Ядра C. В последующей реакции альфа-частицы испускаются и образуют остаточные ядра ⁸Будь. Анализируя количество альфа-частиц, испускаемых как функция угла, можно вывести определенную информацию, касающуюся ядерной динамики ¹²Далее показана кинематика реакции.

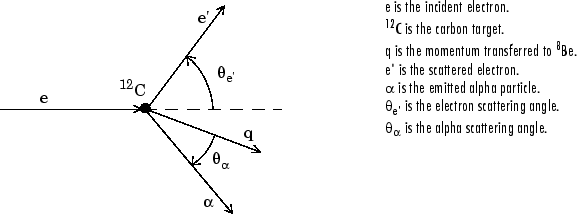
Данные собирают путем размещения твердых детекторов состояния на значениях^o к 240^o в 10^o шаги.

Иногда полезно описать переменную, выраженную в функции угла в терминах полиномов Лежандра

$y (x) = \sum_{n = 0}^{\infty} a_{n} P_{n} (x)$

где _Pn (x) является полиномом Лежандра степени n, x есть cos ₍в α), и an являются коэффициентами подгонки. Для получения информации о генерации полиномов Legendre, см. legendre функция.

Для данных альфа-эмиссии можно непосредственно связать коэффициенты с ядерной динамикой, активировав теоретическую модель. Кроме того, теоретическая модель вводит ограничения для бесконечной суммы, показанной выше. В частности, рассматривая угловой импульс реакции, полином Лежандра четвертой степени, использующий только четные условия, должен эффективно описывать данные.

Можно сгенерировать полиномы Лежандра с формулой Родригеса:

$P_{n} (x) = \frac{1}{2^{n} n!} {(\frac{d}{d x})}^{n} {(x^{2} - 1)}^{n}$

Легендарные полиномы до четвертой степени

n	_Pn (x)
0	1
1	x
2	(1/2) (3 x²– 1)
3	(1/2) (5 x³ – 3 x)
4	(1/8) (35 x⁴ – 30 x² + 3)

Этот пример показывает аппроксимацию данных с помощью полинома Legendre четвертой степени только с четными терминами:

$y_{1} (x) = a_{0} + a_{2} (\frac{1}{2}) (3 x^{2} - 1) + a_{4} (\frac{1}{8}) (35 x^{4} - 30 x^{2} + 3)$

Загрузите ¹²Данные о альфа-выбросах C путем ввода
```
load carbon12alpha
```
Теперь рабочая область содержит две новые переменные:
- angle - вектор углов (в радианах) в диапазоне от 10^o к 240^o в 10^o шаги.
- counts - вектор подсчётов необработанных альфа-частиц, которые соответствуют углам излучения в angle.
Откройте приложение Аппроксимирование Кривыми, введя:
```
cftool
```
В приложении Аппроксимирование Кривыми выберите angle и counts для X data и Y data, чтобы создать аппроксимацию полиномом по умолчанию для двух переменных.
Измените тип модели на Polynomial на Linear Fitting для создания пользовательской линейной подгонки по умолчанию.
Вы используете Linear Fitting вместо Custom Equation подгонка типа, потому что полиномы Лежандра зависят только от переменной предиктора и констант. Уравнение, которое вы зададите для модели, является y 1 (x) (то есть уравнение, данное в начале этой процедуры). Потому что angle дается в радианах, аргумент терминов Legendre задается cos (
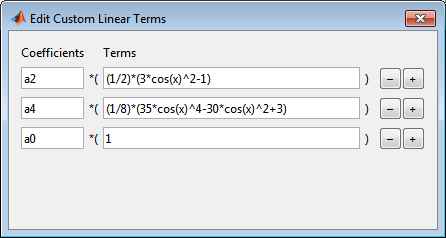
Щелкните Edit, чтобы изменить условия уравнения в диалоговом окне «Редактирование пользовательских линейных терминов».
1. Измените имена Coefficients на a2, a4, и a0.
2. Измените Terms на a2 кому
```
(1/2)*(3*cos(x)^2-1)
```
  Приложение Аппроксимирование Кривыми обновляет подгонку при редактировании условий.
3. Измените Terms на a4 кому
```
(1/8)*(35*cos(x)^4-30*cos(x)^2+3)
```
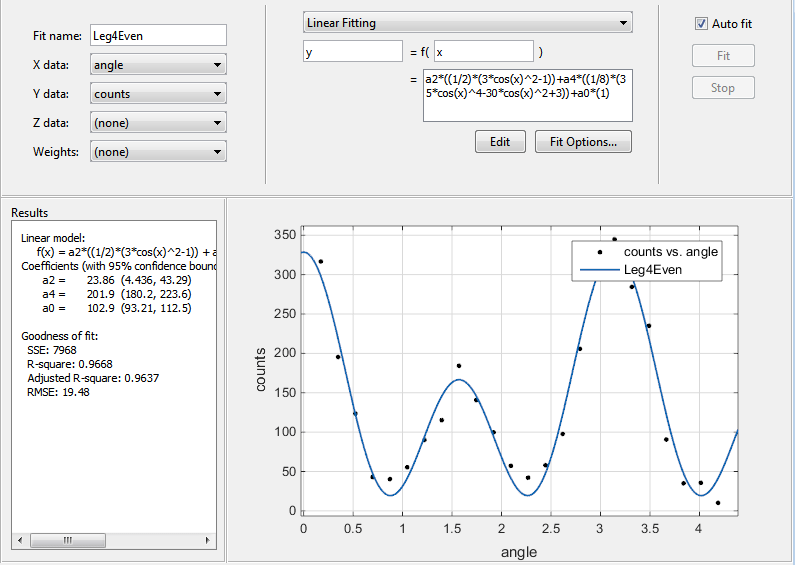
  Подгонка появляется в приложении Аппроксимирование Кривыми.

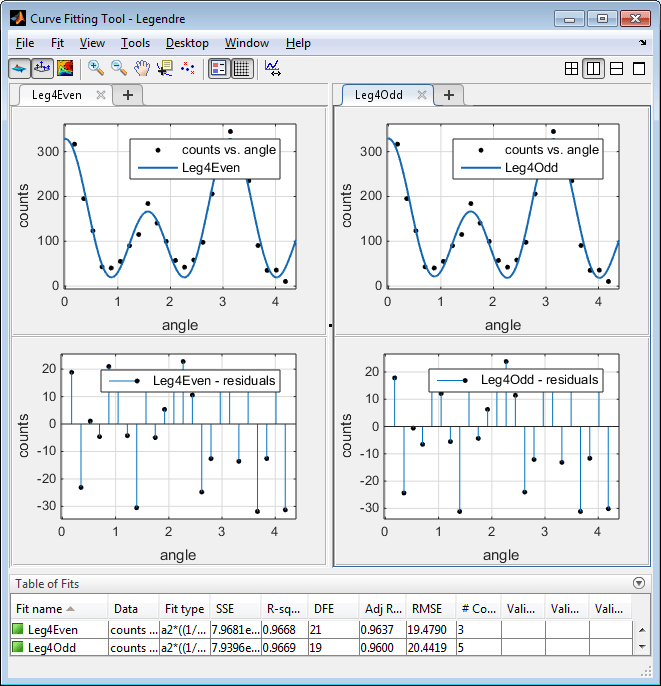
Переименуйте Fit name в Leg4Even.
Отобразить невязки можно путем выбора View > Residuals Plot.
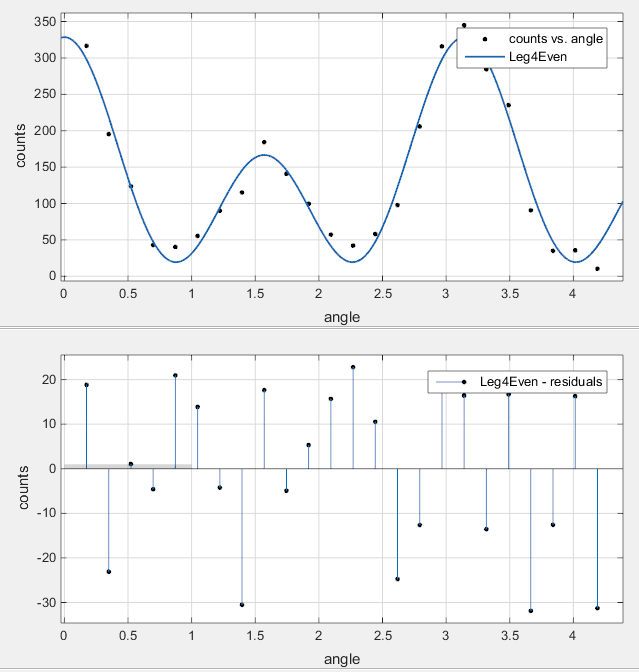
Подгонка, по-видимому, хорошо соответствует тренду данных, в то время как невязки, по-видимому, распределены случайным образом и не показывают какого-либо систематического поведения.
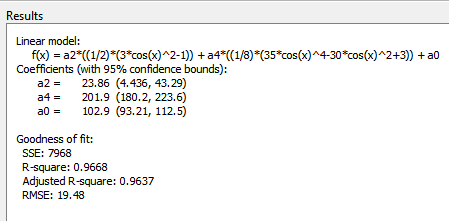
Исследуйте результаты численного подгонки на панели Results. Посмотрите на каждое значение коэффициента и его доверительные границы в круглых скобках. 95% доверительных границ указывают, что коэффициенты, сопоставленные с a 0 (x) и a 4 (x), известны довольно точно, но что коэффициент a 2 (x) имеет относительно большую неопределенность.
Выберите Fit > Duplicate Leg4Even, чтобы создать копию предыдущей аппроксимации полиномом Legendre для изменения.
Дублированная подгонка появится на новой вкладке.
Чтобы подтвердить теоретический аргумент о том, что данные альфа-эмиссии лучше всего описаны полиномом Легендра четвертой степени с только четными терминами, затем подбирайте данные с помощью как четных, так и нечетных членов:
$y_{2} (x) = y_{1} (x) + a_{1} x + a_{3} (\frac{1}{2}) (5 x^{3} - 3 x)$
Переименуйте новую подгонку в Leg4EvenOdd.
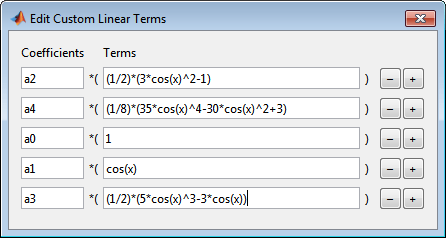
Щелкните Edit, чтобы изменить условия уравнения. Откроется диалоговое окно Править пользовательские линейные условия (Edit Custom Linear Terms).
Измените условия следующим образом, чтобы соответствовать модели, заданной y 2 (x):
1. Нажмите кнопку +, чтобы добавить термин дважды, чтобы добавить нечетные условия Legendre.
2. Измените имена новых коэффициентов на a1 и a3.
3. Измените Terms на a1 кому
```
cos(x)
```
4. Измените Terms на a3 кому
```
pro(1/2)*(5*cos(x)^3-3*cos(x))
```
Наблюдайте новую подгонку, нанесенную в приложении Аппроксимирование Кривыми, и исследуйте числовые результаты на панели Results.
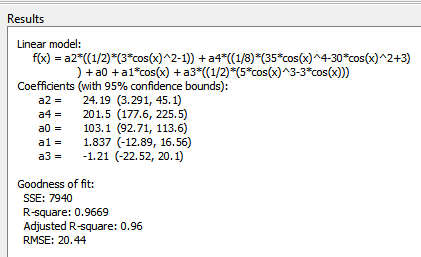
Обратите внимание, что нечетные коэффициенты Лежандра (a1 и a3) являются вероятными кандидатами для удаления, чтобы упростить подгонку, потому что их значения малы, а доверительные границы содержат нуль. Эти результаты указывают, что нечетные условия Legendre не вносят существенного вклада в подгонку, а четные условия Legendre по сути не изменяются по сравнению с предыдущей подгонкой. Это подтверждает, что начальный выбор модели в Leg4Even подгонка - лучший.
Чтобы сравнить модели один за другим, выберите Left/Right плитку. Отображать можно только графики, скрывая настройки подгонки и панели результатов с помощью меню View приложения Аппроксимирование Кривыми.

Подбор пользовательских линейных полиномов легенды в командной строке

Подгонка той же модели в командной строке, которую вы создали в приложении Аппроксимирование Кривыми.

Чтобы использовать линейный алгоритм аппроксимации, задайте массив ячеек из членов модели как вход в fittype функция. Используйте то же Terms, что вы ввели в приложении Аппроксимирование Кривыми для Leg4Even подгонка, и не задавать никаких коэффициентов.
```
linearft = fittype({'(1/2)*(3*cos(x)^2-1)', ...
'(1/8)*(35*cos(x)^4-30*cos(x)^2+3)','1'})
```
```
linearft = 

     Linear model:
     linearft(a,b,c,x) = a*((1/2)*(3*cos(x)^2-1))...
       + b*((1/8)*(35*cos(x)^4-30*cos(x)^2+3)) + c
```
Загрузите angle и counts переменные в рабочей области.
```
load carbon12alpha
```

Используйте fittype как вход в fit function, и задать angle и counts переменные в рабочей области.

f = fit(angle, counts, linearft)

f = 

     Linear model:
     f(x) = a*((1/2)*(3*cos(x)^2-1))...
     + b*((1/8)*(35*cos(x)^4-30*cos(x)^2+3)) + c
     Coefficients (with 95% confidence bounds):
       a =       23.86  (4.436, 43.29)
       b =       201.9  (180.2, 223.6)
       c =       102.9  (93.21, 112.5)

Постройте график подгонки и данных.
```
plot(f, angle, counts)
```

Для получения дополнительной информации о терминах линейной модели см. fittype функция.

Документация