Интерполяция является процессом для оценки значений, которые находятся между известными точками данных.
Интерполяция включает конструкцию функции f , которая совпадает с заданными значениями данных, yi, на заданных сайтах данных, xi, в том смысле, что f (xi) = yi, все i.
Интерполяция, f, обычно строится как уникальная функция вида
который соответствует заданным данным с функциями, которые fj выбраны «соответствующим образом».
В интерполяции сплайна каждый выбирает fj, чтобы быть n последовательными B-сплайнами Bj (<reservedrangesplaceholder14>) = B (x | tj..., <reservedrangesplaceholder10> <reservedrangesplaceholder9> + k), j = 1: n, порядка <reservedrangesplaceholder5> для некоторой последовательности <reservedrangesplaceholder4> 1 <reservedrangesplaceholder3> 2 узла... <reservedrangesplaceholder2> <reservedrangesplaceholder1> + k.
Метод | Описание |
|---|---|
Линейный | Линейная интерполяция. Этот метод подходит для другого линейного полинома между каждой парой точек данных для кривых или между наборами трех точек для поверхностей. |
Ближайшая соседка | Интерполяция по ближайшему соседу. Этот метод устанавливает значение интерполированной точки на значение ближайшей точки данных. Поэтому этот метод не генерирует никаких новых точек данных. |
Кубический сплайн | Кубическая сплайн интерполяция. Этот метод подходит для другого кубического полинома между каждой парой точек данных для кривых или между наборами трех точек для поверхностей. |
Сохранение формы | Кусочно-кубическая эрмитовая интерполяция (PCHIP). Этот метод сохраняет монотонность и форму данных. Только для кривых. |
Бихармония (v4) | MATLAB® 4 Только для поверхностей. |
Тонкопластинчатый сплайн | Тонкопластинчатая сплайн интерполяция. Этот метод подходит для гладких поверхностей, которые также хорошо экстраполируются. Только для поверхностей. |
Для поверхностей в типе Interpolant fit используется MATLAB scatteredInterpolant функция для линейных и ближайших методов и MATLAB griddata функция для кубических и бигармонических методов. Метод тонкопластинчатого сплайна использует tpaps функция.
Тип интерполяции для использования зависит от характеристик подгоняемых данных, необходимой плавности кривой, факторов скорости, требований анализа после подгонки и так далее. Линейные и ближайшие соседние методы быстрые, но получившиеся кривые не очень гладкие. Кубический сплайн и методы сохранения формы и v4 медленнее, но получившиеся кривые очень плавны.
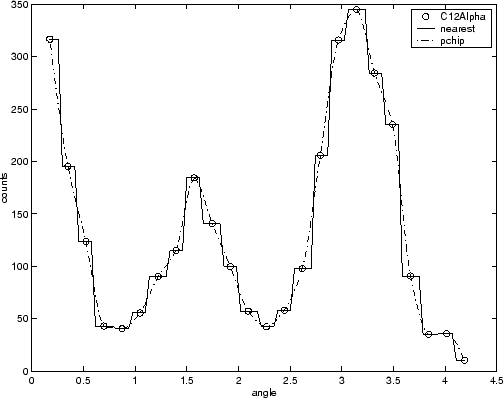
Для примера, данные ядерной реакции от carbon12alpha.mat файл показан здесь с самой близкой соседней интерполяционной подгонкой и с сохраняющей форму (PCHIP) интерполяционной подгонкой. Очевидно, что интерполяция по ближайшему соседу не следует данным, а также сохраняющей форму интерполяции. Различие между этот два подгонке может быть важным, если вы интерполируете. Однако, если вы хотите интегрировать данные, чтобы получить представление о общей силе реакции, то оба подгонка обеспечивают почти одинаковые ответы для разумных ширин интервала интегрирования.
Примечание
Статистика качества подгонки, границы предсказания и веса не определены для интерполяций. Кроме того, невязки подгонки всегда равны 0 (в пределах компьютерной точности), потому что интерполяции прохода через данные точки.
Интерполяции определяются как кусочные полиномы, потому что подобранная кривая построена из многих «частей» (кроме Biharmonic для поверхностей, который является интерполяцией радиального базиса функций). Для кубического сплайна и PCHIP интерполяции каждая часть описывается четырьмя коэффициентами, которые тулбокс вычисляет с помощью кубического (третьей степени) полинома.
См. spline для получения дополнительной информации о кубической сплайн интерполяции.
См. pchip функция для получения дополнительной информации о сохраняющей форму интерполяции и для сравнения двух методов.
Обратитесь к scatteredInterpolant, griddata, и tpaps функции для получения дополнительной информации о поверхностной интерполяции.
Возможно аппроксимировать одну «глобальную» полиномиальную интерполяцию к данным со степенью на единицу меньше, чем количество точек данных. Однако такая подгонка может иметь дико неустойчивое поведение между точками данных. Напротив, кусочные полиномы, описанные здесь, всегда создают хорошо себя подгонку, поэтому они более гибки, чем параметрические полиномы, и могут эффективно использоваться для более широкой области значений наборов данных.