Тулбокс обеспечивает (полиномиальные) функции сплайна в любом количестве переменных, как тензорные продукты одномерных сплайнов. Эти многомерные сплайны имеют обе стандартные формы, B-форму и ppform, а их конструкция и использование параллелей полностью аналогичны одномерным сплайнам, рассмотренным в предыдущих разделах, Строительство и Работа со сплайнами и Построение и Работа со сплайнами B-формы. Те же команды используются для их конструкции и использования.
Для простоты в следующем обсуждении рассматриваются просто двухмерные сплайны.
Идея тензор-продукт очень проста. Если f является функцией x, а g является функцией y, то их тензор-произведение p (x,y): = f (x) g (y) является функцией x и y, т.е. двухмерная функция. В более общем плане, с s = (s 1..., <reservedrangesplaceholder13> <reservedrangesplaceholder12> + h) и t = (t 1..., <reservedrangesplaceholder8> <reservedrangesplaceholder7> + k) связывают узлом последовательности и <reservedrangesplaceholder5> <reservedrangesplaceholder4> (i = 1..., m; j = 1,... n) соответствующий массив коэффициентов, вы получаете двухмерный сплайн как
B-форма этого сплайна содержит массив ячеек {s, t} его последовательностей узлов, a массива коэффициентов, вектор чисел [m, n] и вектор порядков [h, k]. Команда
sp = spmak({s,t},a);
создает эту форму. Далее, fnplt, fnval, fnder, fndir, fnrfn, и fn2fm может использоваться для построения, вычисления, дифференцирования и интегрирования, уточнения и преобразования этой формы.
Вы, скорее всего, создадите такую форму, ища интерполяцию или аппроксимацию к данным с сеткой. Например, если Вы знаете значения z (i, j) =g (x (<reservedrangesplaceholder8>), y (<reservedrangesplaceholder6>)), <reservedrangesplaceholder5> =1: m, <reservedrangesplaceholder3> =1: n, некоторой функции g во всех точках в прямоугольной сетке, тогда, предполагая, что строго увеличивающаяся последовательность xудовлетворяет условиям Шёнберга-Уитни относительно вышеуказанных s последовательности узлов и что строго увеличивающаяся последовательность y удовлетворяет условиям Шёнберга-Уитни относительно вышеописанных t последовательности узлов, команды
sp=spapi({s,t},[h,k],{x,y},z);создает уникальный двухмерный сплайн вышеописанной формы, который соответствует заданным значениям. Область команды fnplt(sp) дает вам быстрый график этой интерполяции. Область команды pp = fn2fm(sp,'pp') предоставляет вам форму ppform этого сплайна, которая, вероятно, является тем, что вы хотите, когда хотите вычислить сплайн в тонкой сетке ( (xx(i),yy(j))для i=1:M, j=1:N), по команде:
values = fnval(pp,{xx,yy});
ppform такого двухмерного сплайна содержит, аналогично, массив ячеек из последовательностей пропуска, многомерную матрицу коэффициентов, вектор из чисел и вектор полиномиальных порядков. К счастью, тулбокс настроен таким образом, что для вас обычно нет оснований беспокоиться об этих деталях любой формы. Вы используете интерполяцию, приближение или сглаживание, чтобы создать сплайны, а затем используете fn... команды для их использования.
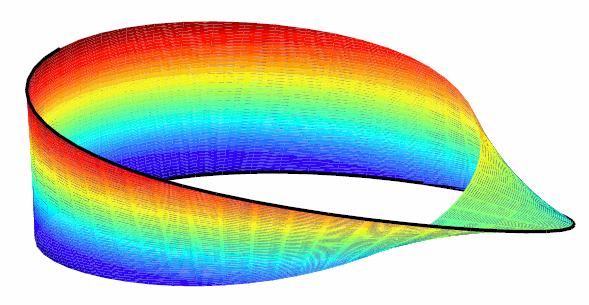
Вот пример поверхности, построенной как 3-D-valued двухмерный сплайн. Поверхность - знаменитая группа Möbius, получаемая путём взятия длинной полосы бумаги и склеивания её узких концов вместе, но с поворотом. Рисунок получается следующими командами:
x = 0:1; y = 0:4; h = 1/4; o2 = 1/sqrt(2); s = 2; ss = 4;
v(3,:,:) = h*[0, -1, -o2, 0, o2, 1, 0;0, 1, o2, 0, -o2, -1, 0];
v(2,:,:) = [ss, 0, s-h*o2, 0, -s-h*o2, 0, ss;...
ss, 0, s+h*o2, 0,-s+h*o2, 0, ss];
v(1,:,:) = s*[0, 1, 0, -1+h, 0, 1, 0; 0, 1, 0, -1-h, 0, 1, 0];
cs = csape({x,y},v,{'variational','clamped'});
fnplt(cs), axis([-2 2 -2.5 2.5 -.5 .5]), shading interp
axis off, hold on
values = squeeze(fnval(cs,{1,linspace(y(1),y(end),51)}));
plot3(values(1,:), values(2,:), values(3,:),'k','linew',2)
view(-149,28), hold off
Möbius Band Made by Vector-Valued бивариатная сплайн интерполяция