Соберите рациональный сплайн
rp = rpmak(breaks,coefs)
rp = rpmak(breaks,coefs,d)
rpmak(breaks,coefs,sizec)
rs = rsmak(knots,coefs)
rs
= rsmak(shape,parameters)
Оба rpmak и rsmak собрать рациональный сплайн из минимальной информации. rsmak также оборудован для обеспечения рациональных сплайнов, которые описывают стандартные геометрические формы. Рациональный сплайн должен быть скалярным или векторным.
rp = rpmak(breaks,coefs) имеет тот же эффект, что и команда ppmak(breaks, coefs) за исключением того, что результат ppform помечен как рациональный сплайн, то есть как rpform.
Чтобы описать, что это означает, позвольте R быть кусочно-полиномиальным, скомпонованным командой ppmak(breaks,coefs), и пусть r (x) = s (x )/ w (x) будет рациональным сплайном, собранным командой rpmak(breaks,coefs). Если v - значение R в x, затем v(1:end-1)/v(end) - значение r в x. Другими словами, R (x) = [s (x); w (x)]. Соответственно, размерность цели r на единицу меньше размерности цели R. В частности, размерность (цели) R должна быть не менее 2, то есть коэффициенты, заданные coefs должен быть d-векторы с d > 1. Посмотрите ppmak для того, как вход arrays breaks и coefs интерпретируются, следовательно, как они должны быть определены в порядок для получения конкретного кусочного полинома.
rp = rpmak(breaks,coefs,d) имеет тот же эффект, что и ppmak(breaks,coefs,d+1), за исключением того, что полученный ppform помечен как rpform. Обратите внимание, что желание иметь этот необязательный третий аргумент, задающий размерность целевого объекта, требует для него различных значений в rpmak и ppmak для того же массива коэффициентов coefs.
rpmak(breaks,coefs,sizec) имеет тот же эффект, что и ppmak(breaks,coefs,sizec) кроме того, что полученный ppform помечен как rpform, и целевая размерность принято за sizec(1)-1.
rs = rsmak(knots,coefs) аналогично связан с spmak(knots,coefs), и rsmak(knots,coefs,sizec) на spmak(knots,coefs,sizec). В частности, rsmak(knots,coefs) помещает рациональный сплайн в B-форму, т.е. обеспечивает rBform. Посмотрите spmak для того, как вход arrays knots и coefs интерпретируются, следовательно, как они должны быть определены в порядок для получения конкретного кусочного полинома.
rs
= rsmak(shape,parameters) обеспечивает рациональный сплайн в rBform, который описывает форму, заданный вектор символов shape и дополнительные дополнительные parameters. Конкретными вариантами являются:
rsmak('arc',radius,center,[alpha,beta])
rsmak('circle',radius,center)
rsmak('cone',radius,halfheight)
rsmak('cylinder',radius,height)
rsmak('southcap',radius,center)
rsmak('torus',radius,ratio)
с 1 значение по умолчанию для radius, halfheight и height, и источник по умолчанию для centerи дуга, проходящая через все углы от alpha на beta (по умолчанию является [-pi/2,pi/2]), и конус, цилиндр и тор с центром в источник с их основной окружностью в (x, y) -плане, и малая окружность тора с радиусом radius*ratio, по умолчанию для ratio будучи 1/3.
Из них можно сгенерировать родственные формы путем аффинных преобразований с помощью fncmb(rs,transformation).
Все fn... команды кроме fnint, fnder, fndir может обрабатывать рациональные сплайны.
Команды
runges = rsmak([-5 -5 -5 5 5 5],[1 1 1; 26 -24 26]); rungep = rpmak([-5 5],[0 0 1; 1 -10 26],1);
оба обеспечивают описание рационального полинома r (x) = 1/( x2 + 1) на интервале [-5.. 5]. Однако вне интервала [-5.. 5], функция, заданная runges равен нулю, в то время как рациональный сплайн, заданный rungep соглашается с 1/( x2 + 1) на каждую x.
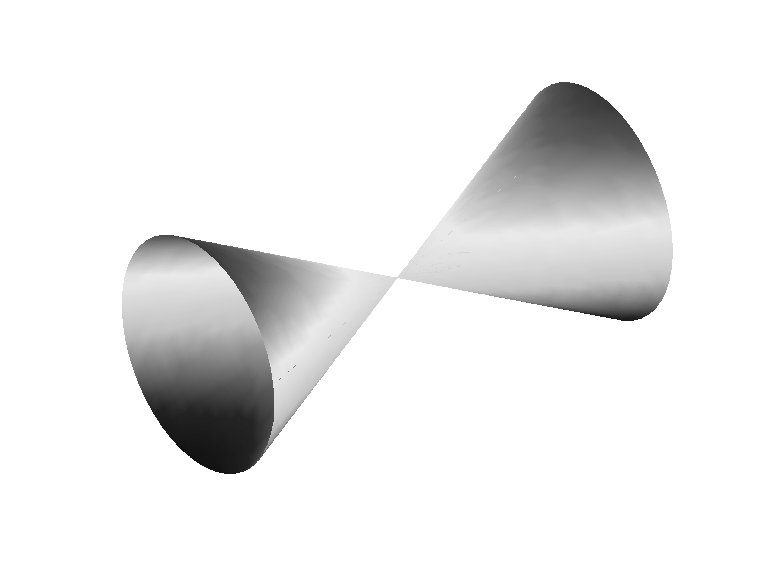
Рисунок повернутого конуса генерируется командами
fnplt(fncmb(rsmak('cone',1,2),[0 0 -1;0 1 0;1 0 0]))
axis equal, axis off, shading interp
Вращенный конус, заданный рациональным квадратичным сплайном
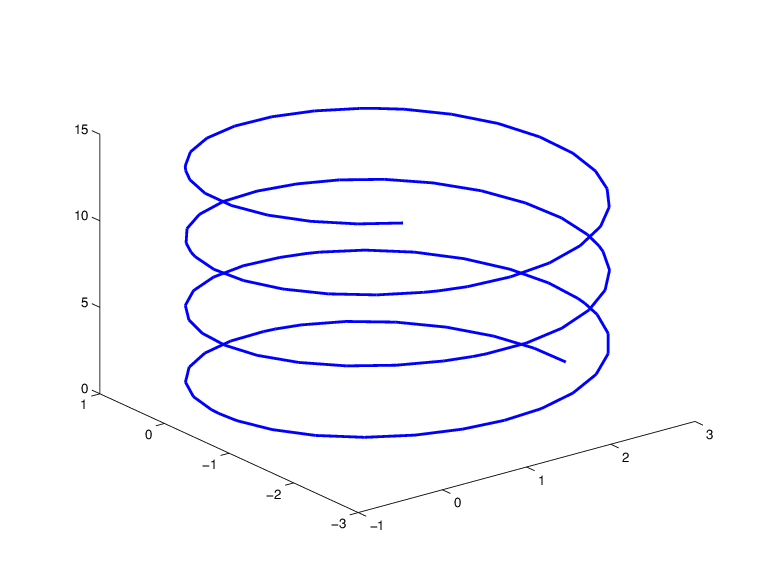
Спираль, показывающая спираль с несколькими обмотками, генерируется командами
arc = rsmak('arc',2,[1;-1],[0 7.3*pi]);
[knots,c] = fnbrk(arc,'k','c');
helix = rsmak(knots, [c(1:2,:);aveknt(knots,3).*c(3,:);
c(3,:)]);
fnplt(helix)
Спираль
Для дополнительных проиллюстрированных примеров см. NURBS и Другие Рациональные Сплайны