Кусочно-двунаправленная эрмитовая интерполяция
c = rscvn(p,u)
c = rscvn(p)
c = rscvn(p,u) возвращает плоскую кусочно-двунаправленную кривую (в квадратичной rBform), которая проходит, по порядку, через заданные точки p(:,j) и строится следующим образом (см. Конструкцию Биарка). Между любыми двумя различными точками p(:,j) и p(:,j+1)кривая обычно состоит из двух круглых дуг (включая прямолинейные сегменты), которые соединяются с непрерывностью тангенса, причем первая дуга начинается с p(:,j) и нормально там, чтобы u(:,j), и вторая дуга, заканчивающаяся на p(:,j+1) и нормально там, чтобы u(:,j+1)и с двумя дугами, написанными как одна, когда это возможно. Таким образом, кривая тангенс-непрерывна везде, кроме, возможно, в повторных точках, где кривая может иметь угол, или когда угол, образованный двумя сегментами, заканчивающимися на p(:,j), является необычно маленьким, в этом случае кривая может иметь cusp в этой точке.
p должна быть действительной матрицей, с двумя строками и по крайней мере двумя столбцами, и любой столбец должен отличаться по крайней мере от одного из соседних столбцов.
u должна быть действительной матрицей с двумя строками, с одинаковым числом столбцов, как p (для двух исключений см. ниже) и не может иметь нулевого столбца.
c = rscvn(p) выбирает нормали следующим образом. Для j=2:end-1, u(:,j) - среднее значение нормали (нормированной, поворотной вправо) к векторам p(:,j)-p(:,j-1) и p(:,j+1)-p(:,j). Если p(:,1)==p(:,end), затем обе конечные нормали выбираются в качестве среднего значения нормалей, которые будут p(:,2)-p(:,1) и p(:,end)-p(:,end-1) таким образом предотвращается угол на получившейся замкнутой кривой. В противном случае конечные нормали выбираются таким образом, чтобы над первым и последним сегментом была только одна дуга (не узловое граничное условие).
rscvn(p,u), с u имея в точности два столбцов, также выбирает внутренние нормали как для случая, когда u отсутствует, но использует два столбца u как нормали конечной точки.
Пример 1. Следующий код генерирует описание круга, используя всего четыре части. За исключением другого масштабирования последовательности узлов, это то же описание, что и предоставлено rsmak('circle',1,[1;1]).
p = [1 0 -1 0 1; 0 1 0 -1 0]; c = rscvn([p(1,:)+1;p(2,:)+1],p);
Тот же круг, но с использованием всего двух частей, обеспечивается
c2 = rscvn([0,2,0; 1,1,1]);
Пример 2. Следующий код изображает две буквы. Обратите внимание, что вторая буква является результатом интерполяции всего до четырех точек. Обратите внимание также на использование перевода в графическом изображении второй буквы.
p = [-1 .8 -1 1 -1 -1 -1; 3 1.75 .5 -1.25 -3 -3 3]; i = eye(2); u = i(:,[2 1 2 1 2 1 1]); B = rscvn(p,u); S = rscvn([1 -1 1 -1; 2.5 2.5 -2.5 -2.5]); fnplt(B), hold on, fnplt(fncmb(S,[3;0])), hold off axis equal, axis off
Две буквы, составленные из круговых дуг

Пример 3. Следующий код генерирует конструкцию биарки, которая используется в обсуждении ниже конструкции биарки, используемой здесь. Обратите внимание на использование fntlr найти тангенс биарки в начале, в точке, где соединяются две дуги, и в конце.
p = [0 1;0 0]; u = [.5 -.1;-.25 .5]; plot(p(1,:),p(2,:),'k'), hold on biarc = rscvn(p,u); breaks = fnbrk(biarc,'b'); fnplt(biarc,breaks(1:2),'b',3), fnplt(biarc,breaks(2:3),'r',3) vd = fntlr(biarc,2,breaks); quiver(vd(1,:),vd(2,:),vd(4,:),-vd(3,:)), hold off
Конструкция биарки
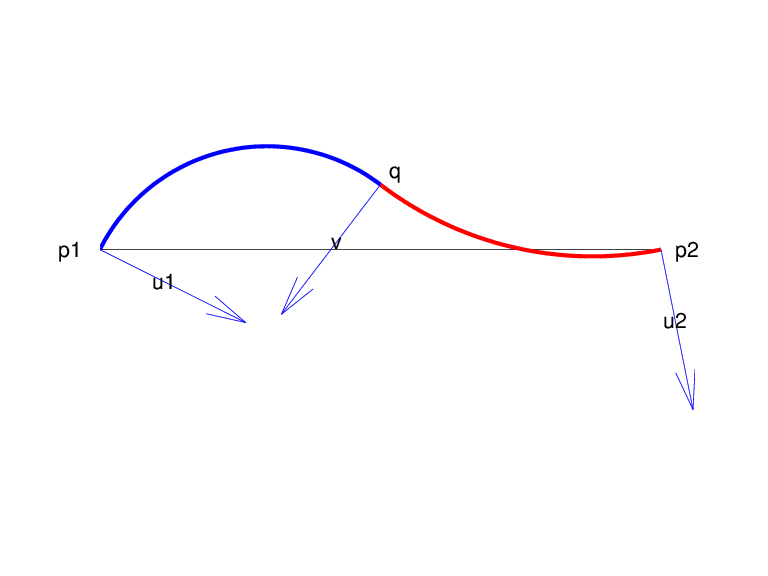
Учитывая две разные точки, p1 и p2, в плоскости и, соответственно, двух ненулевых векторов, u1 и u2, существует однопараметрическое семейство биарков (т.е. кривая, состоящая из двух дуг с общим тангенсом при их соединении), начиная с p1 и нормально там, чтобы u1 и заканчивается на p2 и нормально там, чтобы u2. Один из способов параметризовать это семейство биарков - это нормальное направление, v, в точке q с которой соединяются две дуги. С ненулевым v выбран, тогда есть только один выбор qпоэтому затем определяется вся биарка. В конструкции, используемой в rscvn, v выбран в качестве отражения перпендикулярно сегменту от p1 на p2, от среднего значения векторов u1 и u2, - после того, как оба вектора были настолько нормированы, что их длина равна 1 и что они оба указывают справа от сегмента от p1 на p2. Этот выбор для v представляется естественным в двух стандартных случаях: (i) u2 является отражением u1 перпендикулярно сегменту от p1 на p2; (ii) u1 и u2 являются параллельными. Этот выбор v подтверждается Biarcs как функция левого нормаля, которая показывает получившиеся биарки при p1, p2, и u2 = [.809;.588]сохраняются фиксированными и только нормальными при p1 разрешено изменять.
Смещения как функция левого нормаля

Но невозможно, чтобы интерполяционная биарка постоянно зависела от всех четырех данных p1, p2, u1, u2. Должно быть разрыв как нормальные направления, u1 и u2, пройти через направление от p1 на p2. Это проиллюстрировано в Biarcs как функция одной конечной точки, которая показывает биарки, когда одна точка, p1 = [0;0]и двух нормалей, u1 = [1;1] и u2 = [1;-1], удерживаются фиксированными и только другие точки, p2, перемещается, по кругу вокруг p1.
Biarcs как функция одной конечной точки
