Сглаживание сплайнов

Сведения о сглаживании сплайнов

Если ваши данные зашумлены, можно подогнать их с помощью сглаживающего сплайна. Кроме того, можно использовать один из методов сглаживания, описанных в данных фильтрации и сглаживания.

Сглаживающий сплайн s построен для заданного параметра сглаживания p и заданных весов _wi. Сглаживающий сплайн минимизирует

$p {\sum_{i} w_{i} {(y_{i} - s (x_{i}))}^{2} + (1 - p) \int (\frac{d^{2} s}{d x^{2}})}^{2} d x$

Если веса не заданы, они приняты равными 1 для всех точек данных.

p определяется между 0 и 1. p = 0 создает прямолинейную подгонку методом наименьших квадратов к данным, в то время как p = 1 создает кубическую сплайн интерполяцию. Если вы не задаете параметр сглаживания, он автоматически выбирается в «интересной области значений». Интересная область значений p часто близка к 1/( 1 + h³/ 6) где h - средний интервал между точками данных, и он обычно намного меньше допустимой области значений параметра. Поскольку сглаживающие сплайны имеют связанный параметр сглаживания, можно считать, что эти подгонки являются параметрическими в этом смысле. Однако сглаживающие сплайны также кусочные полиномы как кубический сплайн или сохраняющие форму интерполяции и считаются непараметрическим типом подгонки в этом руководстве.

Примечание

Алгоритм сглаживания сплайна основан на csaps функция.

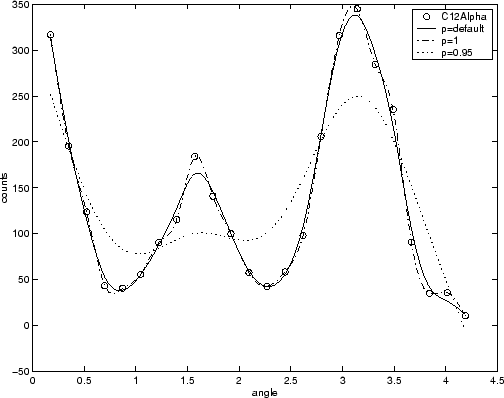
Данные ядерной реакции из файла carbon12alpha.mat показаны здесь с тремя сглаживающими сплайновыми подгонка. Параметр сглаживания по умолчанию (p = 0,99) приводит к самой гладкой кривой. Кубическая сплайн (p = 1) проходит через все точки данных, но не так гладко. Третья кривая (p = 0,95) пропускает данные с большим запасом и иллюстрирует, насколько маленьким может быть «интересная область значений» p.

Интерактивный выбор сглаживающего сплайна

В приложении Аппроксимирование Кривыми выберите Smoothing Spline из списка типов модели.

Можно задать следующие опции:

Чтобы сделать более плавную подгонку дальше от данных, неоднократно нажимайте кнопку < Smoother, пока график не покажет нужную плавность.
Чтобы сделать более грубую подгонку ближе к данным, нажмите кнопку Rougher >, пока вы не будете удовлетворены графиком.
Также задайте любое значение от 0 до 1 для параметра сглаживания. 0 создает линейную аппроксимацию полиномом (прямолинейную подгонку методом наименьших квадратов к данным), в то время как 1 производит кусочно-кубическую аппроксимацию полиномом, которая проходит через все точки данных (кубическая сплайн интерполяция).
Щелкните Default, чтобы вернуться к начальному значению. Тулбокс пытается выбрать значение по умолчанию, соответствующее вашим данным. См. «Сведения о сглаживании сплайнов».

Для примера:

Загрузите данные в разделе «Сведения о сглаживании сплайнов» путем ввода:
```
load carbon12alpha
```
В приложении Аппроксимирование Кривыми выберите angle для X data и counts для Y data.
Выберите Smoothing Spline тип аппроксимации.
Попробуйте сглаживать значения параметров 1, 0.95и значение по умолчанию (0,99).

Подгонка сглаживания Сплайна Моделей с использованием `fit` Функция

Открыть Live Script

В этом примере показано, как использовать fit функция для подгонки сглаживающей сплайн модели к данным.

Подбор сглаживающей модели сплайна

Загрузите данные и подгоните сглаживающую модель сплайна путем определения 'smoothingspline' при вызове функции подгонки.

load enso
f = fit(month,pressure,'smoothingspline');
plot(f,month,pressure)

Figure contains an axes. The axes contains 2 objects of type line. These objects represent data, fitted curve.

Просмотр вычисленного параметра сглаживания

Создайте модель снова и используйте третий выходной аргумент, чтобы просмотреть вычисленный параметр сглаживания. Параметр сглаживания является p значение в out структура. Значение по умолчанию зависит от набора данных.

[f,gof,out] = fit(month,pressure,'smoothingspline');

out.p

ans = 0.9000

Задайте параметр сглаживания используя 'SmoothingParam'

Задайте параметр сглаживания для новой подгонки с 'SmoothingParam' опция. Его значение должно быть от 0 до 1.

f = fit(month,pressure,'smoothingspline','SmoothingParam',0.07);
plot(f,month,pressure)

Figure contains an axes. The axes contains 2 objects of type line. These objects represent data, fitted curve.

Задайте параметр сглаживания используя fitoptions

Кроме того, используйте fitoptions чтобы задать параметр сглаживания перед подбором кривой.

options = fitoptions('Method','Smooth','SmoothingParam',0.07);
[f,gof,out] = fit(month,pressure,'smooth',options);
out.p

ans = 0.0700

Для альтернативы 'smoothingspline', можно использовать csaps кубическую функцию сглаживания сплайна или другие функции сплайна, которые позволяют больше контролировать то, что можно создать. См. «Сведения о сплайнах» в наборе инструментов Curve Fitting Toolbox.

Пример: Непараметрический подбор кривой с кубическими и сглаживающими сплайнами

Этот пример подходит для некоторых данных с помощью кубической сплайн интерполяции и нескольких сглаживающих сплайнов.

Создайте переменные в вашей рабочей области:
```
x = (4*pi)*[0 1 rand(1,25)]; 
y = sin(x) + .2*(rand(size(x))-.5);
```
Откройте приложение Аппроксимирование Кривыми, введя:
```
cftool
```
Выберите x и y из X data и Y data списков.
Приложение Аппроксимирование Кривыми подходит и строит графики данных.
Подгонка данных с помощью кубической сплайн интерполяции путем выбора типа Interpolant и Method Cubic.
Приложение Аппроксимирование Кривыми подходит и строит графики кубической сплайн интерполяции.
Введите Fit name cubicsp.
Просмотр панели Results. Статистика качества подгонки, такая как RMSE, не определена (показана как NaN) для интерполяций.
Кубическая сплайн интерполяция определяется как кусочный полином, которая приводит к структуре коэффициентов (p). Количество «частей» в структуре на один меньше, чем количество подгоняемых точек данных, и количество коэффициентов для каждой части равняется четырем, потому что полиномиальная степень равна трем. Можно изучить структуру коэффициентов p если вы экспортируете свою подгонку в рабочую область (например, вводите fitname.p). Для получения информации о структуре коэффициентов смотрите Построение и Работа со сплайнами ppform.
Создайте другую подгонку для сравнения. Щелкните правой кнопкой мыши подгонку в Table of Fits и выберите Duplicate ‘cubicsp’.
Подгонка данных к сглаживающему сплайну осуществляется путем выбора Smoothing Spline.
Уровень плавности задается параметром Сглаживания. Сглаживание по умолчанию значения параметров зависит от набора данных и автоматически вычисляется тулбоксом.
Для этого набора данных параметр сглаживания по умолчанию близок к 1, что указывает на то, что сглаживающий сплайн является почти кубическим и близок к прохождению через каждую точку данных.
Назовите параметр сглаживания по умолчанию подгонки Smooth1. Если вам не нравится уровень сглаживания, произведенный параметром сглаживания по умолчанию, можно задать любое значение от 0 до 1. 0 создает линейную аппроксимацию полиномом, в то время как 1 создает кусочно-кубическую аппроксимацию полиномом, которая проходит через все точки данных.
Числовые результаты сглаживания сплайна подгонки показаны здесь.
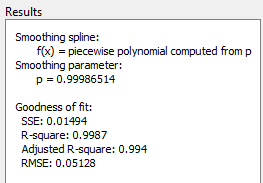
Для сравнения создайте еще один сглаживающий сплайн подгонки. Щелкните правой кнопкой мыши подгонку в Table of Fits и выберите Duplicate ‘smooth1’. Измените параметр сглаживания на 0.5 и назовите Smooth2 подгонки.
Сравните графики для ваших трех подгонка. Исследуйте поведение подгонки за пределами данных путем увеличения шкалы абсциссы по умолчанию. Пределы осей можно изменить с помощью Tools > Axes Limit Control элемента меню.

Примечание

Ваши результаты зависят от случайных начальных точек и могут отличаться от описанных.

Обратите внимание, что параметр сглаживания по умолчанию создает кривую, которая более гладкая, чем интерполяция, но является хорошей подгонкой к данным. В этом случае уменьшение параметра сглаживания от значения по умолчанию создает кривую, которая все еще сглаживается, но не является хорошей подгонкой к данным. Когда параметр сглаживания увеличивается сверх значения по умолчанию, связанная кривая приближается к кубической сплайн интерполяции. Кубический сплайн и сплайн сглаживания по умолчанию аналогичны для внутренних точек, но различаются в конечных точках.

См. также

fit

Документация