Вы можете использовать smooth функция для сглаживания данных отклика. Можно использовать дополнительные методы для скользящего среднего значения, фильтров Савицкого-Голея и локальной регрессии с весами и робастностью и без них (lowess, loess, rlowess и rloess).
Фильтр скользящего среднего сглаживает данные путем замены каждой точки данных средним значением соседних точек данных, определенных в пределах диапазона. Этот процесс эквивалентен lowpass с откликом сглаживания, заданным разностным уравнением
где ys (i) - сглаженное значение для ith data point, N является количеством соседних точек данных с каждой стороны ys (i), и 2 N + 1 является диапазоном.
Метод сглаживания скользящего среднего, используемый Curve Fitting Toolbox™, следует этим правилам:
Размах должен быть нечетным.
Сглаживаемая точка данных должна находиться в центре диапазона.
Диапазон скорректирован для точек данных, которые не могут вместить указанное количество соседей с обеих сторон.
Конечные точки не сглаживаются, поскольку невозможно задать диапазон.
Обратите внимание, что вы можете использовать filter функция для реализации разностных уравнений, таких как показанное выше. Однако из-за того, как обрабатываются конечные точки, результат скользящего среднего тулбокса будет отличаться от результата, возвращенного filter. Для получения дополнительной информации см. раздел «Разностные уравнения и фильтрация».
Например, предположим, что вы сглаживаете данные с помощью фильтра скользящего среднего с диапазоном 5. Используя описанные выше правила, первые четыре элемента ys даны
ys(1) = y(1) ys(2) = (y(1)+y(2)+y(3))/3 ys(3) = (y(1)+y(2)+y(3)+y(4)+y(5))/5 ys(4) = (y(2)+y(3)+y(4)+y(5)+y(6))/5
Обратите внимание, что ys (1), ys (2)..., ys (end) см. порядок данных после сортировки, и не обязательно исходный порядок.
Сглаженные значения и диапазоны для первых четырех точек данных сгенерированного набора данных показаны ниже.
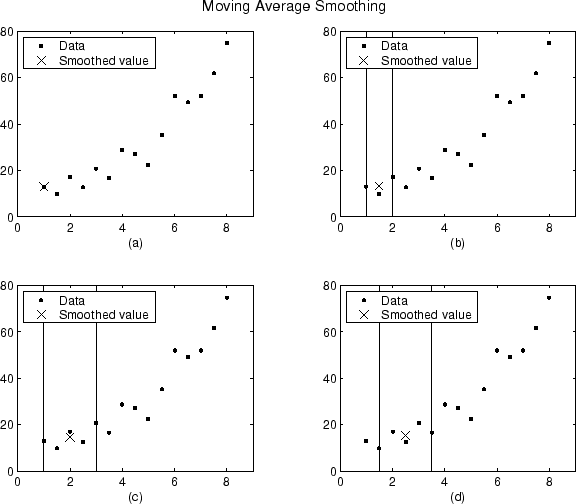
График (a) указывает, что первая точка данных не сглажена, поскольку не удается создать диапазон. График (b) указывает, что вторая точка данных сглаживается с помощью диапазона из трех. Графики (c) и (d) указать, что для вычисления сглаженного значения используется диапазон пять.
Фильтрация Савицкого-Голея может рассматриваться как обобщённое скользящее среднее значение. Вы выводите коэффициенты фильтра, выполняя невзвешенный линейный метод наименьших квадратов подгонки используя полином заданной степени. По этой причине фильтр Савицкого-Голея также называется цифровым полиномиальным фильтром сглаживания или фильтром сглаживания методом наименьших квадратов. Обратите внимание, что полином более высокой степени позволяет достичь высокого уровня сглаживания без ослабления функций данных.
Метод фильтрации Савицкого-Голая часто используется с частотными данными или со спектроскопическими (пиковыми) данными. Для частотных данных метод эффективен при сохранении высокочастотных компонентов сигнала. Для спектроскопических данных метод эффективен при сохранении более высоких моментов пика, таких как ширина линии. Для сравнения, фильтр скользящего среднего имеет тенденцию отфильтровывать значительный фрагмент высокочастотного содержимого сигнала, и он может только сохранять более низкие моменты пика, такого как центроид. Однако фильтрация Савицкого-Голея может быть менее успешной, чем фильтр скользящего среднего при отказе от шума.
Метод сглаживания Савицкого-Голея, используемый программным обеспечением Curve Fitting Toolbox, следует этим правилам:
Размах должен быть нечетным.
Полиномиальная степень должна быть меньше, чем диапазон.
Точки данных не должны иметь одинаковые интервалы.
Обычно фильтрация Савицкого-Голея требует равномерного интервала между данными предиктора. Однако алгоритм Curve Fitting Toolbox поддерживает неоднородные интервалы. Поэтому вы не обязаны выполнять дополнительный шаг фильтрации для создания данных с равномерным интервалом.
На графике, показанном ниже, отображаются сгенерированные Гауссовы данные и несколько попыток сглаживания с помощью метода Савицкого-Голая. Данные являются очень шумными, и ширины пиков варьируются от широких до узких. Диапазон равен 5% от количества точек данных.
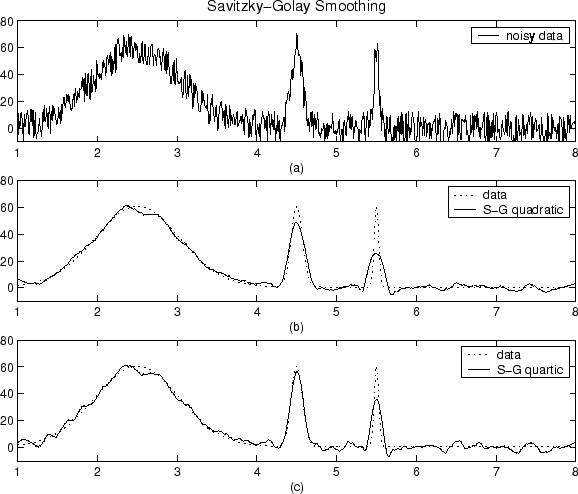
График (a) показывает зашумленные данные. Чтобы легче сравнить сглаженные результаты, графики (b) и (c) показать данные без добавленного шума.
График (b) показывает результат сглаживания квадратичным полиномом. Заметьте, что метод плохо работает для узкого peaks. График (c) показывает результат сглаживания с помощью квартального полинома. В целом полиномы более высокой степени могут более точно захватывать высоты и ширины узкого peaks, но могут плохо справляться с сглаживанием более широкого peaks.
Имена «lowess» и «loess» получают из термина «локально взвешенный график поля точек гладкий», поскольку оба метода используют локально взвешенную линейную регрессию для сглаживания данных.
Процесс сглаживания рассматривается локальным, потому что, как и метод скользящего среднего, каждое сглаженное значение определяется соседними точками данных, заданными в пределах диапазона. Процесс взвешивается, потому что для точек данных, содержащихся в диапазоне, задана функция веса регрессии. В дополнение к функции регрессионного веса можно использовать устойчивую функцию веса, которая делает процесс устойчивым к выбросам. Наконец, методы дифференцируются моделью, используемой в регрессии: lowess использует линейный полином, в то время как loess использует квадратичный полином.
Методы локального регрессионного сглаживания, используемые программным обеспечением Curve Fitting Toolbox, следуют следующим правилам:
Размах может быть четным или нечетным.
Диапазон можно задать как процент от общего количества точек данных в наборе данных. Для примера диапазон 0,1 использует 10% точек данных.
Процесс сглаживания локальной регрессии следует этим шагам для каждой точки данных:
Вычислите веса регрессии для каждой точки данных в диапазоне. Веса заданы функцией трикуба, показанной ниже.
x - значение предиктора, сопоставленное со значением отклика, которое будет сглаживаться, xi являются ближайшими соседями x, как определено диапазоном, и d (x) - это расстояние вдоль абсциссы от x до наиболее удаленного значения предиктора в интервале. Веса имеют следующие характеристики :
Сглаживаемая точка данных имеет наибольший вес и наибольшее влияние на подгонку.
Точки данных за пределами диапазона имеют нулевой вес и не влияют на подгонку.
Выполняется взвешенная регрессия линейного метода наименьших квадратов. Для lowess в регрессии используется полином первой степени. Для loess в регрессии используется полином второй степени.
Сглаженное значение задается взвешенной регрессией при значении предиктора интереса.
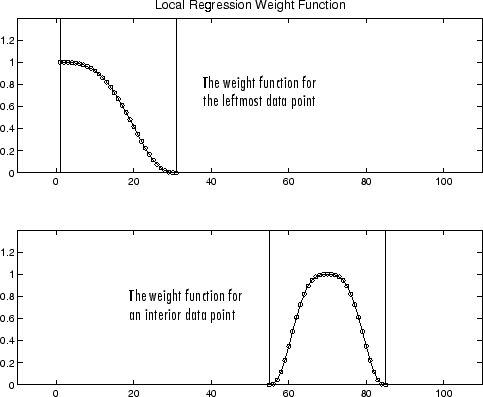
Если в плавном вычислении участвует то же количество соседних точек данных с каждой стороны сглаженной точки данных, весовая функция симметрична. Однако, если количество соседних точек не симметрично относительно сглаженной точки данных, то весовая функция не симметрична. Обратите внимание, что в отличие от процесса сглаживания скользящего среднего, диапазон никогда не меняется. Например, когда вы сглаживаете точку данных с наименьшим значением предиктора, форма функции веса усекается на половину, самая левая точка данных в диапазоне имеет самый большой вес, и все соседние точки находятся справа от сглаженного значения.
Функция веса для конечной точки и для внутренней точки показана ниже для диапазона 31 точки данных.
Используя метод lowess с диапазоном пять, сглаженные значения и связанные регрессии для первых четырех точек данных сгенерированного набора данных показаны ниже.
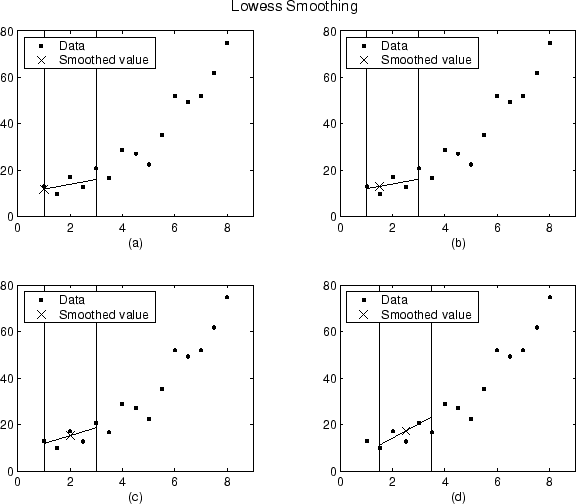
Заметьте, что диапазон не меняется, когда процесс сглаживания прогрессирует от точки данных к точке данных. Однако, в зависимости от количества ближайших соседей, функция регрессионного веса может не быть симметричной относительно точки данных, которая будет сглажена. В частности, графики (a) и (b) используйте асимметричную функцию веса, в то время как графики (c) и (d) используйте симметричную весовую функцию.
Для метода loess графиков будут выглядеть одинаково, за исключением того, что сглаженное значение будет сгенерировано полиномом второй степени.
Если ваши данные содержат выбросы, сглаженные значения могут стать искаженными, а не отражать поведение большей части соседних точек данных. Чтобы преодолеть эту проблему, можно сгладить данные с помощью устойчивой процедуры, на которую не влияет небольшая часть выбросов. Описание выбросов см. в разделе «Остаточный анализ».
Программное обеспечение Curve Fitting Toolbox обеспечивает устойчивую версию как для методов lowess, так и для сглаживания лессов. Эти устойчивые методы включают дополнительное вычисление устойчивых весов, которые устойчивы к выбросам. Устойчивая процедура сглаживания выполняется на следующих этапах:
Вычислите невязки от процедуры сглаживания, описанной в предыдущем разделе.
Вычислите устойчивые веса для каждой точки данных в диапазоне. Веса задаются функцией bisquare,
где ri - невязка i-й точки данных, произведенный процедурой регрессионного сглаживания, и MAD - медианное абсолютное отклонение невязок,
Срединное абсолютное отклонение является мерой того, как распределены невязки. Если ri маленькая по сравнению с 6 MAD, то устойчивый вес близок к 1. Если ri больше 6 MAD, устойчивый вес 0, и связанная точка данных исключается из плавного вычисления.
Сглаживайте данные снова, используя устойчивые веса. Окончательное сглаженное значение вычисляют, используя как локальный регрессионный вес, так и устойчивый вес.
Повторите два предыдущих шага для пяти итераций.
Результаты сглаживания процедуры lowess сравниваются ниже с результатами процедуры устойчивой lowess для сгенерированного набора данных, который содержит один выбросы. Диапазон для обеих процедур составляет 11 точек данных.
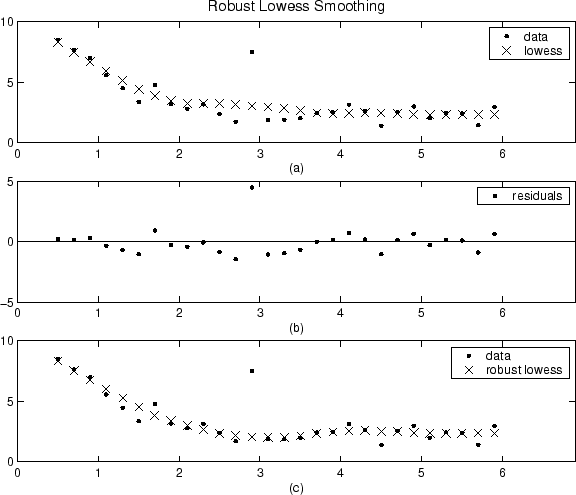
График (a) показывает, что выбросы влияют на сглаженное значение для нескольких ближайших соседей. График (b) предполагает, что невязка выбросов больше шести медианных абсолютных отклонений. Поэтому устойчивый вес равен нулю для этой точки данных. График (c) показывает, что сглаженные значения, соседствующие с выбросами, отражают основную часть данных.
Загрузите данные в count.dat:
load count.dat
Массив 24 на 3 count содержит количество трафика на трех перекрестках для каждого часа дня.
Во-первых, используйте фильтр скользящего среднего с 5-часовым диапазоном, чтобы сгладить все данные сразу (по линейному индексу):
c = smooth(count(:)); C1 = reshape(c,24,3);
Постройте график исходных данных и сглаженных данных:
subplot(3,1,1)
plot(count,':');
hold on
plot(C1,'-');
title('Smooth C1 (All Data)')Во-вторых, используйте тот же фильтр, чтобы сглаживать каждый столбец данных отдельно:
C2 = zeros(24,3);
for I = 1:3,
C2(:,I) = smooth(count(:,I));
endСнова постройте график исходных данных и сглаженных данных:
subplot(3,1,2)
plot(count,':');
hold on
plot(C2,'-');
title('Smooth C2 (Each Column)')Постройте график различия между двумя сглаженными наборами данных:
subplot(3,1,3)
plot(C2 - C1,'o-')
title('Difference C2 - C1')
Обратите внимание на дополнительные эффекты разглаживания 3-х столбцов.
Создайте зашумленные данные с выбросами:
x = 15*rand(150,1); y = sin(x) + 0.5*(rand(size(x))-0.5); y(ceil(length(x)*rand(2,1))) = 3;
Сглаживайте данные, используя loess и rloess методы с размахом 10%:
yy1 = smooth(x,y,0.1,'loess'); yy2 = smooth(x,y,0.1,'rloess');
Постройте график исходных данных и сглаженных данных.
[xx,ind] = sort(x);
subplot(2,1,1)
plot(xx,y(ind),'b.',xx,yy1(ind),'r-')
set(gca,'YLim',[-1.5 3.5])
legend('Original Data','Smoothed Data Using ''loess''',...
'Location','NW')
subplot(2,1,2)
plot(xx,y(ind),'b.',xx,yy2(ind),'r-')
set(gca,'YLim',[-1.5 3.5])
legend('Original Data','Smoothed Data Using ''rloess''',...
'Location','NW')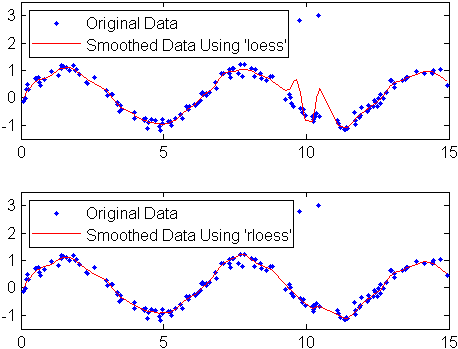
Обратите внимание, что выбросы оказывают меньшее влияние на устойчивый метод.