Exponenta Banner

atan2

Обратный тангенс с четырьмя квадрантами значений с фиксированной точкой

Свернуть все на странице

Синтаксис

z = atan2(y,x)

Описание

пример

z = atan2(y,x) возвращает arctangent с четырьмя квадрантами fi входы y и x.

Примеры

свернуть все

Открыть Live Script

Используйте atan2 функция для вычисления арктангенса беззнаковых и со знаком с фиксированной точкой входных значений.

Неподписанные входные значения

В этом примере используются беззнаковые 16-битные значения размера слова.

y = fi(0.125,0,16);
x = fi(0.5,0,16);  
z = atan2(y,x)
z = 
    0.2450

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Unsigned
            WordLength: 16
        FractionLength: 15

Подписанные входные значения

В этом примере используются 16-битные значения размера слова со знаком.

y = fi(-0.1,1,16);
x = fi(-0.9,1,16);  
z = atan2(y,x)
z = 
   -3.0309

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 13

Входные параметры

свернуть все

y-координаты, заданные как скалярный, векторный, матричный или многомерный массив.

y и x могут быть действительными, подписанными или беззнаковыми скалярами, векторами, матрицами или N-мерные массивы, содержащие значения угла с фиксированной точкой в радианах. Входы y и x должен быть одинаковым размером. Если они не совпадают по размеру, по крайней мере, один вход должен быть скалярным значением. Допустимые типы данных y и x являются:

  • fi одинок

  • fi дважды

  • fi фиксированная точка с двоичным масштабированием точек

  • fi масштабированный двойной с двоичным масштабированием точек

Типы данных: fi

x-координаты, заданные как скалярный, векторный, матричный или многомерный массив.

y и x могут быть действительными, подписанными или беззнаковыми скалярами, векторами, матрицами или N-мерные массивы, содержащие значения угла с фиксированной точкой в радианах. Входы y и x должен быть одинаковым размером. Если они не совпадают по размеру, по крайней мере, один вход должен быть скалярным значением. Допустимые типы данных y и x являются:

  • fi одинок

  • fi дважды

  • fi фиксированная точка с двоичным масштабированием точек

  • fi масштабированный двойной с двоичным масштабированием точек

Типы данных: fi

Выходные аргументы

свернуть все

Четырехквадрантный арктангенс, возвращенный как скалярный, векторный, матричный или многомерный массив.

z - четырехквадрантный арктангенс y и x. The numerictype от z зависит от сигнальности y и x:

  • Если либо y или x подписывается, затем z - номер со знаком с фиксированной точкой в области значений [-pi, pi]. Он имеет 16-битный размер слова и 13-битную длину дроби (numerictype(1,16,13)).

  • Если оба y и x являются беззнаковыми, затем z - беззнаковый номер с фиксированной точкой в область значений [0, pi/2]. Он имеет 16-битный размер слова и 15-битную длину дроби (numerictype(0,16,15)).

Выход, z, всегда сопоставляется со значением по умолчанию fimath.

Подробнее о

свернуть все

Четырёхквадрантный арктангенс

Четырехквадрантный арктангенс определяется следующим образом относительно atan функция:

atan2(y,x)={atan(yx)            x>0π+atan(yx)      y≥0,x<0−π+atan(yx)    y<0,x<0π2                        y>0,x=0−π2                      y<0,x=00                          y=0,x=0

Алгоритмы

свернуть все

atan2 функция вычисляет arctangent с четырьмя квадрантами входных входов с фиксированной точкой с помощью 8-битной интерполяционной таблицы следующим образом:

  1. Разделите входные абсолютные значения, чтобы получить беззнаковое, дробное, с фиксированной точкой, 16-битное отношение между 0 и 1. Абсолютные значения y и x определяют, какое значение является делителем.

    Знаки y и x входы определяют, в каком квадранте лежит их отношение. Вход с большим абсолютным значением используется в качестве знаменателя, таким образом получая значение от 0 до 1.

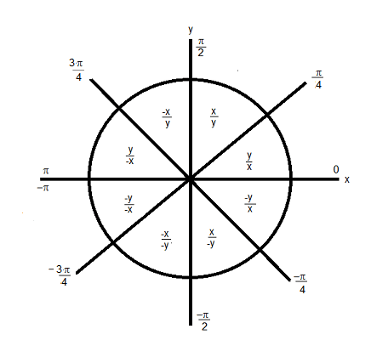
  2. Вычислите индекс таблицы на основе 16-битного, беззнакового, сохраненного целого значения:

    1. Используйте 8 наиболее значимых битов, чтобы получить первое значение из таблицы.

    2. Используйте значение таблицы следующего большего размера в качестве второго значения.

  3. Используйте 8 младших битов для интерполяции между первым и вторым значениями с помощью самой близкой соседней линейной интерполяции. Эта интерполяция создает значение в области значений [0, pi/4).

  4. Выполните октантную коррекцию полученного угла, основанную на значениях исходной y и x входы.

Это вычисление арктангенса точно только для верхних 16 наиболее значимых битов входа.

Правила распространения fimath

The atan2 функция игнорирует и отбрасывает любые fimath присоединен к входам. Выход, z, всегда сопоставляется со значением по умолчанию fimath.

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®

.

См. также

| | | |

Темы

Введенный в R2012a

Документация Fixed-Point Designer

Поддержка