Идентифицируйте передаточные функции низкого порядка (модели процесса) с помощью Системы идентификации приложения

Введение

Цели

Оцените и проверьте простые передаточные функции в непрерывном времени из данных SISO, чтобы найти ту, которая лучше всего описывает динамику системы.

После завершения этого руководства вы сможете выполнить следующие задачи с помощью приложения Система Идентификации:

Импорт объектов данных из MATLAB^® рабочая область в приложение.
Постройте и обработайте данные.
Оцените и проверьте модели низкого порядка и непрерывного времени из данных.
Экспорт моделей в рабочее пространство MATLAB.
Симулируйте модель с помощью Simulink^® программное обеспечение.

Примечание

Это руководство использует данные временной области, чтобы продемонстрировать, как вы можете оценить линейные модели. Тот же процесс применяется к подгонке данных частотного диапазона.

Описание данных

В этом руководстве используется файл данных proc_data.mat, который содержит 200 выборок моделируемых данных временной области с одним входом/одним выходом (SISO). Входной вход является случайным двоичным сигналом, который колеблется между -1 и 1. Белый шум (соответствующий нарушению порядка нагрузки) добавляется к входу со стандартным отклонением 0,2, что приводит к отношению сигнал/шум около 20 дБ. Эти данные моделируются с помощью системы второго порядка с недостаточно демпфированными режимами (комплексные полюсы) и максимальной чувствительностью с частотой 1 рад/с:

$G (s) = \frac{1}{1 + 0.2 s + s^{2}} e^{- 2 s}$

Шаг расчета симуляции составляет 1 секунду.

Что такое модель процесса непрерывного времени?

Модели процесса в непрерывном времени являются передаточными функциями низкого порядка, которые описывают динамику системы с помощью статического усиления, временной задержкой перед выходом системы на вход и характерными временными константами, связанными с полюсами и нулями. Такие модели популярны в индустрии и часто используются для настройки ПИД-регуляторов, для примера. Параметры модели процесса имеют физическую значимость.

Можно задать различные структуры модели процесса путем изменения количества полюсов, добавления интегратора или включения временной задержки или нуля. Самый высокий порядок модели процесса, который вы можете задать в этом тулбоксе, равен трем, и полюса могут быть реальными или сложными (режимы с недостаточным демпфированием).

В целом линейная система характеризуется передаточной функцией G, которая является оператором, который переводит вход u в выход y:

$y = G u$

Для системы в непрерывном времени G связывает преобразования Лапласа входных U (s) и выходных Y (s) следующим образом:

$Y (s) = G (s) U (s)$

В этом руководстве вы оцениваете G, используя различные структуры модели процесса.

Например, следующая структура модели является моделью первого порядка в непрерывном времени, где K является статическим усилением, _Tp1 является временной константой, и _Td является задержкой ввода-вывода:

$G (s) = \frac{K}{1 + s T_{p 1}} e^{- s T_{d}}$

Подготовка данных к системе идентификации

Загрузка данных в рабочее пространство MATLAB

Загрузите данные в proc_data.mat путем ввода следующей команды в Командном Окне MATLAB:

load proc_data

Эта команда загружает данные в рабочее пространство MATLAB в качестве объекта данных z. Для получения дополнительной информации о iddata объекты соответствующую страницу с описанием.

Открытие Системы идентификации приложения

Чтобы открыть приложение System Identification, введите следующую команду в Командном окне MATLAB:

systemIdentification

Имя сеанса по умолчанию, Untitled, появляется в строке заголовка.

Импорт объектов данных в приложение Системы идентификации

Можно импортировать объект данных в приложение из рабочего пространства MATLAB.

Вы, должно быть, уже загрузили выборочные данные в MATLAB, как описано в Загрузке данных в рабочее пространство MATLAB, и открыли приложение, как описано в Открытии приложения для системы идентификации.

Если вы не выполнили эти шаги, щелкните здесь, чтобы завершить их.

Чтобы импортировать объект данных в приложение Системы идентификации:

Выберите Import data > Data object.
Это действие открывает диалоговое окно Импорт данных.
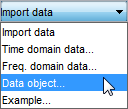
В диалоговом окне «Импорт данных» задайте следующие опции:
- Object - Ввод z как имя переменного MATLAB, которая является объектом данных во временной области. Нажмите Enter.
- Data name - Используйте имя по умолчанию z, то же, что и имя объекта данных, который вы импортами. Это имя помечает данные в приложении Системы идентификации после завершения операции импорта.
- Starting time - Ввод 0 как время запуска. Это значение определяет начальное значение оси времени на временных графиках.
- Sample time - Ввод 1 как время между последовательными выборками в секундах. Это значение представляет фактический шаг расчета в эксперименте.
Диалоговое окно Импорт данных теперь напоминает следующий рисунок.
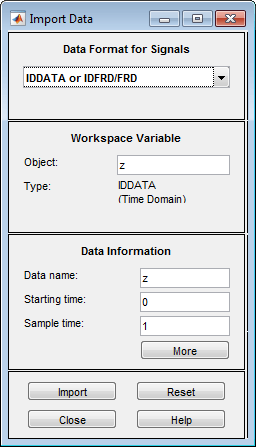
Нажмите Import, чтобы добавить данные к приложению Системы идентификации. Приложение добавляет значок, чтобы представлять данные.
Нажмите кнопку Close, чтобы закрыть диалоговое окно Импорт данных.

Графическое изображение и обработка данных

В этом фрагменте руководства вы оцениваете данные и обрабатываете их для системы идентификации. Вы узнаете, как:

Постройте график данных.
Удалите смещения путем вычитания средних значений входа и выхода.
Разделите данные на две части. Вы используете одну часть данных для оценки модели, а другую часть данных для валидации модели.

Причина, по которой вы вычитаете средние значения из каждого сигнала, заключается в том, что, как правило, вы создаете линейные модели, которые описывают отклики на отклонения от физического равновесия. С помощью статических данных разумно предположить, что средние уровни сигналов соответствуют такому равновесию. Таким образом, можно искать модели около нуля, не моделируя абсолютные равновесные уровни в физических единицах измерения.

Вы должны уже импортировать данные в приложение Системы идентификации, как описано в разделе Импорт объектов данных в приложение Системе идентификации.

Если вы не выполнили этот шаг, щелкните здесь, чтобы завершить его.

Чтобы построить и обработать данные:

Установите флажок Time plot, чтобы открыть окно Time Plot.
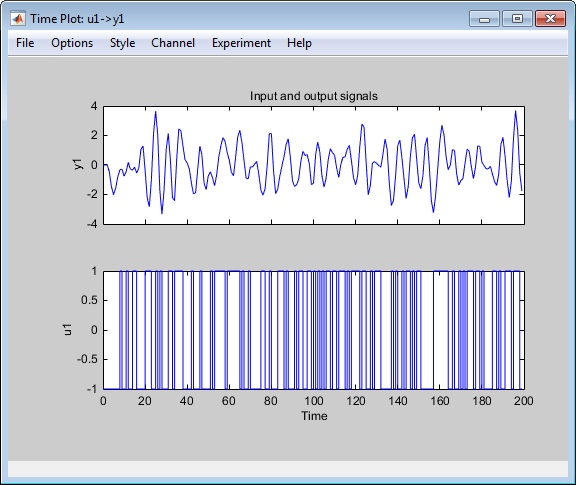
Нижние оси показывают входные данные - случайную двоичную последовательность, а верхние - выходные данные.
Следующие два шага демонстрируют, как изменить пределы по осям на графике.
Чтобы изменить пределы по вертикали для входных данных, выберите Options > Set axes limits в окно рисунка Time Графика.
В диалоговом окне Limits for Time Plot установите новый предел по вертикальной оси входного канала данных u1 равный [-1,5 1,5]. Нажмите Apply и Close.

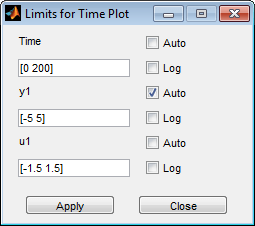
Примечание
Другие два поля в диалоговом окне Limits for Time Plot, Time и y1, позволяют вам задать пределы по осям для оси времени и оси выходного канала, соответственно. Можно также задать каждую ось, которая будет логарифмической или линейной, выбрав соответствующую опцию.
Следующий рисунок показывает обновленный график времени.
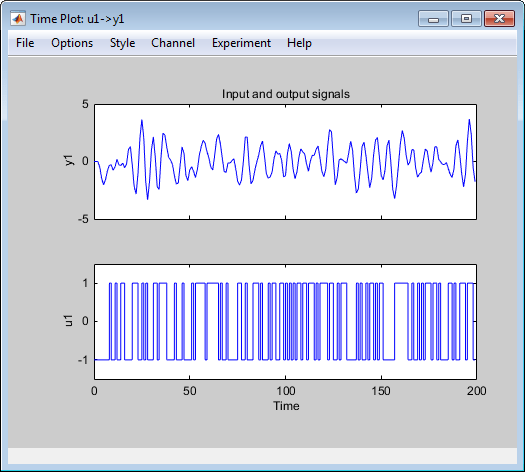
В приложении System Identification выберите <--Preprocess > Quick start, чтобы выполнить следующие четыре действия:
- Вычесть среднее значение из каждого канала.
- Разделите данные на две части.
- Определите первую часть данных как данные оценки (или Working Data).
- Укажите вторую часть данных следующим Validation Data.

Подробнее. Для получения информации о поддерживаемых операциях обработки данных, таких как повторная дискретизация и фильтрация данных, см. Раздел «Предварительная обработка данных».

Оценка передаточной функции второго порядка (модель процесса) со сложными полюсами

Оценка передаточной функции второго порядка с использованием настроек по умолчанию

В этом фрагменте руководства вы оцениваете модели с этой структурой:

$G (s) = \frac{K}{(1 + 2 ξ T_{w} s + T_{w}^{2} s^{2})} e^{- T_{d} s}$

Вы должны уже обработать данные для оценки, как описано в Графическое изображение и Обработка данных.

Если вы не выполнили этот шаг, щелкните здесь, чтобы завершить его.

Для идентификации передаточной функции второго порядка:

В приложении Системы идентификации выберите Estimate > Process models, чтобы открыть диалоговое окно Process Моделей.
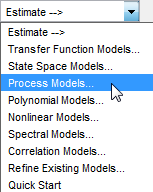
В области Model Transfer Function диалогового окна Модели процесса (Process Models) задайте следующие опции:
- В группе Poles выберите 2 и Underdamped.
  Этот выбор обновляет Передаточную Функцию Модели на структуру модели второго порядка, которая может содержать сложные полюса.
- Убедитесь, что флажки Zero и Integrator сняты, чтобы исключить из модели нуль и интегратор (саморегулирующийся).
Область Parameter диалогового окна Process Models теперь показывает четыре активных параметра: K, Tw, Zeta, и Td. В области Initial Guess сохраните значение по умолчанию Auto-selected опция для вычисления начальных значений параметров во время оценки. Столбец Initial Guess в таблице Параметра отображений Auto.
Сохраните значения Bounds по умолчанию, которые задают минимальное и максимальное значения каждого параметра.
Совет
Если вы знаете область значений возможных значений для параметра, можно ввести эти значения в соответствующие Bounds поля, чтобы помочь алгоритму оценки. Нажмите клавишу Enter после того, как вы задаете значения.
Сохраните настройки по умолчанию для алгоритма оценки:
- Disturbance Model — None означает, что алгоритм не оценивает шумовую модель. Эта опция также устанавливает Focus равной Simulation.
- Focus — Simulation означает, что алгоритм оценки не использует модель шума, чтобы взвесить относительную важность того, как тесно соответствовать данным в различных частотных областях значений. Вместо этого алгоритм использует входной спектр в конкретной частотной области значений, чтобы взвесить относительную важность подгонки в этой частотной области значений.
  Совет
  The Simulation настройка оптимизирована для идентификации моделей, которые вы планируете использовать для симуляции выхода. Если вы планируете использовать свою модель для выхода предсказания или управления приложениями, или улучшить оценки параметров с помощью модели шума, выберите Prediction.
- Initial condition — Auto означает, что алгоритм анализирует данные и выбирает оптимальный метод для обработки начального состояния системы. Если вы получаете плохие результаты, можно попробовать задать определенный метод для обработки начальных состояний, а не выбирать его автоматически.
- Covariance — Estimate означает, что алгоритм вычисляет неопределенности параметров, которые отображаются как области доверия модели на графиках.
Приложение присваивает модели имя, показанное в поле Name (находится в нижней части диалогового окна). По умолчанию имя является аббревиатурой P2DU, что указывает на два полюса (P2), задержка (D) и недостаточно демпфированные режимы (U).
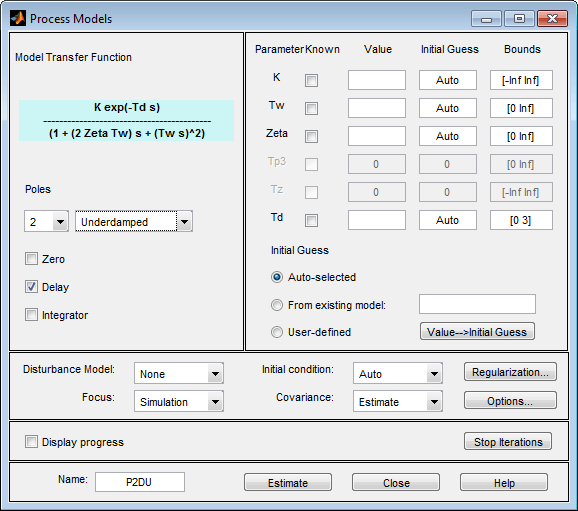
Нажмите Estimate, чтобы добавить модель P2DU в приложение Системы идентификации.

Советы по указанию известных параметров

Если вы точно знаете значение параметров, можно ввести это значение в Value столбец диалогового окна Модели процесса (Process Models). Установите соответствующий флажок Known после определения значения.

Если вы знаете приблизительное значение параметра, можно помочь алгоритму оценки, введя начальное значение в Initial Guess столбец. В этом случае оставьте флажок Known снятым, чтобы оценка могла точно настроить это начальное предположение.

Для примера, чтобы исправить значение задержки по времени Td при 2s, введите это значение в Value поле таблицы Parameter в диалоговом окне Process Models. Затем установите соответствующий флажок Known.

Валидация модели

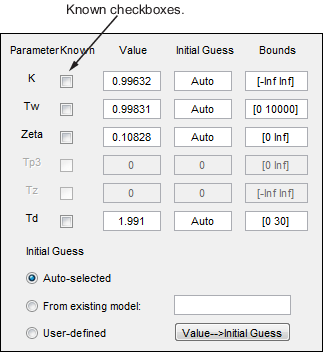
Можно проанализировать следующие графики, чтобы оценить качество модели:

Сравнение выхода модели и измеренного выхода на временном графике
Автокорреляция выходных невязок и перекрестная корреляция входных и выходных невязок

Вы должны были уже оценить модель, как описано в Оценке передаточной функции второго порядка с использованием настроек по умолчанию.

Если вы не выполнили этот шаг, щелкните здесь, чтобы завершить его.

Исследование выхода модели. Можно использовать график модель-вывод, чтобы проверить, насколько хорошо выход модели соответствует измеренному выходу в наборе данных валидации. Хорошая модель является самой простой моделью, которая лучше всего описывает динамику и успешно моделирует или предсказывает выход для различных входов.

Чтобы сгенерировать график модель-вывод, установите флажок Model output в приложении Системы идентификации. Если график пуст, щелкните значок модели в окне Системы идентификации приложения, чтобы отобразить модель на графике.

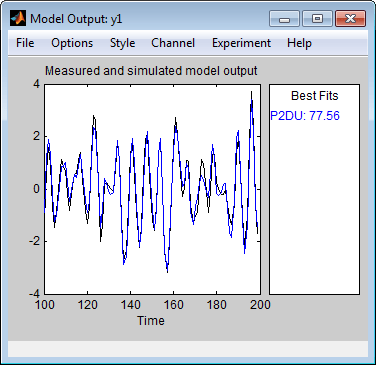
Программное обеспечение Toolbox™ идентификации системы использует данные валидации входа как входные данные для модели и строит графики моделируемых выходов на верхнюю часть из данных валидации выходов. Предыдущий график показывает, что выход модели хорошо согласуется с выходом данных валидации.

Область Best Fits графика Model Output показывает согласие (в процентах) между выходом модели и выходом данных валидации.

Напомним, что данные были моделированы с помощью следующей системы второго порядка с недостаточно демпфированными режимами (комплексные полюсы), как описано в Data Description, и имеют максимальную чувствительность 1 рад/с:

$G (s) = \frac{1}{1 + 0.2 s + s^{2}} e^{- 2 s}$

Поскольку данные включают шум на входе во время симуляции, предполагаемая модель не может точно воспроизвести модель, используемую для симуляции данных.

Исследование Невязок модели. Можно проверить модель, проверив поведение ее невязок.

Чтобы сгенерировать Остаточный График для анализа, установите флажок Model resids в приложении Системы идентификации.

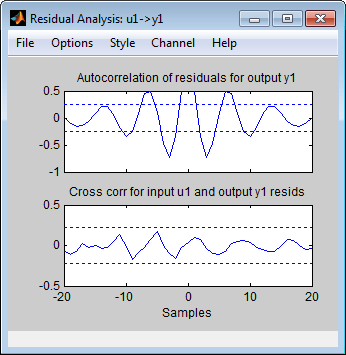
Верхние оси показывают автокорреляцию невязок для выхода (тест белизны). Горизонтальная шкала является количеством лагов, которое является временным различием (в выборки) между сигналами, в которых оценивается корреляция. Любые колебания в пределах доверия интервала считаются незначительными. Хорошая модель должна иметь остаточную автокорреляционную функцию в пределах доверия интервала, что указывает на то, что невязки некоррелированы. Однако в этом примере невязки, по-видимому, коррелируют, что естественно, потому что шумовая модель используется, чтобы сделать невязки белыми.

Нижние оси показывают перекрестную корреляцию невязок с входом. Хорошая модель должна иметь невязки, некоррелированные с прошлыми входами (тест независимости). Доказательства корреляции указывают, что модель не описывает, как фрагмент выхода относится к соответствующему входу. Для примера, когда существует пик вне интервала доверия для задержки k, это означает, что вклад в выход y (t), который происходит от входа u (t-k), не описан правильно моделью. В этом примере нет корреляции между невязками и входами.

Таким образом, остаточный анализ указывает, что эта модель хороша, но может возникнуть потребность в шумовой модели.

Оценка модели процесса с шумовым компонентом

Оценка модели процесса второго порядка со сложными полюсами

В этом фрагменте руководства вы оцениваете передаточную функцию второго порядка и включаете шумовую модель. Путем включения модели шума вы оптимизируете результаты оценки для приложения предсказания.

Если вы не выполнили этот шаг, щелкните здесь, чтобы завершить его.

Чтобы оценить передаточную функцию второго порядка с шумом:

Если диалоговое окно Модели процесса не открыто, выберите Estimate > Process Models в приложении Системе идентификации. Это действие открывает диалоговое окно Модели процесса.
В области Model Transfer Function задайте следующие опции:
- В группе Poles выберите 2 и Underdamped. Этот выбор обновляет Передаточную Функцию Модели на структуру модели второго порядка, которая может содержать сложные полюса. Убедитесь, что флажки Zero и Integrator сняты, чтобы исключить из модели нуль и интегратор (саморегулирующийся).
- Disturbance Model - Установите на Order 1 для оценки модели шума H как модели ARMA первого порядка в непрерывном времени:
  $H = \frac{C}{D} e$
  где и D - полиномы первого порядка, а e - белый шум.
  Это действие задает Focus следующим Prediction, что улучшает точность в частотной области значений, где уровень шума низкий. Для примера, если на высоких частотах больше шума, алгоритм присваивает меньшее значение, чтобы точно подбор кривой высокочастотные фрагменты данных.
- Name - Отредактируйте имя модели, чтобы P2DUe1 чтобы сгенерировать модель с уникальным именем в приложении Системы идентификации.
Нажмите Estimate.
В диалоговом окне Моделей процесса» установите значение Disturbance Model Order 2 для оценки модели шума второго порядка.
Отредактируйте поле Name, чтобы P2DUe2 чтобы сгенерировать модель с уникальным именем в приложении Системы идентификации.
Нажмите Estimate.

Валидация моделей

В этом фрагменте руководства вы оцениваете производительность модели с помощью графиков Выход модели и Остаточный анализ.

Вы должны были уже оценить модели, как описано в Оценке передаточной функции второго порядка с использованием настроек по умолчанию и Оценке модели процесса второго порядка со сложными полюсами.

Если вы не выполнили эти шаги, щелкните здесь, чтобы завершить их.

Сравнение выходных графиков модели. Чтобы сгенерировать график Выхода модели, установите флажок Model output в приложении Системы идентификации. Если график пуст или выход модели не отображается на графике, щелкните значки модели в окне приложения Системы идентификации, чтобы отобразить эти модели на графике.

Следующий график Model Выхода показывает по умолчанию выход моделируемой модели. Симулированный отклик моделей примерно одинаковая для моделей с шумом и без него. Таким образом, включение шумовой модели не влияет на моделируемый выход.

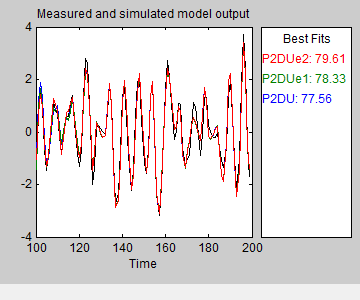
Чтобы просмотреть предсказанные выходы модели, выберите Options > 5 step ahead predicted output в окне Model Выхода графика.

Следующий график Выход показывает, что предсказанный выход модели P2DUe2 (с шумовой моделью второго порядка) лучше предсказанного выхода двух других моделей (без шума и с шумовой моделью первого порядка, соответственно).

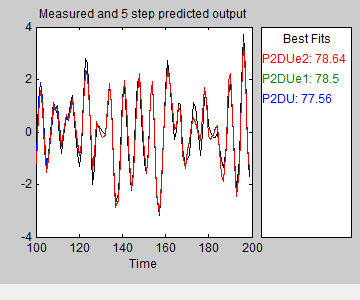
Сравнение Остаточных Графиков для анализа. Чтобы сгенерировать График для анализа Невязки, установите флажок Model resids в приложении Системы идентификации. Если график пуст, щелкните значки модели в окне Системы идентификации приложения, чтобы отобразить эти модели на графике.

P2DUe2 находится в пределах доверительных границ на графике Остаточного анализа.

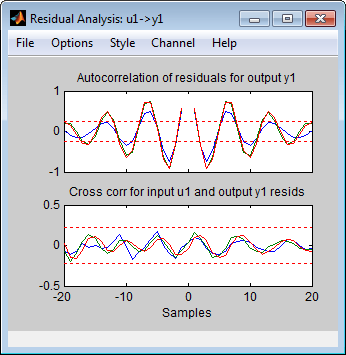
Чтобы просмотреть невязки для P2DUe2 только, удалите модели P2DU и P2DUe1 из Графика для анализа Невязка нажав соответствующие значки в приложении Системы идентификации.

График Остаточного анализа обновляется, как показано на следующем рисунке.

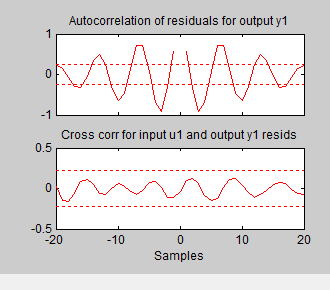
Тест белизны на P2DUe2 показывает, что невязки являются некоррелированными, и тест независимости не показывает корреляции между невязками и входами. Эти тесты указывают, что P2DUe2 является хорошей моделью.

Просмотр параметров модели

Просмотр значений параметров модели

Можно просмотреть числовые значения параметров и другую информацию о модели P2DUe2 щелкните правой кнопкой значок модели в приложении System Identification. Откроется диалоговое окно Data/model Info.

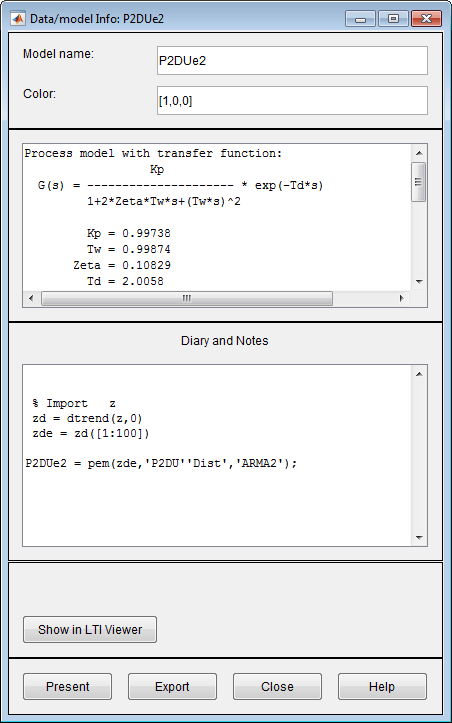
В неотредактируемой области диалогового окна перечислены коэффициенты модели, которые соответствуют следующей структуре модели:

$G (s) = \frac{K}{(1 + 2 ξ T_{w} s + T_{w}^{2} s^{2})} e^{- T_{d} s}$

Коэффициенты согласуются с моделью, используемой для моделирования данных:

$G (s) = \frac{1}{1 + 0.2 s + s^{2}} e^{- 2 s}$

Просмотр неопределенностей параметра

Чтобы просмотреть неопределенности параметров для системной передаточной функции, нажмите Present в диалоговом окне Data/model Info и просмотрите информацию в Командном окне MATLAB.

Kp = 0.99821 +/- 0.019982
Tw = 0.99987 +/- 0.0037697
Zeta = 0.10828 +/- 0.0042304
Td = 2.004 +/- 0.0029717

Неопределенность 1-стандартного отклонения для каждого параметра модели следует +/- символ.

P2DUe2 также включает аддитивный шумовой термин, где H - модель ARMA второго порядка, а e - белый шум:

$H = \frac{C}{D} e$

Программа отображает шумовую модель H как отношение двух полиномов, C(s)/D(s), где:

 C(s) = s^2 + 2.186 (+/- 0.08467) s + 1.089 (+/- 0.07951)
 D(s) = s^2 + 0.2561 (+/- 0.09044) s + 0.5969 (+/- 0.3046)

1-стандартная неопределенность отклонения для параметров модели находится в круглых скобках рядом с каждым значением параметров.

Экспорт модели в рабочее пространство MATLAB

Можно выполнить последующий анализ на оценочных моделях из Рабочего пространства MATLAB. Например, если модель является объектом, которому требуется контроллер, можно импортировать модель из рабочего пространства MATLAB в продукт Control System Toolbox™. Кроме того, чтобы симулировать вашу модель в программном обеспечении Simulink (возможно, как часть большей динамической системы), можно импортировать эту модель как блок Simulink.

Модели, созданные вами в приложении Системы идентификации, не доступны автоматически в рабочем пространстве MATLAB. Чтобы сделать модель доступной для других тулбоксов, Simulink и команд System Identification Toolbox, необходимо экспортировать модель из приложения Системы идентификации в Рабочее пространство MATLAB.

Как экспортировать P2DUe2 перетащите значок модели в прямоугольник To Workspace в Систему идентификации приложении. Кроме того, нажмите Export в диалоговом окне Data/model Info. Теперь модель появится в браузере Рабочего пространства MATLAB.

Примечание

Эта модель является idproc объект модели.

Симуляция модели System Identification Toolbox в программном обеспечении Simulink

Необходимые условия для этого руководства

В этом руководстве вы создаете простую модель Simulink, которая использует блоки из библиотеки System Identification Toolbox, чтобы принести данные z и модель P2DUe2 в Simulink.

Чтобы выполнить шаги, указанные в этом руководстве, Simulink должен быть установлен на вашем компьютере.

Кроме того, вы должны уже выполнить следующие шаги:

Загрузите набор данных, как описано в разделе Загрузка данных в рабочее пространство MATLAB.
Оцените модель процесса второго порядка, как описано в Оценке модели процесса второго порядка со сложными полюсами.
Экспорт модели в рабочее пространство MATLAB, как описано в разделе Экспорт модели в рабочем пространстве MATLAB.

Если вы не выполнили эти шаги, щелкните здесь, чтобы завершить их. Затем перетащите z и P2DUe2 Значки с To Workspace прямоугольником в приложении Системы идентификации. Кроме того, нажмите Export в диалоговом окне Data/model Info. Теперь данные и модель появляются в браузере Рабочее Пространство MATLAB.

Подготовка входных данных

Используйте канал входа набора данных z как вход для симуляции вывода модели путем ввода следующего в Командном окне MATLAB:

z_input = z;    % Creates a new iddata object.
z_input.y = []; % Sets the output channel
               % to empty.

Также можно задать любой входной сигнал.

Подробнее. Для получения дополнительной информации о представлении сигналов данных для идентификации системы смотрите Представление данных в Рабочем пространстве MATLAB.

Создание модели Simulink

Чтобы добавить блоки к модели Simulink:

На вкладке Home MATLAB нажмите Simulink.
На начальной странице Simulink нажмите Blank Model. Затем нажмите Create Model, чтобы открыть новое окно модели.
В окне модели Simulink щелкните, чтобы открыть браузер библиотек. В браузере библиотек выберите библиотеку System Identification Toolbox. В правой части окна отображаются блоки, относящиеся к продукту System Identification Toolbox.
Совет
Кроме того, для доступа к библиотеке Системы идентификации блоков введите slident в Командном Окне MATLAB.
Перетащите следующие блоки System Identification Toolbox в новое окно модели:
- Блок приемника IDDATA
- Исходный блок IDDATA
- Блок модели IDMODEL
В браузере библиотеки Simulink выберите библиотеку Simulink > Sinks и перетащите блок Scope в окно новой модели.
В окне модели Simulink соедините блоки так, чтобы они напоминали следующий рисунок.

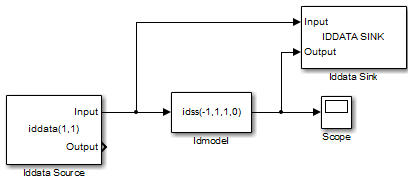
Затем вы конфигурируете эти блоки, чтобы получить данные из рабочего пространства MATLAB и задать временной интервал и длительность симуляции.

Конфигурирование блоков и параметров симуляции

Эта процедура проведет вас через следующие задачи, чтобы сконфигурировать блоки модели:

Получение данных из рабочего пространства MATLAB.
Установка временного интервала и длительности симуляции.

В редакторе Simulink выберите Modeling > Model Settings > Model Settings Ctrl+E.
В диалоговом окне Параметров конфигурации, в подпанели Solver, в поле Stop time, введите 200. Нажмите OK.
Это значение устанавливает длительность симуляции в 200 секунд.
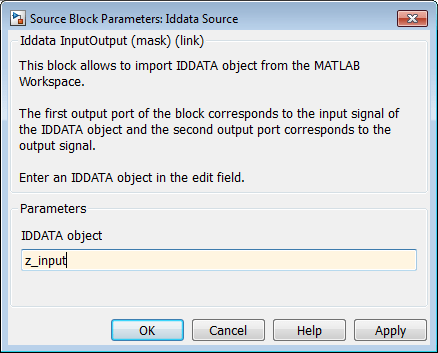
Дважды кликните блок Iddata Source, чтобы открыть диалоговое окно Исходный Блок Parameters: Iddata Source. Затем введите в поле IDDATA object следующее имя переменной:
```
z_input
```
Эта переменная является объектом данных в рабочем пространстве MATLAB, который содержит входные данные.

Совет
В качестве ярлыка можно перетащить имя переменной из браузера Рабочего пространства MATLAB в IDDATA object поле.
Нажмите OK.
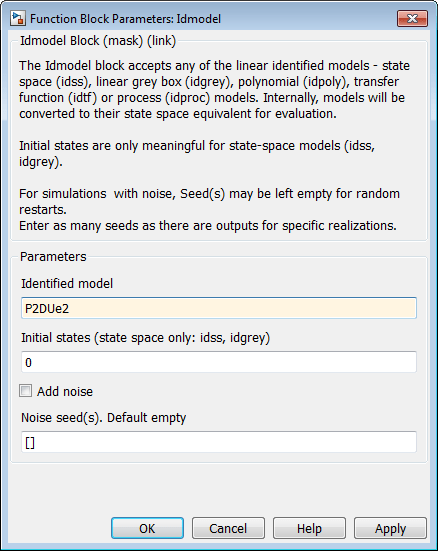
Дважды кликните блок Idmodel, чтобы открыть диалоговое окно Function Block Parameters: Idmodel.
1. Введите в поле Model variable следующее имя переменной:
  P2DUe2
  Эта переменная представляет имя модели в рабочем пространстве MATLAB.
2. Снимите флажок Add noise, чтобы исключить шум из симуляции. Нажмите OK.
  Когда Add noise выбран, Simulink выводит амплитуду шума из NoiseVariance свойство модели и добавляет шум к модели соответственно. Симуляция распространяет этот шум согласно модели шума H, которая была оценена с динамикой системы:
  
  $H = \frac{C}{D} e$
Нажмите OK.
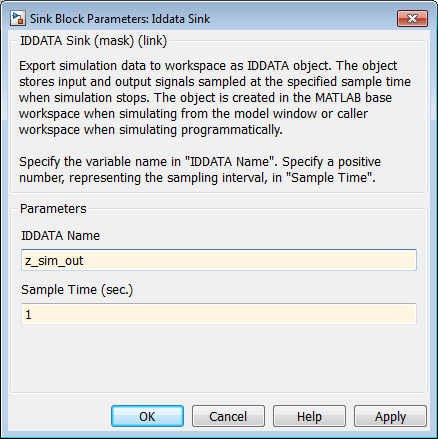
Дважды кликните блок Iddata Sink, чтобы открыть диалоговое окно Sink Block Parameters: Iddata Sink. Введите в поле IDDATA Name следующее имя переменной:
z_sim_out
Тип 1 в поле Sample Time (sec.), чтобы задать шаг расчета выходных данных, чтобы соответствовать шагу расчета входных данных.

Нажмите OK.

Получившееся изменение модели Simulink показано на следующем рисунке.

Выполнение симуляции

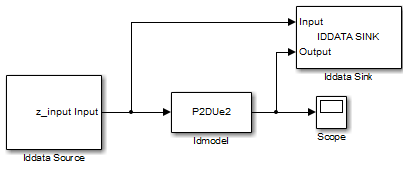
В редакторе Simulink выберите Simulation > Run.
Дважды кликните блок Scope, чтобы отобразить график времени выхода модели.
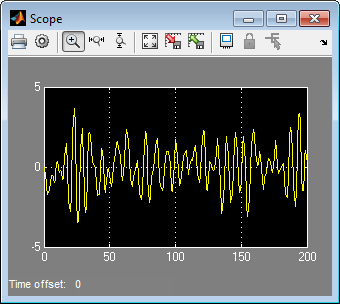
В браузере Рабочего пространства MATLAB заметьте переменную z_sim_out который хранит выходы модели как iddata объект. Это имя переменной задается при конфигурировании блока Iddata Sink.
Эта переменная хранит моделируемый выход модели, и теперь она доступна для дальнейшей обработки и исследования.

Документация