Exponenta Banner

unscentedKalmanFilter

Создайте сигма-точечный фильтр Калмана объект для онлайн-оценки состояния

Свернуть все на странице

Синтаксис

obj = unscentedKalmanFilter(StateTransitionFcn,MeasurementFcn,InitialState)
obj = unscentedKalmanFilter(StateTransitionFcn,MeasurementFcn,InitialState,Name,Value)
obj = unscentedKalmanFilter(StateTransitionFcn,MeasurementFcn)
obj = unscentedKalmanFilter(StateTransitionFcn,MeasurementFcn,Name,Value)
obj = unscentedKalmanFilter(Name,Value)

Описание

пример

obj = unscentedKalmanFilter(StateTransitionFcn,MeasurementFcn,InitialState) создает объект сигма-точечного фильтра Калмана для онлайн-оценки состояния нелинейной системы дискретного времени. StateTransitionFcn - функция, которая вычисляет состояние системы в момент k времени, учитывая вектор состояния в момент времени k -1. MeasurementFcn является функцией, которая вычисляет выходное измерение системы в момент времени k, учитывая состояние в момент k. InitialState задает начальное значение оценок состояния.

После создания объекта используйте correct и predict команды для обновления оценок состояний и ошибки расчета состояний ковариации значений с помощью алгоритма дискретного времени сигма-точечного фильтра Калмана и данных в реальном времени.

пример

obj = unscentedKalmanFilter(StateTransitionFcn,MeasurementFcn,InitialState,Name,Value) задает дополнительные атрибуты объекта сигма-точечного фильтра Калмана с помощью одного или нескольких Name,Value аргументы в виде пар.

obj = unscentedKalmanFilter(StateTransitionFcn,MeasurementFcn) создает объект сигма-точечного фильтра Калмана с помощью заданных функций перехода и измерения. Перед использованием predict и correct команды, задайте начальные значения состояния с помощью записи через точку. Для примера - для системы с двумя состояниями с начальными значениями состояний [1;0], задайте obj.State = [1;0].

obj = unscentedKalmanFilter(StateTransitionFcn,MeasurementFcn,Name,Value) задает дополнительные атрибуты объекта сигма-точечного фильтра Калмана с помощью одного или нескольких Name,Value аргументы в виде пар. Перед использованием predict и correct команды, задайте начальные значения состояния используя Name,Value аргументы в виде пар или запись через точку.

пример

obj = unscentedKalmanFilter(Name,Value) создает объект сигма-точечного фильтра Калмана со свойствами, заданными с помощью одного или нескольких Name,Value аргументы в виде пар. Перед использованием predict и correct команды, задайте функцию перехода состояния, функцию измерения и начальные значения состояния используя Name,Value аргументы в виде пар или запись через точку.

Описание объекта

unscentedKalmanFilter создает объект для онлайн-оценки состояния нелинейной системы дискретного времени с помощью алгоритма сигма-точечного фильтра Калмана дискретного времени.

Рассмотрим объект с x состояниями, входными u, выходными y, технологическими шумовыми w и шумовыми v измерения. Предположим, что можно представлять объект как нелинейную систему.

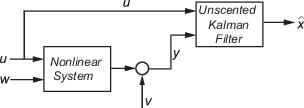
Алгоритм вычисляет оценки состояния x^ нелинейной системы с использованием заданных Вами функций перехода и измерения. Программа позволяет вам задать шум в этих функциях как аддитивный или неаддитивный:

  • Условия аддитивного шума - Переходы состояний и уравнения измерений имеют следующую форму:

    x[k]=f(x[k−1],us[k−1])+w[k−1]y[k]=h(x[k],um[k])+v[k]

    Здесь f является нелинейной функцией перехода состояния, которая описывает эволюцию состояний x от одного временного шага до следующего. Нелинейная функция измерения h связана x к измерениям y в временной шаг k. w и v являются нулевым средним, некоррелированным процессом и измерительными шумами, соответственно. Эти функции могут также иметь дополнительные входные параметры, которые обозначаются us и um в уравнениях. Для примера дополнительные аргументы могут быть временным шагом k или входы u в нелинейную систему. Таких аргументов может быть несколько.

    Обратите внимание, что условия шума в обоих уравнениях аддитивны. То есть x(k) линейно связан с технологическим шумом w(k-1), и y(k) линейно связан с шумом измерения v(k).

  • Неаддитивные Условия Шума - Программное обеспечение также поддерживает более комплексный переход состояния и функции измерения, где x состояния [k] и y измерения [k] являются нелинейными функциями технологического шума и шума измерения, соответственно. Когда члены шума неаддитивны, переход состояния и уравнение измерений имеют следующую форму:

    x[k]=f(x[k−1],w[k−1],us[k−1])y[k]=h(x[k],v[k],um[k])

Когда вы выполняете онлайн-оценку состояния, вы сначала создаете нелинейные f функции перехода состояния и h функции измерения. Затем вы создаете unscentedKalmanFilter объект, использующий эти нелинейные функции, и определить, являются ли условия шума аддитивными или неаддитивными. После того, как вы создали объект, вы используете predict команда для предсказания оценок состояния на следующем временном шаге, и correct исправить оценки состояния с помощью алгоритма сигма-точечного фильтра Калмана и данных в реальном времени. Для получения информации об алгоритме см. «Расширенные и нераскрытые алгоритмы фильтра Калмана для оценки состояния в режиме онлайн».

Можно использовать следующие команды с unscentedKalmanFilter объекты:

КомандаОписание
correct

Исправьте состояние и ошибку расчета ковариации во время шага k используя измеренные данные в момент шага k.

predict

Предсказать состояние и ковариацию ошибки расчета состояния в момент следующего временного шага.

residualВерните различие между фактическими и предсказанными измерениями.
clone

Создайте другой объект с теми же значениями свойств объекта.

Не создавать дополнительные объекты с помощью синтаксиса obj2 = obj. Любые изменения, внесенные в свойства нового объекта, созданные таким образом (obj2) также измените свойства исходного объекта (obj).

Для unscentedKalmanFilter свойства объекта, см. Свойства.

Примеры

свернуть все

Открыть Live Script

Чтобы задать объект сигма-точечного фильтра Калмана для оценки состояний вашей системы, вы записываете и сохраняете функцию перехода состояния и функцию измерения для системы.

В этом примере используйте ранее записанные и сохраненные функции перехода и измерения, vdpStateFcn.m и vdpMeasurementFcn.m. Эти функции описывают дискретное приближение к осциллятору Ван дер Поля с параметром нелинейности, mu, равным 1. Генератор имеет два состояния.

Задайте начальное предположение для двух состояний. Вы задаете начальное предположение о состоянии как M- элемент строку или вектор-столбец, где M количество состояний.

initialStateGuess = [1;0];

Создайте объект сигма-точечного фильтра Калмана. Используйте указатели на функцию, чтобы предоставить объекту переходные и измерительные функции.

obj = unscentedKalmanFilter(@vdpStateFcn,@vdpMeasurementFcn,initialStateGuess);

Объект имеет структуру по умолчанию, где шум процесса и измерения являются аддитивными.

Чтобы оценить состояния и ковариацию ошибки расчета состояния от построенного объекта, используйте correct и predict команды и данные в реальном времени.

Открыть Live Script

Создайте сигма-точечный фильтр Калмана для осциллятора Ван дер Поля с двумя состояниями и одним выходом. Используйте ранее написанные и сохраненные функции перехода и измерения, vdpStateFcn.m и vdpMeasurementFcn.m. Эти функции записаны для аддитивного процесса и терминов шума измерения. Задайте начальные значения для двух состояний как [2; 0].

Поскольку система имеет два состояния, а шум процесса является аддитивным, шум процесса является 2-элементным вектором, а ковариация шума процесса является матрицей 2 на 2. Предположим, что нет перекрестной корреляции между терминами шума процесса, и оба члена имеют одинаковое отклонение 0,01. Можно задать ковариацию шума процесса как скаляр. Программа использует скалярное значение, чтобы создать диагональную матрицу 2 на 2 с 0,01 на диагоналях.

Задайте ковариацию технологического шума во время конструкции объекта.

obj = unscentedKalmanFilter(@vdpStateFcn,@vdpMeasurementFcn,[2;0],...
    'ProcessNoise',0.01);

Также можно задать шумовые ковариации после конструкции объекта с помощью записи через точку. Для примера задайте ковариацию шума измерения как 0,2.

obj.MeasurementNoise = 0.2;

Поскольку система имеет только один выход, шум измерения является вектором с 1 элементом и MeasurementNoise свойство обозначает отклонение шума измерения.

Открыть Live Script

Создайте сигма-точечный фильтр Калмана для осциллятора Ван дер Поля с двумя состояниями и одним выходом. Примите, что условия технологического шума в функции перехода состояния аддитивны. То есть существует линейное соотношение между состоянием и технологическим шумом. Также примите, что члены шума измерения являются неаддитивными. То есть существует нелинейное отношение между шумом измерения и шумом измерения.

obj = unscentedKalmanFilter('HasAdditiveMeasurementNoise',false);

Задайте функцию перехода состояния и функции измерения. Используйте ранее написанные и сохраненные функции, vdpStateFcn.m и vdpMeasurementNonAdditiveNoiseFcn.m.

Функция перехода состояния записывается, принимая, что технологический шум является аддитивным. Функция измерения записывается, принимая, что шум измерения неаддитивен. 

obj.StateTransitionFcn = @vdpStateFcn;
obj.MeasurementFcn = @vdpMeasurementNonAdditiveNoiseFcn;

Задайте начальные значения для двух состояний как [2; 0].

obj.State = [2;0];

Теперь можно использовать correct и predict команды для оценки состояния и ошибки расчета состояния ковариации значений от построенного объекта.

Открыть Live Script

Рассмотрим нелинейную систему с входными u чье состояние x и измерительные y развиваться согласно следующим переходным и измерительным уравнениям:

x[k]=x[k-1]+u[k-1]+w[k-1]

y[k]=x[k]+2*u[k]+v[k]2

Шум процесса w системы является аддитивным, в то время как шум измерения v является неаддитивным.

Создайте функцию перехода состояния и функцию измерения для системы. Задайте функции с дополнительным входом u.

f = @(x,u)(sqrt(x+u));
h = @(x,v,u)(x+2*u+v^2);

f и h являются указателями на функцию анонимных функций, которые хранят функции перехода и измерения состояния, соответственно. В функции измерения, потому что шум измерения неаддитивен, v задается также как вход. Обратите внимание, что v задается как вход перед дополнительным входом u.

Создайте объект сигма-точечного фильтра Калмана для оценки состояния нелинейной системы с помощью заданных функций. Задайте начальное значение состояния как 1, и шум измерения как неаддитивный.

obj = unscentedKalmanFilter(f,h,1,'HasAdditiveMeasurementNoise',false);

Задайте ковариацию шума измерения.

obj.MeasurementNoise = 0.01;

Теперь можно оценить состояние системы с помощью predict и correct команды. Вы передаете значения u на predict и correct, которые в свою очередь передают их в функции переходов состояний и измерений, соответственно.

Исправьте оценку состояния с измерением y [k] = 0,8 и входом u [k] = 0,2 на временном шаге k.

correct(obj,0.8,0.2)

Предсказать состояние на следующем временном шаге, заданном u [k] = 0,2.

predict(obj,0.2)

Входные параметры

свернуть все

Переходная функция f состояния, заданная как указатель на функцию. Функция вычисляет вектор состояния Ns-element системы на временной шаг k, учитывая вектор состояния на временной шаг k-1. Ns - количество состояний нелинейной системы.

Вы записываете и сохраняете функцию перехода состояния для вашей нелинейной системы и используете ее, чтобы создать объект. Для примера, если vdpStateFcn.m является функцией перехода к состоянию, задайте StateTransitionFcn как @vdpStateFcn. Можно также задать StateTransitionFcn как указатель на функцию для анонимной функции.

Входы функции, которую вы записываете, зависят от того, задаете ли вы шум процесса как аддитивный или неаддитивный в HasAdditiveProcessNoise свойство объекта:

  • HasAdditiveProcessNoise is true - шум процесса w является аддитивным, и функция перехода состояния задает, как состояния развиваются как функция от значений состояния на предыдущем временном шаге:

    x(k) = f(x(k-1),Us1,...,Usn)

    Где x(k) - расчетное состояние во времени k, и Us1,...,Usn - любые дополнительные входные аргументы, требуемые функцией перехода вашего состояния, такие как входы или шаг расчета. Во время оценки вы передаете эти дополнительные аргументы в predict команда, которая в свою очередь передает их в функцию перехода состояния.

  • HasAdditiveProcessNoise является ложным - шум процесса является неаддитивным, и функция перехода состояния также задает, как состояния развиваются как функция шума процесса:

    x(k) = f(x(k-1),w(k-1),Us1,...,Usn)

Чтобы увидеть пример функции перехода состояния с аддитивным технологическим шумом, введите edit vdpStateFcn в командной строке.

Функция h измерения, заданная как указатель на функцию. Функция вычисляет выходной вектор измерения N-элемента нелинейной системы на временном шаге k, учитывая вектор состояния на временном шаге k. N - количество измерений системы. Вы записываете и сохраняете функцию измерения и используете ее для создания объекта. Для примера, если vdpMeasurementFcn.m является функцией измерения, задайте MeasurementFcn как @vdpMeasurementFcn. Можно также задать MeasurementFcn как указатель на функцию для анонимной функции.

Входы функции зависят от того, задаете ли вы шум измерения как аддитивный или неаддитивный в HasAdditiveMeasurementNoise свойство объекта:

  • HasAdditiveMeasurementNoise is true - Измерительный шум v является аддитивным, и функция измерения определяет, как измерения развиваются как функция от значений состояния:

    y(k) = h(x(k),Um1,...,Umn)

    Где y(k) и x(k) - это расчетный выход и расчетное состояние во времени k, и Um1,...,Umn все необязательные входные параметры, требуемые вашей функцией измерения. Для примера, если вы используете несколько датчиков для отслеживания объекта, дополнительным входом может стать положение датчика. Во время оценки вы передаете эти дополнительные аргументы в correct команда, которая в свою очередь передает их в функцию измерения.

  • HasAdditiveMeasurementNoise является ложным - шум измерения является неаддитивным, и функция измерения также определяет, как формируется выходное измерение как функция шума измерения:

    y(k) = h(x(k),v(k),Um1,...,Umn)

Чтобы увидеть пример функции измерения с аддитивным технологическим шумом, введите edit vdpMeasurementFcn в командной строке. Чтобы увидеть пример функции измерения с неаддитивным шумом процесса, введите edit vdpMeasurementNonAdditiveNoiseFcn.

Начальные оценки состояния, заданные как Ns вектор -элемент, где Ns - количество состояний в системе. Задайте начальные значения состояния на основе ваших знаний о системе.

Заданное значение сохранено в State свойство объекта. Если вы задаете InitialState в качестве вектора-столбца затем State также является вектор-столбец, и predict и correct команды возврата оценки состояния в виде вектора-столбца. В противном случае возвращается вектор-строка.

Если вам нужен фильтр с переменными с одной точностью с плавающей точкой, задайте InitialState как переменный вектор с одной точностью. Для примера - для двухгосударственной системы с переходом состояний и функциями измерения vdpStateFcn.m и vdpMeasurementFcn.m, создайте объект сигма-точечного фильтра Калмана с начальными состояниями [1;2] следующим образом:

obj = unscentedKalmanFilter(@vdpStateFcn,@vdpMeasurementFcn,single([1;2]))

Типы данных: double | single

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

Использование Name,Value аргументы для задания свойств unscentedKalmanFilter объект во время создания объекта. Для примера создать объект сигма-точечного фильтра Калмана и задать ковариацию шума процесса равной 0,01:

obj = unscentedKalmanFilter(StateTransitionFcn,MeasurementFcn,InitialState,'ProcessNoise',0.01);

Свойства

свернуть все

unscentedKalmanFilter свойства объекта имеют три типа:

  • Настраиваемые свойства, которые можно задать несколько раз, или во время конструкции объекта с помощью Name,Value аргументы или любое время после во время оценки состояния. После создания объекта используйте запись через точку для изменения настраиваемых свойств.

    obj = unscentedKalmanFilter(StateTransitionFcn,MeasurementFcn,InitialState);
obj.ProcessNoise = 0.01;

    Настраиваемые свойства State, StateCovariance, ProcessNoise, MeasurementNoise, Alpha, Beta, и Kappa.

  • Нетронутые свойства, которые можно задать один раз, либо во время конструкции объекта, либо после с помощью понятия точки. Задайте эти свойства перед оценкой состояния используя correct и predict. The StateTransitionFcn и MeasurementFcn свойства относятся к этой категории.

  • Нетронутые свойства, которые необходимо задать во время конструкции объекта. The HasAdditiveProcessNoise и HasAdditiveMeasurementNoise свойства относятся к этой категории.

Разброс точек сигмы вокруг среднего значения состояния, заданный как скалярное значение между 0 и 1 (0 <Alpha <= 1).

Сигма-точечный фильтр Калмана рассматривает состояние системы как случайную переменную со средним значением State и дисперсионные StateCovariance. Чтобы вычислить состояние и его статистические свойства на следующем временном шаге, алгоритм сначала генерирует набор значений состояния, распределенных вокруг среднего State значение при помощи нескромного преобразования. Эти значения сгенерированного состояния называются точки. Алгоритм использует каждую из точек сигмы как вход в функции перехода и измерения состояния, чтобы получить новый набор преобразованных точек состояния и измерений. Преобразованные точки используются, чтобы вычислить состояние и ковариационное значение ошибки расчета состояния на следующем временном шаге.

Разброс точек сигмы вокруг среднего значения состояния управляется двумя параметрами Alpha и Kappa. Третий параметр, Beta, влияет на веса преобразованных точек во время вычислений состояния и ковариации измерений:

  • Alpha - Определяет разброс точек сигмы вокруг среднего значения состояния. Обычно это небольшое положительное значение. Разброс точек сигмы пропорционален Alpha. Меньшие значения соответствуют точкам сигмы ближе к среднему состоянию.

  • Kappa - Второй параметр масштабирования, который обычно устанавливается на 0. Меньшие значения соответствуют точкам сигмы ближе к среднему состоянию. Спред пропорционален квадратному корню Kappa.

  • Beta - Включает в себя предварительные знания о распределении состояния. Для Гауссовых распределений, Beta = 2 оптимально.

Если вы знаете распределение ковариации состояний и состояний, можно настроить эти параметры, чтобы захватить преобразование моментов более высокого порядка распределения. Алгоритм может отслеживать только один пик в распределение вероятностей состояния. Если в распределении состояний вашей системы есть несколько пиков, можно настроить эти параметры так, чтобы точки сигмы оставались около одного пика. Например, выберите небольшую Alpha чтобы сгенерировать сигму точек близкую к среднему значению состояния.

Для получения дополнительной информации см. Сигма-точечный фильтр Калмана алгоритма.

Alpha является настраиваемым свойством. Изменить его можно с помощью записи через точку.

Характеристика распределения состояний, которая используется для регулировки весов преобразованных точек сигмы, заданная как скалярное значение, больше или равное 0. Для Гауссовых распределений, Beta = 2 является оптимальным выбором.

Для получения дополнительной информации смотрите Alpha описание свойства.

Beta является настраиваемым свойством. Изменить его можно с помощью записи через точку.

Характеристики шума измерения, заданные как одно из следующих значений:

  • true - Измерительный шум v является аддитивной. Функция измерения h которая задана в MeasurementFcn имеет следующую форму:

    y(k) = h(x(k),Um1,...,Umn)

    Где y(k) и x(k) - это расчетный выход и расчетное состояние во времени k, и Um1,...,Umn все необязательные входные параметры, требуемые вашей функцией измерения.

  • false - Шум измерения неаддитивен. Функция измерения задает, как выходное измерение развивается как функция состояния и шума измерения:

    y(k) = h(x(k),v(k),Um1,...,Umn)

HasAdditiveMeasurementNoise является свойством nontunable, и его можно задать только во время конструкции объекта. Вы не можете изменить его с помощью записи через точку.

Характеристики технологического шума, заданные как одно из следующих значений:

  • true - Технологический шум w является аддитивной. Функция перехода f заданная в StateTransitionFcn имеет следующую форму:

    x(k) = f(x(k-1),Us1,...,Usn)

    Где x(k) - расчетное состояние во времени k, и Us1,...,Usn - любые дополнительные входные параметры, требуемые функцией перехода состояния.

  • false - Технологический шум неаддитивен. Функция перехода состояния задает, как состояния развиваются как функция состояния и обрабатывают шум на предыдущем временном шаге:

    x(k) = f(x(k-1),w(k-1),Us1,...,Usn)

HasAdditiveProcessNoise является свойством nontunable, и его можно задать только во время конструкции объекта. Вы не можете изменить его с помощью записи через точку.

Разброс точек сигмы вокруг среднего значения состояния, заданный как скалярное значение между 0 и 3 (0 <= Kappa <= 3). Kappa обычно задается как 0. Меньшие значения соответствуют точкам сигмы ближе к среднему состоянию. Спред пропорционален квадратному корню Kappa. Для получения дополнительной информации смотрите Alpha описание свойства.

Kappa является настраиваемым свойством. Изменить его можно с помощью записи через точку.

Функция h измерения, заданная как указатель на функцию. Функция вычисляет выходной вектор измерения N-элемента нелинейной системы на временном шаге k, учитывая вектор состояния на временном шаге k. N - количество измерений системы. Вы записываете и сохраняете функцию измерения и используете ее, чтобы создать объект. Для примера, если vdpMeasurementFcn.m является функцией измерения, задайте MeasurementFcn как @vdpMeasurementFcn. Можно также задать MeasurementFcn как указатель на функцию для анонимной функции.

Входы функции зависят от того, задаете ли вы шум измерения как аддитивный или неаддитивный в HasAdditiveMeasurementNoise свойство объекта:

  • HasAdditiveMeasurementNoise is true - Измерительный шум v является аддитивным, и функция измерения определяет, как измерения развиваются как функция от значений состояния:

    y(k) = h(x(k),Um1,...,Umn)

    Где y(k) и x(k) - это расчетный выход и расчетное состояние во времени k, и Um1,...,Umn все необязательные входные параметры, требуемые вашей функцией измерения. Для примера, если вы используете несколько датчиков для отслеживания объекта, дополнительным входом может стать положение датчика. Во время оценки вы передаете эти дополнительные аргументы в correct команда, которая в свою очередь передает их в функцию измерения.

  • HasAdditiveMeasurementNoise является ложным - шум измерения является неаддитивным, и функция измерения также определяет, как формируется выходное измерение как функция шума измерения:

    y(k) = h(x(k),v(k),Um1,...,Umn)

Чтобы увидеть пример функции измерения с аддитивным технологическим шумом, введите edit vdpMeasurementFcn в командной строке. Чтобы увидеть пример функции измерения с неаддитивным шумом процесса, введите edit vdpMeasurementNonAdditiveNoiseFcn.

MeasurementFcn является свойством nontunable. Вы можете задать его один раз, прежде чем использовать correct команда либо во время конструкции объекта, либо с использованием записи через точку после конструкции объекта. Вы не можете изменить его после использования correct команда.

Ковариация шума измерения, заданная как скаляр или матрица в зависимости от значения HasAdditiveMeasurementNoise свойство:

  • HasAdditiveMeasurementNoise is true - Задайте ковариацию как скаляр или N матрицу -by N, где N - количество измерений системы. Задайте скаляр, если нет перекрестной корреляции между терминами шума измерения и все члены имеют одинаковое отклонение. Программа использует скалярное значение, чтобы создать N -by N диагональную матрицу.

  • HasAdditiveMeasurementNoise is false - Задайте ковариацию как V -by - V матрицу, где V - количество членов шума измерения. MeasurementNoise должен быть задан перед использованием correct. После того, как вы задаете MeasurementNoise как матрица впервые, чтобы затем изменить MeasurementNoise можно также задать его как скаляр. Задайте как скаляр, если нет перекрестной корреляции между терминами шума измерения и все члены имеют одинаковое отклонение. Программа расширяет скаляр до V -by V диагональной матрицы со скаляром на диагоналях.

MeasurementNoise является настраиваемым свойством. Изменить его можно с помощью записи через точку.

Ковариация шума процесса, заданная как скаляр или матрица в зависимости от значения HasAdditiveProcessNoise свойство:

  • HasAdditiveProcessNoise is true - Задайте ковариацию как скаляр или Ns матрицу -by Ns, где Ns - количество состояний системы. Задайте скаляр, если нет перекрестной корреляции между терминами шума процесса, и все члены имеют одинаковое отклонение. Программа использует скалярное значение, чтобы создать Ns -by Ns диагональную матрицу.

  • HasAdditiveProcessNoise is false - Задайте ковариацию как W -by - W матрицу, где W - количество членов шума процесса. ProcessNoise должен быть задан перед использованием predict. После того, как вы задаете ProcessNoise как матрица впервые, чтобы затем изменить ProcessNoise можно также задать его как скаляр. Задайте как скаляр, если нет перекрестной корреляции между терминами шума процесса и все члены имеют одинаковое отклонение. Программа расширяет скаляр до W -by W диагональной матрицы.

ProcessNoise является настраиваемым свойством. Изменить его можно с помощью записи через точку.

Состояние нелинейной системы, заданное как вектор размера Ns, где Ns - количество состояний системы.

Когда вы используете predict команда, State обновляется предсказанным значением на временном шаге k используя значение состояния на временном шаге k -1. Когда вы используете correct команда, State обновляют оценочным значением на временной шаг k используя измеренные данные на временной шаг k.

Начальное значение State - значение, заданное в InitialState входной параметр во время создания объекта. Если вы задаете InitialState как вектор-столбец, затем State также является вектор-столбец, и predict и correct команды возврата оценки состояния в виде вектора-столбца. В противном случае возвращается вектор-строка. Если вы хотите фильтр с переменными с одной точностью с плавающей точкой, вы должны задать State как переменная с одной точностью во время конструкции объекта с использованием InitialState входной параметр.

State является настраиваемым свойством. Изменить его можно с помощью записи через точку.

Ковариация ошибки расчета состояния, заданная как скаляр или Ns -by - Ns матрица, где Ns - количество состояний системы. Если вы задаете скаляр, программа использует скалярное значение, чтобы создать Ns -by Ns диагональную матрицу.

Задайте высокое значение для ковариации, когда у вас нет доверия в начальных значениях состояния, которые вы задаете в InitialState входной параметр.

Когда вы используете predict команда, StateCovariance обновляется предсказанным значением на временном шаге k используя значение состояния на временном шаге k -1. Когда вы используете correct команда, StateCovariance обновляют оценочным значением на временной шаг k используя измеренные данные на временной шаг k.

StateCovariance является настраиваемым свойством. Вы можете изменить его с помощью записи через точку после использования correct или predict команды.

Переходная функция f состояния, заданная как указатель на функцию. Функция вычисляет вектор состояния Ns-element системы на временной шаг k, учитывая вектор состояния на временной шаг k-1. Ns - количество состояний нелинейной системы.

Вы записываете и сохраняете функцию перехода состояния для вашей нелинейной системы и используете ее, чтобы создать объект. Для примера, если vdpStateFcn.m является функцией перехода к состоянию, задайте StateTransitionFcn как @vdpStateFcn. Можно также задать StateTransitionFcn как указатель на функцию для анонимной функции.

Входы функции, которую вы записываете, зависят от того, задаете ли вы шум процесса как аддитивный или неаддитивный в HasAdditiveProcessNoise свойство объекта:

  • HasAdditiveProcessNoise is true - шум процесса w является аддитивным, и функция перехода состояния задает, как состояния развиваются как функция от значений состояния на предыдущем временном шаге:

    x(k) = f(x(k-1),Us1,...,Usn)

    Где x(k) - расчетное состояние во времени k, и Us1,...,Usn - любые дополнительные входные аргументы, требуемые функцией перехода вашего состояния, такие как входы или шаг расчета. Во время оценки вы передаете эти дополнительные аргументы в predict команда, которая в свою очередь передает их в функцию перехода состояния.

  • HasAdditiveProcessNoise является ложным - шум процесса является неаддитивным, и функция перехода состояния также задает, как состояния развиваются как функция шума процесса:

    x(k) = f(x(k-1),w(k-1),Us1,...,Usn)

Чтобы увидеть пример функции перехода состояния с аддитивным технологическим шумом, введите edit vdpStateFcn в командной строке.

StateTransitionFcn является свойством nontunable. Вы можете задать его один раз, прежде чем использовать predict команда либо во время конструкции объекта, либо с использованием записи через точку после конструкции объекта. Вы не можете изменить его после использования predict команда.

Выходные аргументы

свернуть все

Сигма-точечный фильтр Калмана для онлайн-оценки состояния, возвращенный как unscentedKalmanFilter объект. Этот объект создается с использованием заданных свойств. Используйте correct и predict команды для оценки состояния и ошибки расчета состояния ковариации с помощью алгоритма сигма-точечного фильтра Калмана.

Когда вы используете predict, obj.State и obj.StateCovariance обновляются предсказанным значением на временном шаге k используя значение состояния на временном шаге k -1. Когда вы используетеcorrect, obj.State и obj.StateCovariance обновляют оцененными значениями на временной шаг k используя измеренные данные на временной шаг k.

Вопросы совместимости

расширить все

Поведение изменено в R2020b

Расширенные возможности

.

См. также

Функции

Блоки

Темы

Внешние веб-сайты

Введенный в R2016b

Документация по System Identification Toolbox

Поддержка