Триангуляции часто используются, чтобы представлять 2-D и 3-D геометрические области в таких областях применения, как компьютерная графика, физическое моделирование, географические информационные системы, медицинская визуализация и многое другое. Карта многоугольника показана здесь
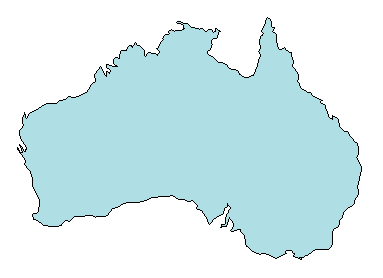
может быть представлено триангуляцией на карте, показанной ниже.
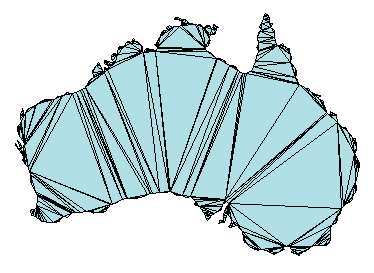
Триангуляция разлагает комплексный полигон на набор более простых треугольных многоугольников. Можно использовать эти многоугольники для разработки основанных на геометрии алгоритмов или графических приложений.
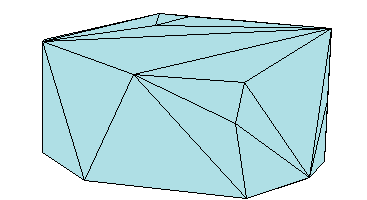
Точно так же можно представлять контур 3-D геометрической области с помощью триангуляции. Рисунок ниже показывает выпуклую оболочку набора точек в трехмерном пространстве. Каждая грань корпуса является треугольником.
MATLAB® использует матричный формат, чтобы представлять триангуляции. Этот формат имеет две части:
Вершины, представленные как матрица, в которой каждая строка содержит координаты точки в триангуляции.
Связность триангуляции, представленная как матрица, в которой каждая строка задает треугольник или тетраэдр.
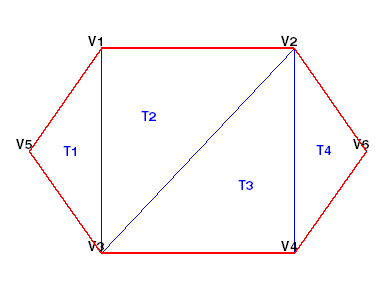
Этот рисунок показывает простую 2-D триангуляцию.
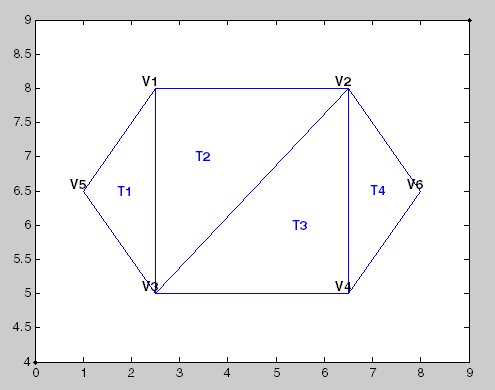
В следующей таблице показана информация о вершине.
| Вершины | ||
|---|---|---|
| Идентификатор вершины | x -координат | y -координат |
| V1 | 2.5 | 8.0 |
| V2 | 6.5 | 8.0 |
| V3 | 2.5 | 5.0 |
| V4 | 6.5 | 5.0 |
| V5 | 1.0 | 6.5 |
| V6 | 8.0 | 6.5 |
Данные в предыдущей таблице хранятся как матрица в среде MATLAB. Идентификаторы вершин являются метками, используемыми для идентификации определенных вершин. Они показаны для иллюстрации концепции идентификатора вершины, но не хранятся явным образом. Вместо этого номера строк матрицы служат идентификаторами вершин.
Данные о связности триангуляции показаны в этой таблице.
| Возможность соединения | |||
|---|---|---|---|
| Идентификатор треугольника | Идентификаторы ограничивающих вершин | ||
| T1 | 5 | 3 | 1 |
| T2 | 3 | 2 | 1 |
| T3 | 3 | 4 | 2 |
| T4 | 4 | 6 | 2 |
Данные в этой таблице хранятся как матрица в среде MATLAB. Идентификаторы треугольников являются метками, используемыми для идентификации определенных треугольников. Они показаны, чтобы проиллюстрировать концепцию идентификатора треугольника, но они не хранятся явным образом. Вместо этого номера строк матрицы служат идентификаторами треугольников.
Можно увидеть этот треугольник T1 задается тремя вершинами, {V5, V3, V1}. Точно так же T4 определяется вершинами, {V4, V6, V2}. Этот формат простирается естественно до более высоких размерностей, которые требуют дополнительных столбцов данных. Для примера тетраэдр в трехмерное пространство определяется четырьмя вершинами, каждая из которых имеет три координаты (x, y, z).
Можно представлять и запрашивать следующие типы триангуляций с помощью MATLAB:
2-D треугольники, состоящие из треугольников, ограниченных вершинами и ребрами
3-D поверхности, состоящие из треугольников, ограниченных вершинами и ребрами
3-D треугольники, состоящие из тетраэдров, ограниченных вершинами, ребрами и гранями
Матричный формат обеспечивает компактное низкоуровневое основанное на массиве представление для триангуляций. Когда вы используете триангуляции для разработки алгоритмов, вам может потребоваться дополнительная информация о геометрических свойствах, топологии и информации о смежности.
Для примера можно вычислить центры вписанной окружности треугольника перед построением аннотированной триангуляции, показанной ниже. В этом случае для отображения меток треугольника (T1, T2 и т.д.) в каждом треугольнике используются центры вписанной окружности наклона. Если необходимо построить график контура красным цветом, необходимо определить ребра, на которые ссылается только один треугольник.
Можно использовать triangulation чтобы создать представление в памяти любых 2-D или 3-D данных триангуляции в матричном формате, таких как матрица, выводимая из delaunay функция или другие программные инструменты. Когда ваши данные представлены с помощью triangulationможно выполнить топологические и геометрические запросы, которые можно использовать для разработки геометрических алгоритмов. Например, можно найти треугольники или тетраэдры, присоединенные к вершине, те, которые имеют одно ребро, их центры описанной окружности и другие функции.
Можно создать triangulation одним из двух способов:
Передайте существующие данные, которые у вас есть в матричном формате, в triangulation. Эти данные могут быть выведены из функции MATLAB, такой как delaunay или convhull. Можно также импортировать данные триангуляции, которые были созданы другим программным обеспечением. Когда вы работаете с импортированными данными, убедитесь, что данные о связности ссылаются на вершинный массив с помощью индексации на основе 1 вместо индексации на основе 0.
Передайте набор точек, чтобы delaunayTriangulation. Получившаяся триангуляция Делоне является особым видом triangulation. Это означает, что вы можете выполнить любое triangulation запрос данных, а также любой специфичный для Delaunay запрос. В более формальных языковых терминах MATLAB, delaunayTriangulation является подклассом triangulation.
Создание триангуляции из матричных данных
В этом примере показано, как использовать данные матрицы триангуляции для создания триангуляции, изучения ее содержания и изучения того, что она может сделать.
Создайте матрицу, P, который содержит данные вершины.
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];Определите связь, T.
T = [5 3 1;
3 2 1;
3 4 2;
4 6 2];Создайте triangulation из этих данных.
TR = triangulation(T,P)
TR =
triangulation with properties:
Points: [6x2 double]
ConnectivityList: [4x3 double]
Доступ к свойствам в triangulation таким же образом вы получаете доступ к полям struct. Например, исследуйте Points свойство, которое содержит координаты вершин.
TR.Points
ans = 6×2
2.5000 8.0000
6.5000 8.0000
2.5000 5.0000
6.5000 5.0000
1.0000 6.5000
8.0000 6.5000
Затем рассмотрим возможность подключения.
TR.ConnectivityList
ans = 4×3
5 3 1
3 2 1
3 4 2
4 6 2
The Points и ConnectivityList свойства определяют матричные данные для триангуляции.
The triangulation класс является оболочкой вокруг матричных данных. Реальная польза - полезность triangulation методы классов. Методы аналогичны функциям, которые принимают triangulation и другие соответствующие входные данные.
The triangulation класс обеспечивает простой способ индексации в ConnectivityList матрица свойств. Доступ к первому треугольнику в триангуляции.
TR.ConnectivityList(1,:)
ans = 1×3
5 3 1
Другой способ получить первый треугольник TR(1,:).
Исследуйте первую вершину первого треугольника.
TR(1,1)
ans = 5
Исследуйте вторую вершину первого треугольника.
TR(1,2)
ans = 3
Теперь рассмотрим все треугольники в триангуляции.
TR(:,:)
ans = 4×3
5 3 1
3 2 1
3 4 2
4 6 2
Использование triplot для построения графика triangulation. The triplot функция не является triangulation метод, но он принимает и может построить triangulation.
figure
triplot(TR)
axis equal
Используйте triangulation метод, freeBoundary, чтобы запросить свободный контур и выделить ее на графике. Этот метод возвращает ребра триангуляции, которые разделяются только одним треугольником. Возвращенные ребра выражены в терминах идентификаторов вершин.
boundaryedges = freeBoundary(TR)';
Теперь постройте график граничных ребер как красной линии.
hold on plot(P(boundaryedges,1),P(boundaryedges,2),'-r','LineWidth',2) hold off

Можно использовать freeBoundary метод для проверки триангуляции. Например, если бы вы наблюдали красные ребра во внутренней части триангуляции, то это указывало бы на проблему в том, как соединяются треугольники.
Создание триангуляции с использованием delaunayTriangulation
В этом примере показано, как создать триангуляцию Делоне с помощью delaunayTriangulation.
Когда вы создаете триангуляцию Делоне с помощью delaunayTriangulation класс, вы автоматически получаете доступ к triangulation методы, потому что delaunayTriangulation является подклассом triangulation.
Создайте delaunayTriangulation из набора точек.
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];
DT = delaunayTriangulation(P)DT =
delaunayTriangulation with properties:
Points: [6x2 double]
ConnectivityList: [4x3 double]
Constraints: []
Результат delaunayTriangulation объект имеет свойства, Points и ConnectivityList, просто как triangulation объект.
Вы можете получить доступ к триангуляции с помощью прямого индексирования, так же как triangulation. Например, исследуйте связность первого треугольника.
DT(1,:)
ans = 1×3
5 3 1
Затем рассмотрим связность всей триангуляции.
DT(:,:)
ans = 4×3
5 3 1
3 4 1
1 4 2
4 6 2
Используйте triplot функция для построения графика триангуляции.
triplot(DT)
axis equal
Родительский класс, triangulation, обеспечивает incenter метод для вычисления центры вписанной окружности каждого треугольника.
IC = incenter(DT)
IC = 4×2
1.8787 6.5000
3.5000 6.0000
5.5000 7.0000
7.1213 6.5000
Возвращенное значение, IC, - массив координат, представляющий центры вписанной окружности треугольников.
Теперь используйте центры вписанной окружности, чтобы найти положения для размещения меток треугольника на графике.
hold on numtri = size(DT,1); trilabels = arrayfun(@(P) {sprintf('T%d', P)}, (1:numtri)'); Htl = text(IC(:,1),IC(:,2),trilabels,'FontWeight','bold', ... 'HorizontalAlignment','center','Color','blue'); hold off

Вместо создания триангуляции Делоне с помощью delaunayTriangulation, вы могли бы использовать delaunay функция, чтобы создать данные связности триангуляции, а затем передать данные связности в triangulation. Для примера,
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];
T = delaunay(P);
TR = triangulation(T,P);
IC = incenter(TR);Оба подхода действительны в этом примере, но если вы хотите создать триангуляцию Делоне и выполнить на ней запросы, то следует использовать delaunayTriangulation по этим причинам:
The delaunayTriangulation класс предоставляет дополнительные методы, которые полезны для работы с триангуляциями. Для примера можно выполнить поиск по ближайшему соседу и точке в треугольнике.
Он позволяет вам редактировать триангуляцию, чтобы добавить, переместить или удалить точки.
Это позволяет вам создавать ограниченные триангуляции Делоне. Это позволяет вам создать триангуляцию для 2-D области.
delaunay | delaunayTriangulation | freeBoundary | triangulation | triplot