power_lineparam

Вычислите параметры RLC воздушной линии электропередачи из ее характеристик проводника и геометрии башни

Синтаксис

LDATA = power_lineparam('new') LDATA = power_lineparam(LDATA) LDATA = power_lineparam('MYLINEDATA') power_lineparam(LDATA,'BLK') power_lineparam('MYLINEDATA','BLK')

Описание

LDATA = power_lineparam('new') возвращает структурную переменную с параметрами геометрии линий по умолчанию. Можно использовать LDATA как переменная шаблона для конфигурирования новой геометрии линии и вычисления параметров линии RLC.

LDATA представляет собой структуру с полями в этой таблице.

Область	Описание
`comments`	Задайте комментарии пользователя, относящиеся к параметрам линии.
`units`	Единицы модулей параметров линии. Установите значение `metric` для определения диаметра проводника, GMR и диаметра пучка в сантиметрах и положения проводника в метрах. Установите значение `English` для определения диаметра проводника, GMR и диаметра пучка в дюймах и положения проводника в футах. Значение по умолчанию является `metric`.
`frequency`	Частота в герце для оценки параметров линии RLC. Значение по умолчанию является `60`.
`groundResistivity`	Сопротивление грунта, в ом-метрах. Установите значение `0` для определения идеально проводящего грунта.
`Geometry`	Структура, задающая геометрию линий и типы проводников.
`Conductors`	Структура, определяющая характеристики проводников для каждого типа.

Geometry представляет собой структуру с полями в этой таблице.

Область	Описание
`NPhaseBundle`	Количество проводников фазы (одинарные проводники или пучки субпроводников). Значение по умолчанию является `3`.
`NGroundBundle`	Количество заземляющих проводов (одиночных проводников или пучков субпроводников). Значение по умолчанию является `2`.
`PhaseNumber`	`1`-by- `NPhaseBundle` + `NGroundBundle` вектор. Этот параметр представляет число фаз, к которому относятся проводники. Несколько проводников могут иметь одинаковое число фаз. Количество фаз заземления `0`. Значение по умолчанию является `[1 2 3 0 0]`.
`X`	`1`-by- `NPhaseBundle` + `NGroundBundle` вектор. Эта настройка представляет горизонтальное положение проводников в метрах или футах. Расположение нулевого опорного положения произвольно. Для симметричной линии обычно выбирают `X = 0` в центре линии. Значение по умолчанию является `[-12 0 12 -8 8]`.
`Ytower`	`1`-by- `NPhaseBundle` + `NGroundBundle` вектор. Эта настройка представляет вертикальное положение проводников (на башне) относительно земли, в метрах или футах. Значение по умолчанию является `[20 20 20 33 33]`.
`Ymin`	`1`-by- `NPhaseBundle` + `NGroundBundle` вектор. Эта настройка представляет вертикальное положение проводников относительно земли в середине диапазона, в метрах или футах. Значение по умолчанию является `[20 20 20 33 33]`.
`ConductorType`	`1`-by- `NPhaseBundle` + `NGroundBundle` вектор. Этот параметр представляет тип проводника. Числа соответствуют элементам вектора, заданным в `Conductors` структура. Значение по умолчанию является `[1 1 1 2 2]`.

Conductors представляет собой структуру с полями в этой таблице. Длина Conductors структура соответствует количеству типов проводников в параметрах линии:

Область	Описание
`Diameter`	Наружный диаметр проводника, см Значение по умолчанию является `[3.5500 1.2700]`.
`ThickRatio`	Отношение T/D полого проводника. T - толщина проводящего материала, D - наружный диаметр. Этот параметр может варьироваться между `0` и `0.5`. A Значение T/D `0.5` указывает сплошной проводник. Для алюминиевых кабельных армированных проводников (ACSR) можно игнорировать стальной сердечник и рассмотреть полый алюминиевый проводник (типичные коэффициенты T/D находятся между `0.3` и `0.4`). Значение по умолчанию `[0.3700 0.5000]`.
`GMR`	Средний радиус геометрии.
`Xa`	Реактивное сопротивление Xa, в омах/км. Значение по умолчанию является `0`.
`Res`	Сопротивление постоянного тока проводника, в омах/км. Значение по умолчанию является `[0.0430 3.1060]`.
`Mur`	Относительная проницаемость проводника. Значение по умолчанию является `[1 1]`.
`NConductors`	Количество проводников на пучок. Значение по умолчанию является `[4 1]`.
`BundleDiameter`	Диаметр пучка, см или дюймов. Значение по умолчанию является `[65 0]`.
`AngleConductor1`	Угол, в степенях, который определяет положение первого проводника в жгуте относительно горизонтальной линии, параллельной земле. Этот угол определяет ориентацию пучка. Значение по умолчанию является `[45 0]`.
`skinEffect`	Установите значение да, чтобы включить влияние частоты на сопротивление и индуктивность переменного тока проводника (эффект кожи). Если установлено значение no, сопротивление остается постоянным при значении, заданном `Res` поле, и индуктивность поддерживается постоянной при значении, вычисленном в DC, используя `Diameter` поле, и `ThickRatio` поле.

LDATA = power_lineparam(LDATA) вычисляет параметры линии RLC для параметров геометрической линии в LDATA структура. Возвращенная структура содержит как геометрические данные, так и вычисленные параметры линии RLC.

The LDATA структура дополнена полями параметров RLC в этой таблице:

Область	Описание
`R`	Матрица N -by N сопротивления линии, в Ом/км.
`L`	Матрица N -by N индуктивности линии, в Henries/km.
`C`	Емкостная матрица N -by-N линии, в Фарадсе/км.
`R10`	Для трехфазной линии эта настройка представляет сопротивления положительной последовательности и нулевой последовательности в омах/км. Для шестифазной линии (две соединенные трехфазные схемы) эта настройка представляет сопротивления положительной последовательности и нулевой последовательности схемы 1, взаимное сопротивление нулевой последовательности между схемой 1 и схемой 2 и сопротивления положительной последовательности и нулевой последовательности схемы 2.
`L10`	Для трехфазной линии, индуктивности положительной последовательности и нулевой последовательности, в Henries/km. Для шестифазной линии (две соединенные трехфазные схемы) эта настройка представляет индуктивность положительной последовательности и нулевой последовательности схемы 1, взаимную индуктивность нулевой последовательности между схемой 1 и схемой 2 и индуктивность положительной последовательности и нулевой последовательности схемы 2.
`C10`	Для трехфазной линии эта настройка представляет емкости положительной последовательности и нулевой последовательности в Farads/km. Для шестифазной линии (две соединенные трехфазные схемы) эта настройка представляет емкости положительной последовательности и нулевой последовательности схемы 1, взаимную емкость нулевой последовательности между схемой 1 и схемой 2 и емкости положительной последовательности и нулевой последовательности схемы 2.

LDATA = power_lineparam('MYLINEDATA') вычисляет параметры линии RLC для параметров геометрической линии в указанном файле. 'MYLINEDATA' - имя MAT-файла. MAT-файл должен содержать структурную переменную того же формата, что и LDATA переменная.

power_lineparam(LDATA,'BLK'), и power_lineparam('MYLINEDATA','BLK') загрузить параметры линии RLC в указанный блок PI Section Line, PI Section Cable, Distributed Parameters Line или Three-Phase PI Section Line. 'BLK' - путь к блоку, имени.

The power_lineparam функция вычисляет матрицы сопротивления, индуктивности и емкости произвольного расположения проводников воздушной линии электропередачи. Для трехфазной линии также вычисляются значения RLC симметричного компонента.

Следующий рисунок показывает типичное расположение проводников для трехфазной двухконтурной линии. Это строение линии иллюстрирует различные параметры линии, которые вы задаете в LDATA структура.

Строение трехфазной двухконтурной линии

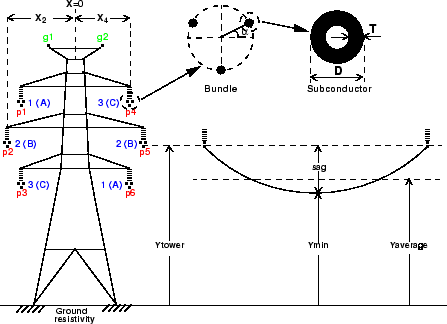
Для набора N проводников, power_lineparam вычисляет три N -by - N матрицы: последовательное сопротивление и индуктивность матриц [R] и [L] и шунтирующую емкостную матрицу [C]. Эти матрицы требуются блоком Distributed Parameters Line для моделирования N -фазных асимметричных линий и однофазным блоком PI Section Line. power_lineparam также вычисляет параметры RLC симметричного компонента, требуемые блоком Three-Phase PI Section Line. Для двух связанных проводников i и k, собственные и взаимные условия матриц R, L и C вычисляются с помощью концепции проводников изображений [1].

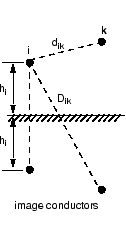
Условия собственного и взаимного сопротивления:

$\begin{matrix} R_{i i} = R_{int} + Δ R_{i i} & Ω / км \end{matrix}$

$\begin{matrix} R_{i k} = Δ R_{i k} & Ω / км \end{matrix}$

Условия собственной и взаимной индуктивности:

$\begin{matrix} L_{i i} = L_{int} + \frac{μ_{0}}{2 π} \cdot \log \frac{2 h_{i}}{r_{i}} + Δ L_{i i} & H / км \end{matrix}$

$\begin{matrix} L_{i k} = \frac{μ_{0}}{2 π} \cdot \log \frac{D_{i k}}{d_{i k}} + Δ L_{i k} & H / км \end{matrix}$

Условия собственных и взаимных потенциальных коэффициентов:

$\begin{matrix} P_{i i} = \frac{1}{2 π ε_{0}} \cdot \log \frac{2 h_{i}}{r_{i}} & км / F \end{matrix}$

$\begin{matrix} P_{i k} = \frac{1}{2 π ε_{0}} \cdot \log \frac{D_{i k}}{d_{i k}} & км / F \end{matrix}$

$\begin{matrix} [C] = {[P]}^{- 1} & F / км \end{matrix}$

где:

_мк0 - проницаемость свободного пространства = 4⁻⁴ Н/км
_ɛ0 - диэлектрическая проницаемость свободного пространства = 8,8542,10⁻⁹ F/км
_ri - радиус проводника i в метрах
_dik - расстояние между проводниками i и k, в метрах
_Дик - это расстояние между проводником i и изображением k, в метрах
_hi - средняя высота проводника i над землей, в метрах
Ринт, Линт являются внутренним сопротивлением и индуктивностью проводника
_{Α Rii}, _{и, как правило, это} условия коррекции Карсона R из-за удельного сопротивления грунта
_{Α Lii}, и, как правило, в коррекцию Карсона L из-за удельного сопротивления земли

Самоиндуктивность проводника вычисляется из магнитного потока, циркулирующего внутри и снаружи проводника, и генерируется током, протекающим в самом проводнике. Часть потока, циркулирующая внутри проводящего материала, способствует внутренней индуктивности Линта, которая зависит от геометрии проводника. Принимая полый или сплошной проводник, внутренняя индуктивность вычисляется из отношения T/D, где D является диаметром проводника, а T является толщиной проводящего материала. См. рисунок Строение трехфазной двухконтурной линии. Самоиндуктивность проводника вычисляется с помощью модифицированных функций Бесселя из диаметра проводника, отношения T/D, сопротивления и относительной проницаемости проводящего материала и заданной частоты [1].

Самоиндуктивность проводника также может быть вычислена из параметров, которые обычно встречаются в таблицах, предоставленных производителями проводников: Geometric Mean Radius (GMR) или «Reactance at one-foot spacing».

GMR является радиусом эквивалентного полого проводника с нулевой толщиной, не производя внутреннего потока, что дает ту же самокорректированность. Самоиндуктивность проводника затем получают из GMR с помощью следующего уравнения:

$\begin{matrix} L_{i i} = \frac{μ_{0}}{2 π} \cdot \log \frac{2 h_{i}}{G M R} + Δ L_{i i} & H / км \end{matrix}$

Для твердого проводника (T/D = 0,5), GMR является

$G M R = r \cdot e^{- μ_{r} / 4}$

r = радиус проводника

_μr = относительная проницаемость проводящего материала

GMR, полученный из этого уравнения, принимает равномерную плотность тока в проводнике. Это предположение строго справедливо в DC. В AC GMR немного выше. Для примера, для твердого алюминиевого проводника диаметром 3 см (Rdc = 0,040 Ом/км), GMR увеличений от 1,1682 см в DC до 1,1784 см при 60 Гц. Производители обычно дают GMR в системе номинальную частоту (50 Гц или 60 Гц).

Реактивное сопротивление _Xa на 1-футовом интервале (или 1-метрового интервала, если используются метрические модули) является реактивным сопротивлением положительной последовательности трехфазной линии, имеющей интервал между тремя фазами и бесконечными высотами проводников на один фут (или один метр). Реактивное сопротивление на 1-футовом интервале (или 1-метрового интервала) на частоте f связано с GMR следующим уравнением:

$\begin{matrix} X_{a} = ω \cdot \frac{μ_{0}}{2 π} \cdot \log \frac{1}{G M R} & Ω / км \end{matrix}$

GMR = Средний геометрический радиус в футах или метрах

.r= 2, f в рад/с

f = частота в герц

Матрица сопротивления проводника на определенной частоте зависит от сопротивления постоянного тока проводника, скорректированного с учетом эффекта кожи и сопротивления земли. И матрица сопротивления, и индуктивная матрица зависят от сопротивления земли и частоты. Условия коррекции для терминов R и L, разработанные Дж. Р. Карсоном в 1926 году [2], реализованы в power_lineparam.

Примеры

В первом примере используется простая линия, состоящая из двух проводников, разнесенных на 1 метр на средней высоте 8 метров над идеальным грунтом (удельное сопротивление земного штока _{β g}= 0). Два проводника являются сплошными алюминиевыми проводниками (удельное сопротивление _{и с}= 28,3 10⁻⁹ А: М на 20^º C), которые имеют диаметр 15 мм.

Сопротивление постоянного тока на км каждого проводника:

$\begin{matrix} r = \frac{ρ_{c} \cdot l}{A} = \frac{28.3 \times 10^{- 9} \times 1000}{π \cdot {(\frac{15 \times 10^{- 3}}{2})}^{2}} = 0.1601 & Ω / км \end{matrix}$

Поскольку заземление должно быть совершенным, диагональные условия матрицы R равны нулю, а диагональные условия представляют сопротивления проводника:

$R = [\begin{matrix} 0.1601 & 0 \\ 0 & 0.1601 \end{matrix}] Ω / км$

Для твердых проводников GMR является:

$\begin{matrix} G M R = r \cdot e^{- μ_{r} / 4} = \frac{1.5}{2} e^{- 1 / 4} = 0.5841 & cm \end{matrix}$

Само- и взаимные индуктивности вычисляются следующим образом. Условия коррекции ÜL игнорируются, потому что сопротивление земли равняется нулю.

$\begin{matrix} L_{11} = L_{22} = \frac{μ_{0}}{2 π} \cdot \log \frac{2 h_{i}}{G M R} = 2 \times 10^{- 4} \log \frac{2 \times 8}{0.5841 \times 10^{- 2}} = 1.583 \times 10^{- 3} H / км \\ L_{12} = L_{21} = \frac{μ_{0}}{2 π} \cdot \log \frac{D_{12}}{d_{12}} = 2 \times 10^{- 4} \log \frac{\sqrt{16^{2} + 1}}{1} = 0.5549 \times 10^{- 3} H / км \\ L = [\begin{matrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{matrix}] = [\begin{matrix} 1.583 \times 10^{- 3} & 0.5549 \times 10^{- 3} \\ 0.5549 \times 10^{- 3} & 1.583 \times 10^{- 3} \end{matrix}] H / км \end{matrix}$

Само- и взаимные емкости вычисляются следующим образом:

$\begin{matrix} P_{11} = P_{22} = \frac{1}{2 π ε_{o}} \log \frac{2 h}{r_{i}} = 1.7975 \times 10^{7} \log \frac{2 \times 8}{0.75 \times 10^{- 2}} = 1.3779 \times 10^{8} км/Ф \\ P_{12} = P_{21} = \frac{1}{2 π ε_{o}} \log \frac{D_{12}}{d_{12}} = 1.7975 \times 10^{7} \log \frac{\sqrt{16^{2} + 1}}{1} = 4.9872 \times 10^{7} км/Ф \\ C = {[\begin{matrix} P_{11} & P_{12} \\ P_{21} & P_{22} \end{matrix}]}^{- 1} = [\begin{matrix} 8.352 \times 10^{- 9} & - 3.023 \times 10^{- 9} \\ - 3.023 \times 10^{- 9} & 8.352 \times 10^{- 9} \end{matrix}] F / км \end{matrix}$

Сначала вы создаете шаблон LDATA структура для определения геометрии линий и типа проводников этой линии. В MATLAB^® приглашение, введите:

LDATA = power_lineparam('new');

Затем установите следующие поля с определенными значениями:

 LDATA.frequency = 50;
 LDATA.groundResistivity = 0;
 LDATA.Geometry.NPhaseBundle = 2;
 LDATA.Geometry.NGroundBundle = 0;
 LDATA.Geometry.PhaseNumber = [1,2];
 LDATA.Geometry.X = [0,1];
 LDATA.Geometry.Ytower = [8,8];
 LDATA.Geometry.Ymin = [8,8];
 LDATA.Geometry.ConductorType = [1,1];
 % define conductor Type 1:
 LDATA.Conductors.Diameter = [1.5];
 LDATA.Conductors.ThickRatio = [0.5];
 LDATA.Conductors.GMR = [0.5841];
 LDATA.Conductors.Res = [0.1601];
 LDATA.Conductors.Mur = [1];
 LDATA.Conductors.Nconductors = [1];
 LDATA.Conductors.BundleDiameter =[0];
 LDATA.Conductors.AngleConductor1 = [0];
 LDATA.Conductors.skinEffect = 'no';

Затем вы вычисляете параметры линии RLC с помощью команды:

 LDATA = power_lineparam(LDATA);
 disp(LDATA.R),disp(LDATA.L),disp(LDATA.C)

Модель PI для линии 1 км получена из матриц R, L и C. Значения PI RLC получают из само- и взаимных терминов матриц R, L и C. Нижние индексы s и m обозначают само- и взаимные условия в матрицах R, L и C.

R _p1 = _R p2 = R s = 0,1601

L _p1 = _L p2 = L s = 1,583 мГ/км

C _p1 = _C p2 = C s ₊ C m = 8,352 - 3,023 = 5,329 нФ/км (2,664 нФ на каждом конце секции ПИ)

C _p1p2 = – C m = 3,023 нФ/км (1,511 нФ на каждом конце секции ПИ)

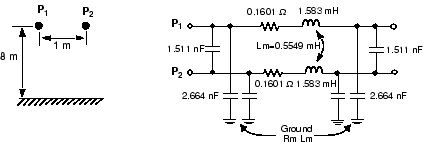
Можно также изменить сопротивление земли и частоту, чтобы наблюдать их влияние на сопротивление и индуктивность проводника и возврата земли.

Следующий код изменяет сопротивление земли от нуля до 10000

Rground = [0,10,100,10000]
for k=1:4
   LDATA.groundResitivity = Rground(k);
   LDATA = power_lineparam(LDATA);
   ConductorRS_RM(k) = LDATA.R(1,1)-LDATA.R(1,2);
   GroundRm(k) = LDATA.R(1,2);
   ConductorLs_Lm(k) = LDATA.L(1,1)-LDATA.L(1,2);
   GroundLm(k) = LDATA.L(1,2);
end

Вы должны получить значения, перечисленные в следующей таблице. Выражения Rs-Rm и Ls-Lm представляют соответственно сопротивление и индуктивность проводника, тогда как Rm и Lm являются сопротивлением и индуктивностью возврата земли.

Влияние сопротивления грунта (частота = 50 Гц; Эффект кожи не включен)

Земля Удельное сопротивление (	Проводник Rs-Rm (А/км)	Земля Комната (А/км)	Проводник Ls-Lm (мГ/км)	Земля Lm (мГ/км)
0	0.1601	0	1.028	0.5549
10	0.1601	0.04666	1.029	1.147
100	0.1601	0.04845	1.029	1.370
10 000	0.1601	0.04925	1.029	1.828

Когда удельное сопротивление грунта изменяется в нормальном диапазоне (между 10 и 10 м для влажного грунта и 10 000 И м для сухого скального грунта), сопротивление грунта остается почти постоянным на уровне 0,05 Ом/км, в то время как его индуктивность увеличивается с 1,15 мГ/км до 1,83 мГ/км.

Используя следующий код, повторите расчет с различными частотами в диапазоне от 0,05 Гц до 50 кГц и эффектом кожи проводника, смоделированным для сопротивления земли 100 Ом-м.

LDATA.groundResitivity = 100;
Frequencies = [0.05,50,500,5000,50000]
for k=1:5
   LDATA.frequency = Frequencies(k);
   LDATA = power_lineparam(LDATA);
   ConductorRS_RM(k) = LDATA.R(1,1)-LDATA.R(1,2);
   GroundRm(k) = LDATA.R(1,2);
   ConductorLs_Lm(k) = LDATA.L(1,1)-LDATA.L(1,2);
   GroundLm(k) = LDATA.L(1,2);
end

Влияние частоты (сопротивление земли = 100 с эффектом кожи проводника)

Частота (Гц)	Проводник Rs-Rm (А/км)	Земля Комната (А/км)	Проводник Ls-Lm (мГ/км)	Земля Lm (мГ/км)
0.05	0.1601	4.93e-5	1.029	2.058
50	0.1606	0.04844	1.029	1.370
500	0.2012	0.4666	1.022	1.147
5000	0.5442	4.198	0.9944	0.9351
50 000	1.641	32.14	0.9836	0.7559

Эта таблица показывает, что частота оказывает очень большое влияние на сопротивление земли, но гораздо меньшее влияние на индуктивность земли. Из-за эффекта кожи в земле, когда частота увеличивается, ток заземления течёт ближе к поверхности, уменьшая эквивалентную секцию заземляющего проводника и тем самым увеличивая его сопротивление. Когда ток земли перемещается на меньшей глубине на высоких частотах, индуктивность цикла проводника плюс возврат земли (или самоиндуктивность, Ls) уменьшается.

Из-за эффекта кожи проводника частота оказывает заметное влияние на сопротивление проводника от нескольких сотен герц, но незначительное влияние на индуктивность проводника. При номинальной частоте системы (50 Гц или 60 Гц) увеличение сопротивления проводника по отношению к сопротивлению постоянному току (0,1601 Ом/км) составляет всего 0,3%.

Второй пример соответствует трехфазной двухконтурной линии на 500 кВ.

Степень передается по шести фазы проводникам, образующим две трехфазные схемы. Линия защищена от молний двумя проводами заземления. Проводники фазы используют пучки из трех субпроводников. Субпроводники расположены на верхней части раверального треугольника 50-см сторон, соответствующего диаметру пучка 57,735 см. Эта конфигурация линии соответствует строению, показанной на рисунке Строении трехфазной двухконтурной линии.

Нумерация фазы была установлена, чтобы получить линейные параметры трехфазной линии, эквивалентной двум схемам, соединенным параллельно. В Compute разделе щелкните RLC Line Parameters, чтобы отобразить матрицы R, L и C и параметры последовательности.

Параметры положительной и нулевой последовательностей транспонированной линии отображаются в разделе Computed Parameters в векторах R10 и L10:

R1 = 0,009009 И/км R0 = 0,2556 И/км

L1 = 0,4408 мГ/км L0 = 2,601 мГ/км

C1 = 25,87 нФ/км C0 = 11,62 нФ/км

Можно также получить параметры двух отдельных схем и получить доступ к шести проводникам фазы. Измените число фаз проводников p4, p5 и p6 (схема 2) на 6, 5 и 4, соответственно. Параметры положительной последовательности, нулевой последовательности и взаимной нулевой последовательности транспонированной линии:

R1 = 0,01840 В/км R0 = 0,2649 В/км R0m = 0,2462 В/км

L1 = 0,9296 мГ/км L0 = 3,202 мГ/км L0m = 2,0 мГ/км

C1 = 12,57 нФ/км C0 = 7,856 нФ/км C0m = − 2.044 нФ/км

Поскольку линия симметрична, параметры положительной и нулевой последовательности для схемы 2 идентичны параметрам схемы 1.

Ссылки

[1] Dommel, H. et al., Electromagnetic Transitions Program Reference Manual (EMTP Theory Book), 1986.

[2] Carson, J. R., «Wave Propagation in Overhead Wires With Ground Return», Bell Systems Technical Journal, Vol. 5, pp 539-554, 1926.

См. также

Distributed Parameters Line | PI Section Line | Power Line Parameters | Powergui | Three-Phase PI Section Line

Документация