Синхронный двигатель с постоянными магнитами, заданный в терминах магнитного потокосцепления
Simscape/Электрический/Электромеханический/Постоянный магнит
Блок FEM-Parameterized PMSM реализует модель синхронного двигателя с постоянными магнитами (PMSM), заданную в терминах магнитного потокосцепления. Вы параметризоваете блок, предоставляя табличные данные магнитного потока двигателя как функции тока и угла ротора. Это способ, которым сторонние пакеты магнитного метода с конечными элементами (FEM) обычно экспортируют информацию о потоке. Из-за сведенной в табличной формы поток может изменяться нелинейным образом как на угол ротора, так и на ток. Поэтому можно использовать этот блок для моделирования PMSM с трапециевидным профилем коэффициента противо-ЭДС, иногда называемым бесщеточным двигателем постоянного тока, а также обычным PMSM.
Рисунок показывает эквивалентную схему для PMSM с соединением wye. Угол ротора равен нулю, когда поток постоянных магнитов выравнивается с магнитной осью А-фазы.
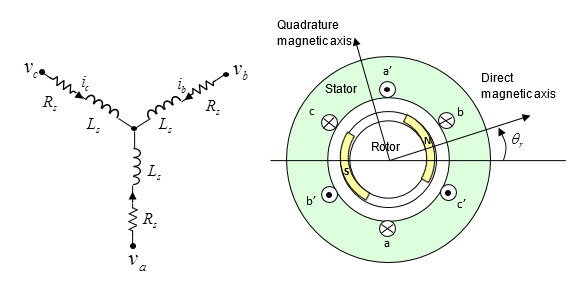
На практике потокосцепление каждой из трех обмоток зависит от всех трех токов и угла ротора. Табуляция потока как функции четырех независимых переменных может привести к неэффективности симуляции и значительным требованиям к памяти для управления данными. Поэтому блок позволяет вам выбрать между следующими методами параметризации для потока и крутящего момента:
2-D partial derivative data - 2-D поиск таблицы, с опциями, которые можно свести в таблицу с точки зрения тока и угла ротора, или с точки зрения d-ось и q-токи по оси. Первая опция принимает постоянную взаимную индуктивность и поддерживает несинусоидальные профили заднего ЭДС. Вторая опция принимает синусоидальный обратный ЭДС и захватывает эффекты насыщения для внутренних PMSM (IPMSM).
3-D partial derivative data - 3-D поиск таблицы, основанный на постоянном токе, квадратурном токе и угле ротора. Вы предоставляете данные поиска потока для фазы a. Блок использует преобразование Park, чтобы сопоставить три тока обмотки статора с прямыми и квадратурными токами. Этот метод уменьшает сложность данных по сравнению с поиском в 4-D таблице и, следовательно, приводит к улучшению эффективности симуляции.
4-D partial derivative data - 4-D просмотр таблицы, основанный на трех токах обмотки статора и угле ротора. Вы предоставляете данные поиска потока для фазы a. Эта модель имеет лучшую точность из трех, но также является наиболее затратной с точки зрения эффективности симуляции и требований к памяти.
3-D flux linkage data - 3-D поиск таблицы, основанный на данных о редактировании потока. Вы можете предоставить данные редактирования потока в различных форматах. Блок использует преобразование Park, чтобы сопоставить три тока обмотки статора с прямыми и квадратурными токами. Этот метод уменьшает сложность данных по сравнению с поиском в 4-D таблице и, следовательно, приводит к улучшению эффективности симуляции.
По умолчанию все варианты блока осуществляют строение раны Уая для обмоток статора. Однако возможно переключение на дельта-обмотку строения, выбираемую с помощью параметра Winding type. Когда в строении дельта-обмотки фаза a соединяется между портами a и b, фаза b между портами b и c и фаза c между портами c и a.
Чтобы получить доступ к этим методам параметризации, щелкните правой кнопкой мыши блок в модели, выберите Simscape > Block choices, а затем выберите требуемый вариант блока с тепловыми портами или без них. По умолчанию тепловые порты не являются пустыми. Для получения дополнительной информации см. Раздел «Тепловые порты»
В этой модели данных о 2-D потоке поток, связывающий каждую обмотку, принимается нелинейно зависящим только от тока в этой же обмотке, плюс угол ротора. На практике это разумное предположение для многих синхронных двигателей с постоянными магнитами; однако он менее точен для переключаемых реактивных двигателей. Учитывая это предположение, потоки в трех обмотках:
где - редактирование потока для обмотки A-фазы как функции от угла ротора и тока A-фазы. Θ r = 0 соответствует ротору d-ось, выравнивающаяся по положительному направлению магнитного потока A-фазы. M s является взаимной индуктивностью статор-статор.
Для улучшения численной эффективности, уравнения, реализованные в блоке, фактически работают с частными производными редактированиями потока относительно тока, , и угол ротора, , а не поток непосредственно. Если ваш пакет КЭМ не экспортирует эти частные производные, можно определить их с помощью MATLAB® скрипт. Смотрите Solenoid Parameterized с примером модели FEM Data и его поддерживающим скриптом MATLAB для примера того, как это сделать.
Электрические уравнения для блока, заданные в терминах частных производных потока, являются:
где
v a, v b, v c являются напряжениями, приложенными к обмоткам статора A, B и C.
i a, i b, i c являются токами статора в каждой из трех обмоток.
R s - сопротивление каждой из обмоток статора.
M s является взаимной индуктивностью статор-статор.
являются частными производными редактированиями потока относительно тока статора в каждой из трех обмоток.
- частное производное редактирование потока относительно угла ротора.
Блок может автоматически вычислить матрицу крутящего момента из информации о потоке, которую вы предоставляете. Кроме того, можно задать параметр Calculate torque matrix? равным No и непосредственно задайте крутящий момент как функцию тока и угла ротора. Для получения дополнительной информации см. FEM-Parameterized Rotary Actuator страницы с описанием блоков.
В этой модели данных о 2-D потоке поток, связывающий каждую обмотку, принимается нелинейно зависящим от всех токов обмотки статора, плюс принято, что редактирование потока постоянных магнитов синусоидально. PMSM внутренних магнитов (или IPMSM) обычно хорошо соответствуют этому предположению. Уравнения:
где
i d и i q являются d-ось и q-токи осей, соответственно.
ϕ d и ϕ q являются d-ось и q-осевые потоковые редактирования, соответственно.
ϕ m - потокосцепление с постоянными магнитами.
L d и L q являются d-ось и q- составляющие индукции, соответственно. Они приняты в зависимости от d-ось и q-токи по оси.
N - количество пар полюсов.
T - электрический крутящий момент.
Работа с четырехмерными данными имеет как стоимость эффективности симуляции, так и стоимость памяти. Чтобы уменьшить размерность таблицы до трехмерной, модель 3-D данных использует преобразование Park, чтобы сопоставить три тока с прямыми и квадратурными токами:
В общем случае Park преобразует карты в прямые, квадратурные и токи с нулевой последовательностью. Однако ток нулевой последовательности обычно является маленьким при нормальных рабочих условиях. Поэтому модель пренебрегает зависимостью терминов редактирования потока от тока с нулевой последовательностью и определяет редактирование потока с точки зрения просто прямых и квадратурных токов плюс угол ротора. Уравнение потока для модели 3-D данных:
Электрические уравнения для блока также заданы в терминах частных производных потока, аналогичных модели 4-D данных. Можно вычислить данные 3-D потоке редактирования частной производной от данных о 4-D потоке редактирования используя ee_calculateFluxPartialDerivatives.
Потокосцепление каждой из обмоток является функцией тока в этой обмотке, токов в двух других обмотках и угла ротора. Для полной точности модель данных о 4-D потоке принимает, что редактирование потока является функцией трех токов и угла ротора, поэтому выполняет четырехмерные интерполяции таблицы. Уравнение потока:
где
ϕ a, ϕ b, ϕ c являются потоковыми редактированиями для обмоток статора A, B и C.
i a, i b, i c являются токами статора в каждой из трех обмоток.
Θ r - угол ротора. Θ r = 0 соответствует случаю, когда поток постоянных магнитов выровнен с потоком обмотки статора А-фазы.
N - количество пар полюсов.
Данные потокосцепления приняты циклическими с Θ r. Если, например, двигатель имеет шесть пар полюсов, то область значений для данных составляет 0 ≤ Θ r ≤ 60 °. Вы должны предоставить данные как в 0, так и в 60 степенях, и, поскольку данные являются циклическими, частные производные редактирования должны быть одинаковыми в этих двух конечных точках.
Уравнение крутящего момента:
Модель 4-D данных не имеет опции для блока, чтобы определить крутящий момент от редактирования. Из-за увеличения численных накладных расходов в 4-D случае лучше предварительно вычислить крутящий момент всего один раз, чем вычислять его каждый раз, когда вы запускаете симуляцию.
Для улучшения численной эффективности, уравнения, реализованные в блоке, фактически работают с частными производными редактированиями потока относительно трех токов и угла ротора, а не непосредственно потока. Если ваш пакет КЭМ не экспортирует эти частные производные, можно определить их с помощью ee_calculateFluxPartialDerivatives.
Электрические уравнения для блока, заданные в терминах частных производных потока, являются:
где
v a, v b, v c являются напряжениями, приложенными к обмоткам статора A, B и C.
i a, i b, i c являются токами статора в каждой из трех обмоток.
R s - сопротивление каждой из обмоток статора.
Опции 3-D данных о редактировании потока позволяют вам работать с необработанными данными о редактировании потока, экспортированными из Design Tool двигателя с конечными элементами (FE). Это в отличие от 3-D опций данных частной производной, для которых вам нужно определить частные производные. Вы можете предоставить данные редактирования потока в различных форматах, для поддержки различных соглашений об инструментах FE:
Табуляция данных о редактировании потока осей DQ или данных о редактировании потока фазы A - Некоторые инструменты поддержки работу с редактированиями потока, разрешенными в прямые (D) и квадратурные (Q) оси. Преимущество этого подхода заключается в том, что необходимы данные для углов ротора в область значений 0 к 360/ N/3 степеней (где N - количество пар полюсов). Другие инструменты работают непосредственно со потоками A-, B- и C-фазы, и для этого можно импортировать только потокосцепление A-фазы, для которого диапазон углов ротора должен быть в диапазоне от 0 до 360/ N градусов. Неявное предположение импорта только данных A-фазы состоит в том, что данные B и C фазы одинаковы, кроме сдвинутых по фазе.
Табуляция с использованием декартовых или полярных координат тока - Декартова табуляция подразумевает, редактирование поток сведен в таблицы с точки зрения тока оси D и тока оси Q (плюс угол ротора). В качестве альтернативы, полярная табуляция включает в себя табличные редактирования потока с точки зрения величины тока, угла усовершенствования тока относительно оси Q и угла ротора. Преимущество полярных координат в том, что он более естественно отражает разрешенные рабочие токи, таким образом избегая неиспользованных точек данных таблицы.
Эти соглашения приводят к четырем Flux linkage data format опциям параметризации:
D and Q axes flux linkages as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta)
D and Q axes flux linkages as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta)
A-phase flux linkage as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta)
A-phase flux linkage as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta)
Помимо выбора формата данных редактирований потоком, используемого вашим инструментом FE, необходимо выбрать версию преобразования Park, используемую инструментом. Четыре соглашения описаны ниже и соответствуют четырем опциям для раскрывающегося меню Park’s convention for tabulated data.
Примечание
При рассмотрении записанных значений для токов D- и Q-осей имейте в виду, что для каждой из этих опций формат преобразуется по мере необходимости, так что внутренне блок FEM-Parameterized PMSM последовательно использует Вариант 1.
Это конвенция Парка, используемая внутренне при Simscape™ Electrical™ моторных и машинных блоков. Все остальные опции преобразуются в этот формат.
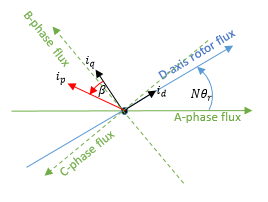
N: количество пар полюсов
θ r: угол ротора
i d, i q: токи осей D и Q
i p: Текущая величина =
β: Угол усовершенствования тока =
Соответствующее преобразование Парка является
где i a, i b и i c являются токами A-фазы, B-фазы и C-фазы, соответственно.
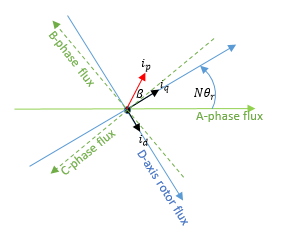
N: количество пар полюсов
θ r: угол ротора
i d, i q: токи осей D и Q
i p: Текущая величина =
β: Угол усовершенствования тока =
Соответствующее преобразование Парка является
где i a, i b и i c являются токами A-фазы, B-фазы и C-фазы, соответственно.
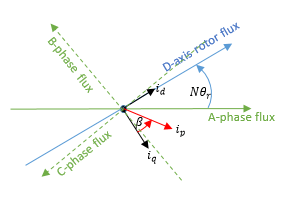
N: количество пар полюсов
θ r: угол ротора
i d, i q: токи осей D и Q
i p: Текущая величина =
β: Угол усовершенствования тока =
Соответствующее преобразование Парка является
где i a, i b и i c являются токами A-фазы, B-фазы и C-фазы, соответственно.
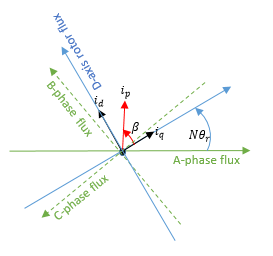
N: количество пар полюсов
θ r: угол ротора
i d, i q: токи осей D и Q
i p: Текущая величина =
β: Угол усовершенствования тока =
Соответствующее преобразование Парка является
где i a, i b и i c являются токами A-фазы, B-фазы и C-фазы, соответственно.
Блок FEM-Parameterized PMSM моделирует потери в железе согласно методам параметризации, которые вы выбираете для потока и крутящего момента.
Для 2-D partial derivative data, 3-D partial derivative data и 4-D partial derivative data опций с тепловыми портами или без них потерей в железе модель основана на работе Меллора [1]. Потери в железе разделены на два члена, один из которых представляет основную траекторию намагничивания, а другой представляет траекторию поперечного совета зуба, которая становится активной во время ослабленных операций поля.
Термин, представляющий основной путь намагниченности, зависит от индуцированного напряжения статора RMS, :
Это доминирующий термин во время работы без нагрузки. k является коэффициентом противо-ЭДС, постоянная, относящимся к RMS В на Гц. Он определяется как , где f является электрической частотой. Первый член на правой стороне является потерей магнитного гистерезиса, второй - потеря токов Фуко, третий - избыточные потери. Три коэффициента, появляющиеся на числителях, получают из значений, которые вы обеспечиваете для гистерезиса без обратной связи, вихря и избыточных потерь.
Термин, представляющий путь совета поперек зуба, становится важным, когда устанавливается поле размагничивания, и может быть определен из анализа короткой схемы тестирования конечного элемента. Это зависит от RMS ЭДС, связанной с потоком поперечных советов, :
Три члена числителя получают из значений, которые вы обеспечиваете для гистерезиса короткой схемы, вихря и избыточных потерь.
Для 3-D flux linkage data с тепловыми портами или без них можно также смоделировать потери в железе на основе уравнения Штейнметца. Метод Штейнметца масштабируется для различных скоростей двигателя или электрических частот, так что данные потерь в железе требуются только как функция токов двигателя. Если вы устанавливаете параметр Iron losses modeling равным Specify open and short circuit loss data (permanent magnet motors only)блок использует метод Штейнметца, но принимает постоянные коэффициенты и отсутствие зависимости от пиковых фаз тока и усовершенствования тока. И наоборот, если вы задаете значение параметра Flux linkage data format D and Q axes flux linkages as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta) или A-phase flux linkage as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta) , затем блок свел коэффициенты с параметрами Peak current magnitude vector, I и Current advance angle vector, B, так что потери в железе заданы:
где:
f - электрическая частота, в Hz.
khr(Ip,β) является Rotor hysteresis loss coefficient, k_hr(I,B).
kJr(Ip,β) является Rotor eddy current loss coefficient, k_Jr(I,B).
ker(Ip,β) является Rotor excess current loss coefficient, k_er(I,B).
khs(Ip,β) является Stator hysteresis loss coefficient, k_hs(I,B).
kJs(Ip,β) является Stator eddy current loss coefficient, k_Js(I,B).
kes(Ip,β) является Stator excess current loss coefficient, k_es(I,B).
Точно так же, если вы задаете значение параметра Flux linkage data format D and Q axes flux linkages as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta) или A-phase flux linkage as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta), затем потери в железе даются:
где:
khr(iD,iQ) является Rotor hysteresis loss coefficient, k_hr(iD,iQ).
kJr(iD,iQ) является Rotor eddy current loss coefficient, k_Jr(iD,iQ).
ker(iD,iQ) является Rotor excess current loss coefficient, k_er(iD,iQ).
khs(iD,iQ) является Stator hysteresis loss coefficient, k_hs(iD,iQ).
kJs(iD,iQ) является Stator eddy current loss coefficient, k_Js(iD,iQ).
kes(iD,iQ) является Stator excess current loss coefficient, k_es(iD,iQ).
Блок имеет четыре дополнительных тепловых порта, по одному для каждой из трех обмоток и по одному для ротора. Эти порты по умолчанию скрыты. Чтобы выставить тепловые порты, щелкните правой кнопкой мыши по блоку в своей модели, выберите Simscape> Block choices и затем выберите желаемый вариант блока с тепловыми портами: 2-D partial derivative data | Show thermal port, 3-D partial derivative data | Show thermal port, 4-D partial derivative data | Show thermal port, или 3-D flux linkage data | Show thermal port. Это действие отображает тепловые порты на значке блока и отображает параметры Temperature Dependence и Thermal Port. Эти параметры описаны далее на этой странице с описанием.
Используйте тепловые порты, чтобы симулировать эффекты сопротивления меди и потерь в железе, которые преобразуют электрические степени в тепло. Для получения дополнительной информации об использовании тепловых портов в блоках привода, смотрите Симуляция термальных эффектов во Вращательном и Поступательном приводах.
Этот блок имеет следующие ограничения:
Для модели 2D данных взаимная индуктивность статор-статор, заданная Stator mutual inductance, Ms значением параметров, является постоянной во время симуляции и не изменяется с углом ротора. Это означает, что блок подходит для моделирования большинства PMSM и бесщеточных двигателей постоянного тока, но не коммутируемых реактивных двигателей.
Модели 3-D и 4-D данных предполагают симметрию, так что зависимость редактирования потока от токов и угла ротора для обмоток B и C может быть определена из зависимости для обмотки A.
Для модели 4-D данных учитывайте требования памяти при фиксации независимых значений параметров (три тока и углы ротора). Опция линейной интерполяции использует меньше памяти, но опция сплайна-интерполяции более точна для заданного независимого интервала параметров.
Модель потерь в железе принимает синусоидальные токи.
[1] Меллор, П.Х., Р. Вробель и Д. Холлидей. «Вычислительно эффективная модель потери в железе для бесщеточных машин переменного тока, которая удовлетворяет номинальным потокам и полевым ослабленным операциям». Конференция по электрическим машинам и приводам IEEE. Май 2009.
ee_calculateFluxPartialDerivatives | FEM-Parameterized Linear Actuator | FEM-Parameterized Rotary Actuator