Luenberger Observer

Наблюдатель Luenberger в дискретном времени

Библиотека:
Simscape / Электрический / Контроль / Наблюдатели

Описание

Блок Luenberger Observer реализует наблюдателя Luenberger в дискретном времени. Используйте этот блок для оценки состояний наблюдаемой системы с помощью:

Дискретные входы и выходы системы.
Дискретное представление системы в пространстве состояний.

Luenberger Observer также иногда упоминается как государственный наблюдатель или просто как наблюдатель.

Можно управлять мультивходами, несколькими выходами путем передачи вектора выходного состояния этого блока в блок State Feedback Controller.

Определение уравнений

Блок реализует дискретное время Luenberger Observer с использованием обратного метода Эйлера из-за его простоты и устойчивости.

Оценка задается этим разностным уравнением:

$\hat{x} (k + 1) = A_{d} \hat{x} (k) + B_{d} u (k) + L_{d} (y (k) - \hat{y} (k)),$

где:

$\hat{x} (k)$ является k^th вычисленный вектор состояния.
$\hat{y} (k)$ является k^th вычисленный выходной вектор.
u(k) является k^th входной вектор.
y(k) является k^th измеренный выходной вектор.
_Ad - дискретизированная матрица состояний.
_Bd - дискретизированная входная матрица.
_Ld - дискретизированная матрица усиления наблюдателя.

Динамика ошибки расчета описывается:

$e (k + 1) = (A_{d} - L_{d} C_{d}) e (k),$

где:

e(k) является k^th вектор ошибок.
_Cd - выходная матрица.

Ошибка расчета сходится к нулю, когда _Ad-LdCd имеет свои собственные значения внутри модуля круга. Поэтому значение _Ld должна быть такой, чтобы эта цель была достигнута. Блок вычисляет коэффициент усиления наблюдателя путем решения

$L_{d}^{T} = G X^{- 1},$

где G является произвольной матрицей, и X получается путем решения уравнения Сильвестра:

$A_{d}^{T} X - X Λ = C_{d}^{T} G .$

Здесь Λ матрица с желаемыми собственными значениями, которые не совпадают с собственными значениями _Ad. Эта схема показывает базовую структуру дискретного времени Luenberger Observer.

Предположения

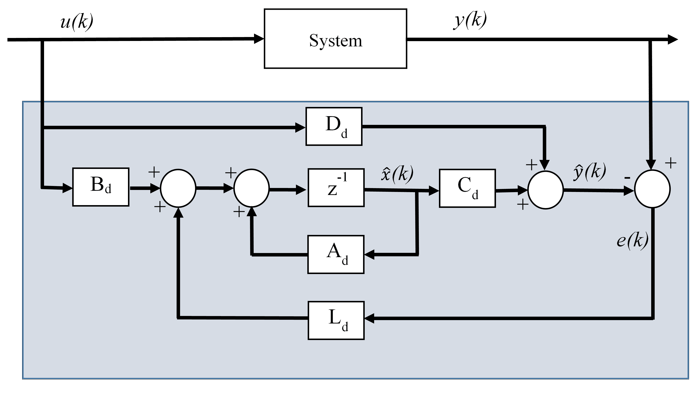
Система наблюдаема, что верно, если состояние системы может быть определено из входа и выхода за конечное время. Математически это означает, что матрица наблюдаемости системы имеет полный ранг.

Ограничения

Желаемые собственные значения не совпадают с собственными значениями модели без разомкнутого контура.

Порты

Вход

расширить все

`u` - Управляющий вход
вектор

Входной сигнал в систему, состояние которой мы хотим оценить, заданный как вектор.

Типы данных: single | double

`y` - Выходные данные системы
вектор

Измеренный выход системы, состояние которой мы хотим оценить, задается как вектор.

Типы данных: single | double

Выход

расширить все

`xhat` - Оценка состояния
вектор

Оценка состояния системы, заданная как вектор.

Типы данных: single | double

Параметры

расширить все

`State-space parameterization` - Параметризация пространства состояний
`Discrete-time` (по умолчанию) | `Continuous-time`

Выберите стратегию для параметризации матриц пространства состояний и желаемых полюсов для наблюдателя. Реализация блока дискретна независимо от этой параметризации.

`Discrete A matrix` - Матрица за дискретное время
1 (по умолчанию) | действительный скаляр или матрица

Матрица состояний модели пространства состояний в дискретном времени. Матрица A должна быть квадратной, с количеством строк и столбцов, равным порядку системы.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization равным Discrete-time.

`Discrete B matrix` - матрица B за дискретное время
1 (по умолчанию) | действительный скаляр или матрица

Входная матрица модели пространства состояний в дискретном времени. Матрица B должна иметь количество строк, равное порядку системы, и количество столбцов, равное количеству системных входов.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization равным Discrete-time.

`Discrete C matrix` - матрица C за дискретное время
1 (по умолчанию) | действительный скаляр или матрица

Выходная матрица модели пространства состояний в дискретном времени. Матрица C должна иметь количество строк, равное количеству выходов системы, и количество столбцов, равное порядку системы.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization равным Discrete-time.

`Discrete D matrix` - D-матрица за дискретное время
1 (по умолчанию) | действительный скаляр или матрица

Исходная матрица модели пространства состояний в дискретном времени. D- матрицы должно иметь количество строк, равное количеству системных выходов, и количество столбцов, равное количеству системных входов.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization равным Discrete-time.

`Continuous A matrix` - Матрица за непрерывное время
1 (по умолчанию) | действительный скаляр или матрица

Матрица состояний модели пространства состояний в непрерывном времени. Матрица A должна быть квадратной, с количеством строк и столбцов, равным порядку системы.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization равным Continuous-time.

`Continuous B matrix` - B матрица за непрерывное время
1 (по умолчанию) | действительный скаляр или матрица

Входная матрица модели пространства состояний в непрерывном времени. Матрица B должна иметь количество строк, равное порядку системы, и количество столбцов, равное количеству системных входов.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization равным Continuous-time.

`Continuous C matrix` - матрица C за непрерывное время
1 (по умолчанию) | действительный скаляр или матрица

Выходная матрица модели пространства состояний в непрерывном времени. Матрица C должна иметь количество строк, равное количеству выходов системы, и количество столбцов, равное порядку системы.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization равным Continuous-time.

`Continuous D matrix` - D-матрица за непрерывное время
1 (по умолчанию) | действительный скаляр или матрица

Исходная матрица модели пространства состояний в непрерывном времени. D- матрицы должно иметь количество строк, равное количеству системных выходов, и количество столбцов, равное количеству системных входов.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization равным Continuous-time.

`Observer design` - Параметризация пространства состояний
`Desired eigenvalues` (по умолчанию) | `Observer gain`

Выберите стратегию для параметризации усиления наблюдателя.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization равным Discrete-time.

`Observer gain` - Коэффициент усиления наблюдателя
1 (по умолчанию) | действительный скаляр или матрица

Задайте коэффициент усиления наблюдателя, который помещает все собственные значения матрицы _Ad-LdCd внутрь модуля круга. Матрица усиления должна иметь количество строк, равное количеству системных входов, и количество столбцов, равное порядку системы.

Зависимости

Чтобы включить этот параметр, установите:

State-space parameterization с Discrete-time.
Observer design с Observer gain.

`Desired eigenvalues` - Собственные значения наблюдателя
0 (по умолчанию) | вектор действительных чисел

Укажите местоположение собственных значений:

Иметь отрицательную вещественную часть, если State-space parameterization установлено в Continuous-time. В этом случае собственные значения системы непрерывного времени аппроксимируются к дискретным таковым на основе Discretization sample time.
Чтобы лежать внутри единичного круга, если State-space parameterization установлено в Discrete-time.

Коэффициент усиления Observer затем вычисляется на основе этих собственных значений. Размер вектора должен быть таким же, как и системный порядок.

`Initial conditions` - Начальные условия
0 (по умолчанию) | вектор действительных чисел с длиной, равной системному порядку

Выберите начальное условие каждого состояния.

`Discretization sample time` - Дискретизация шага расчета
0,1 (по умолчанию) | положительное вещественное число

Значение, используемое для дискретизации матриц пространства состояний, а также аппроксимации собственных значений в дискретном времени.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization равным Continuous-time.

`Sample time` - Шаг расчета
0,1 (по умолчанию) | -1 или положительное вещественное число

Значение, используемое для симуляции динамики модели. Выберите то же значение, что и Discretization sample time, если блок не помещен в триггируемую подсистему, в этом случае необходимо установить его на -1.

Примеры моделей

DC Motor Control (State-Feedback and Observer)

Управление двигателем постоянного тока (обратная связь и наблюдатель)

Структура управления скоростью с обратной связью для двигателя постоянного тока. Для питания двигателя постоянного тока используется управляемый ШИМ четырехквадрантный Chopper. Подсистема управления включает цикл управления с обратной связью состояний и генерацию ШИМ. Вектор состояния включает скорость ротора, которая измеряется, и ток двигателя постоянного тока, который оценивается с помощью наблюдателя. И наблюдатель, и контроллер обратной связи состояния синтезируются путем размещения полюса с помощью модели пространства состояний системы. Общее время симуляции (t) составляет 4 секунды. На t = 1,5 секунде крутящий момент нагрузки увеличивается. При t = 2,5 секунд задающей скорости изменяется с 1000 об/мин до 2000 об/мин.

Управление положением PMSM

Управление положением ротора в электроприводе на основе PMSM. Идеальный источник крутящего момента обеспечивает нагрузку. Подсистема управления использует структуру каскадного регулирования с двумя циклами управления, внешний контур для управления положением и скоростью и внутренний цикл для управления током. Оптимальный линейный квадратичный регулятор с обратной связью состояний управляет положением и скоростью. Наблюдатель Luenberger оценивает нагрузку. Внутренний контур управления током реализован с помощью ПИ-контроллеров. PMSM питается управляемым трехфазным инвертором. В симуляции используются ссылки на шаги. Подсистема Возможностей содержит возможности, которые позволяют вам видеть результаты симуляции.

Управление состоянием синхронной машины - Пространство

Управляйте токами в тяговом приводе на основе синхронной машины (SM), используя управление пространством состояний. Высоковольтная батарея подает SM через управляемый трехфазный преобразователь для обмоток статора и через управляемый двухквадрантный измельчитель для обмотки ротора. Идеальный источник скорости вращения обеспечивает нагрузку. SM работает ниже номинальной скорости. В каждый момент выборки запрос крутящего момента преобразуется в соответствующие ссылки тока с помощью подхода управления осью нуля d-составляющей. Контроллер обратной связи состояния управляет токами в исходной системе координат ротора. Наблюдатель Luenberger получает зависящие от скорости условия предварительного контроля с feedforward. В симуляции используется несколько шагов крутящего момента как в режиме двигателя, так и в режиме генератора. Планирование задач реализовано как конечный автомат Stateflow ®. Подсистема Возможностей содержит возможности, которые позволяют вам видеть результаты симуляции.

Ссылки

[1] Luenberger, D. G. «An Introduction to Observers». Транзакции IEEE по автоматическому управлению. Том 16, № 6, 1971, стр. 596-602.

[2] Алессандри, А. и П. Колетта. «Проект наблюдателей Luenberger для класса гибридных линейных систем». Международный практикум по гибридным системам: Расчеты и управление, Берлин, март 2001 года.

[3] Варга, А. «Назначение робастного шеста через параметризацию обратной связи на основе уравнения Сильвестра». В Computer-Aided Control System Design, стр. 13-18., Anchorage, Alaska, 2000.

Документация

Luenberger Observer

Описание

Определение уравнений

Предположения

Ограничения

Порты

Вход

u - Управляющий вход вектор

y - Выходные данные системы вектор

Выход

xhat - Оценка состояния вектор

Параметры

State-space parameterization - Параметризация пространства состояний Discrete-time (по умолчанию) | Continuous-time

Discrete A matrix - Матрица за дискретное время 1 (по умолчанию) | действительный скаляр или матрица

Зависимости

Discrete B matrix - матрица B за дискретное время 1 (по умолчанию) | действительный скаляр или матрица

Зависимости

Discrete C matrix - матрица C за дискретное время 1 (по умолчанию) | действительный скаляр или матрица

Зависимости

Discrete D matrix - D-матрица за дискретное время 1 (по умолчанию) | действительный скаляр или матрица

Зависимости

Continuous A matrix - Матрица за непрерывное время 1 (по умолчанию) | действительный скаляр или матрица

Зависимости

Continuous B matrix - B матрица за непрерывное время 1 (по умолчанию) | действительный скаляр или матрица

Зависимости

Continuous C matrix - матрица C за непрерывное время 1 (по умолчанию) | действительный скаляр или матрица

Зависимости

Continuous D matrix - D-матрица за непрерывное время 1 (по умолчанию) | действительный скаляр или матрица

Зависимости

Observer design - Параметризация пространства состояний Desired eigenvalues (по умолчанию) | Observer gain

Зависимости

Observer gain - Коэффициент усиления наблюдателя 1 (по умолчанию) | действительный скаляр или матрица

Зависимости

Desired eigenvalues - Собственные значения наблюдателя 0 (по умолчанию) | вектор действительных чисел

Initial conditions - Начальные условия 0 (по умолчанию) | вектор действительных чисел с длиной, равной системному порядку

Discretization sample time - Дискретизация шага расчета 0,1 (по умолчанию) | положительное вещественное число

Зависимости

Sample time - Шаг расчета 0,1 (по умолчанию) | -1 или положительное вещественное число

Примеры моделей

Управление двигателем постоянного тока (обратная связь и наблюдатель)

Управление положением PMSM

Управление состоянием синхронной машины - Пространство

Ссылки

Расширенные возможности

Генерация кода C/C + + Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

См. также

Блоки

Simscape Electrical документация

Поддержка

`u` - Управляющий вход
вектор

`y` - Выходные данные системы
вектор

`xhat` - Оценка состояния
вектор

`State-space parameterization` - Параметризация пространства состояний
`Discrete-time` (по умолчанию) | `Continuous-time`

`Discrete A matrix` - Матрица за дискретное время
1 (по умолчанию) | действительный скаляр или матрица

`Discrete B matrix` - матрица B за дискретное время
1 (по умолчанию) | действительный скаляр или матрица

`Discrete C matrix` - матрица C за дискретное время
1 (по умолчанию) | действительный скаляр или матрица

`Discrete D matrix` - D-матрица за дискретное время
1 (по умолчанию) | действительный скаляр или матрица

`Continuous A matrix` - Матрица за непрерывное время
1 (по умолчанию) | действительный скаляр или матрица

`Continuous B matrix` - B матрица за непрерывное время
1 (по умолчанию) | действительный скаляр или матрица

`Continuous C matrix` - матрица C за непрерывное время
1 (по умолчанию) | действительный скаляр или матрица

`Continuous D matrix` - D-матрица за непрерывное время
1 (по умолчанию) | действительный скаляр или матрица

`Observer design` - Параметризация пространства состояний
`Desired eigenvalues` (по умолчанию) | `Observer gain`

`Observer gain` - Коэффициент усиления наблюдателя
1 (по умолчанию) | действительный скаляр или матрица

`Desired eigenvalues` - Собственные значения наблюдателя
0 (по умолчанию) | вектор действительных чисел

`Initial conditions` - Начальные условия
0 (по умолчанию) | вектор действительных чисел с длиной, равной системному порядку

`Discretization sample time` - Дискретизация шага расчета
0,1 (по умолчанию) | положительное вещественное число

`Sample time` - Шаг расчета
0,1 (по умолчанию) | -1 или положительное вещественное число

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®