Exponenta Banner

bearingFaultBands

Сгенерируйте полосы частот вокруг характерных частот отказа мяча или роликовых подшипников для спектральных редукций данных

Свернуть все на странице

Синтаксис

FB = bearingFaultBands(FR,NB,DB,DP,beta)
FB = bearingFaultBands(___,Name,Value)
[FB,info] = bearingFaultBands(___)
bearingFaultBands(___)

Описание

пример

FB = bearingFaultBands(FR,NB,DB,DP,beta) генерирует характерные полосы частот отказа FB роликового или шарового подшипника по его физическим параметрам. FR - скорость вращения вала или внутреннего кольца, NB количество мячей или роликов, DB - диаметр мяча или ролика, DP - диаметр тангажа и beta - угол контакта в степенях. Значения в FB имеют те же неявные модули, что и FR.

пример

FB = bearingFaultBands(___,Name,Value) позволяет вам задать дополнительные параметры, используя один или несколько аргументы пары "имя-значение".

пример

[FB,info] = bearingFaultBands(___) также возвращает структуру info содержит информацию о сгенерированных полосах частот отказа FB.

пример

bearingFaultBands(___) без выходных аргументов строит столбчатую диаграмму сгенерированных полос частот отказа FB.

Примеры

свернуть все

Открыть Live Script

В данном примере рассмотрим подшипник с диаметром тангажом 12 см с восемью элементами качения. Каждый элемент качения имеет диаметр 2 см. Внешнее кольцо остается стационарным, внутренне кольцо вращается со скоростью 25 Гц. Угол контакта элемента качения составляет 15 степени.

Используя вышеуказанные физические размерности подшипника, создайте полосы частот с помощью bearingFaultBands.

FR = 25;
NB = 8;
DB = 2;
DP = 12;
beta = 15;
FB = bearingFaultBands(FR,NB,DB,DP,beta)
FB = 4×2

   82.6512   85.1512
  114.8488  117.3488
   71.8062   74.3062
    9.2377   11.7377

FB возвращается как массив 4x2 с шириной полосы частот по умолчанию 10 процентов FR что составляет 2,5 Гц. Первый столбец в FB содержит значения F-W2, в то время как второй столбец содержит все значения F+W2 для каждой характеристики частоты дефекта.

Открыть Live Script

В данном примере рассмотрим подшипник микро-ролика с 11 роликами, где каждый ролик составляет 7,5 мм. Диаметр тангажа равен 34 мм, а угол контакта равен 0 степеням. Принимая скорость вала 1800 об/мин, создайте полосы частот для подшипника ролика. Задайте 'Domain'as' frequency', чтобы получить полосы частот FB в тех же модулях, что и FR.

FR = 1800;
NB = 11;
DB = 7.5;
DP = 34;
beta = 0;
[FB1,info1] = bearingFaultBands(FR,NB,DB,DP,beta,'Domain','frequency')
FB1 = 4×2
104 ×

    0.7626    0.7806
    1.1994    1.2174
    0.3791    0.3971
    0.0611    0.0791


info1 = struct with fields:
        Centers: [7.7162e+03 1.2084e+04 3.8815e+03 701.4706]
         Labels: ["1Fo"    "1Fi"    "1Fb"    "1Fc"]
    FaultGroups: [1 2 3 4]

Теперь включите боковые полосы для внутренней обоймы и частоты дефекта элемента качения, используя 'Sidebands'пара "имя-значение".

[FB2,info2] = bearingFaultBands(FR,NB,DB,DP,beta,'Domain','order','Sidebands',0:1)
FB2 = 8×2

    4.2368    4.3368
    5.6632    5.7632
    6.6632    6.7632
    7.6632    7.7632
    1.7167    1.8167
    2.1064    2.2064
    2.4961    2.5961
    0.3397    0.4397


info2 = struct with fields:
        Centers: [4.2868 5.7132 6.7132 7.7132 1.7667 2.1564 2.5461 0.3897]
         Labels: [1x8 string]
    FaultGroups: [1 2 2 2 3 3 3 4]

Можно использовать сгенерированные полосы отказов FB для извлечения спектральных метрик с помощью faultBandMetrics команда.

Открыть Live Script

В данном примере рассмотрим поврежденный подшипник с диаметром тангажом 12 см с восемью элементами качения. Каждый элемент качения имеет диаметр 2 см. Внешнее кольцо остается стационарным, внутренне кольцо вращается со скоростью 25 Гц. Угол контакта элемента качения составляет 15 степени.

При вышеуказанных физических размерностях подшипника визуализируйте полосы частот отказа с помощью bearingFaultBands.

FR = 25;
NB = 8;
DB = 2;
DP = 12;
beta = 15;
bearingFaultBands(FR,NB,DB,DP,beta)

Figure contains an axes. The axes with title Fault Frequency Bands contains 8 objects of type patch, text.

На графике наблюдайте следующие частоты вибрации подшипников:

  • Частота дефектов клетки, Fc при 10,5 Гц.

  • Частота дефектов мяча, Fb при 73 Гц.

  • Частота дефектов внешнего кольца, Fo при 83,9 Гц.

  • Частота дефектов внутренней расы, Fi при 116,1 Гц.

Открыть Live Script

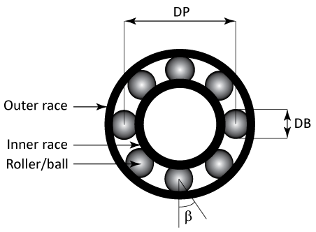
В данном примере рассмотрим мяч подшипника с тангажом диаметром 12 см с 10 элементами качения. Каждый элемент качения имеет диаметр 0,5 см. Внешнее кольцо остается стационарным, внутренне кольцо вращается со скоростью 25 Гц. Угол контакта мяча составляет 0 степени. Набор данных bearingData.mat содержит степень (PSD) спектральную плотность и ее соответствующие частотные данные для сигнала вибрации подшипника в таблице.

Сначала создайте полосы частот подшипника, включая первые 3 боковые полосы, используя физические характеристики шарикового подшипника.

FR = 25;
NB = 10;
DB = 0.5;
DP = 12;
beta = 0;
FB = bearingFaultBands(FR,NB,DB,DP,beta,'Sidebands',1:3)
FB = 14×2

  118.5417  121.0417
   53.9583   56.4583
   78.9583   81.4583
  103.9583  106.4583
  153.9583  156.4583
  178.9583  181.4583
  203.9583  206.4583
  262.2917  264.7917
  274.2708  276.7708
  286.2500  288.7500
      ⋮

FB массив 14x2, который включает первичные частоты и их боковые полосы.

Загрузите данные PSD. bearingData.mat содержит таблицу X где PSD содержится в первом столбце, а частотная сетка - во втором столбце, как массивы ячеек соответственно.

load('bearingData.mat','X')
X
X=1×2 table
          Var1                Var2      
    ________________    ________________

    {12001x1 double}    {12001x1 double}

Вычислите спектральные метрики, используя данные PSD в таблице X и полосы частот в FB.

spectralMetrics = faultBandMetrics(X,FB)
spectralMetrics=1×43 table
    PeakAmplitude1    PeakFrequency1    BandPower1    PeakAmplitude2    PeakFrequency2    BandPower2    PeakAmplitude3    PeakFrequency3    BandPower3    PeakAmplitude4    PeakFrequency4    BandPower4    PeakAmplitude5    PeakFrequency5    BandPower5    PeakAmplitude6    PeakFrequency6    BandPower6    PeakAmplitude7    PeakFrequency7    BandPower7    PeakAmplitude8    PeakFrequency8    BandPower8    PeakAmplitude9    PeakFrequency9    BandPower9    PeakAmplitude10    PeakFrequency10    BandPower10    PeakAmplitude11    PeakFrequency11    BandPower11    PeakAmplitude12    PeakFrequency12    BandPower12    PeakAmplitude13    PeakFrequency13    BandPower13    PeakAmplitude14    PeakFrequency14    BandPower14    TotalBandPower
    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    ______________

         121               121            314.43          56.438            56.438          144.95          81.438            81.438          210.57          106.44            106.44          276.2           156.44            156.44          407.45          181.44            181.44          473.07          206.44            206.44          538.7           264.75            264.75          691.77          276.75            276.75          723.27          288.69             288.69           754.61           312.69             312.69           817.61           324.62             324.62           848.94           336.62             336.62           880.44           13.188             13.188           31.418           7113.4

spectralMetrics - таблица 1x43 с пиковой амплитудой, пиковой частотой и мощностью полосы, рассчитанных для каждой частотной области значений в FB. Последний столбец в spectralMetrics - общая мощность полосы, вычисленная по всем частотам 14 в FB.

Входные параметры

свернуть все

Скорость вращения вала или внутреннего кольца, заданная как положительная скалярная величина. FR - основная частота, вокруг которой bearingFaultBands генерирует полосы частот отказа. Задайте FR либо в Герце, либо обороты в минуту.

Количество мячей или роликов в подшипнике, заданное в виде положительного целого числа.

Диаметр мяча или ролика, заданный как положительное целое число.

Тангаж диаметр подшипника, заданный как положительная скалярная величина. DP - диаметр окружности, которую центр мяча или ролика перемещает во время вращения подшипника.

Угол контакта в степени между плоскостью, перпендикулярной оси мяча или ролика, и линией, соединяющей две канавки, заданный как положительная скалярная величина.

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

Пример: ...,'Harmonics',[1,3,5]

Гармоники основной частоты, которая будет включена, задаются как разделенная разделенными запятой парами, состоящая из 'Harmonics'и вектор положительных целых чисел. Значение по умолчанию является 1. Задайте 'Harmonics'когда вы хотите создать полосы частот с больше гармоник основной частоты.

Боковые полосы вокруг основной частоты и ее гармоник, которые будут включены, заданы как разделенная разделенными запятой парами, состоящая из 'Sidebands'и вектор неотрицательных целых чисел. Значение по умолчанию 0. Задайте 'Sidebands'когда вы хотите создать полосы частот с боковыми полосами вокруг основной частоты и ее гармоник.

Ширина полос частот с центром на номинальных частотах отказа, заданная как разделенная разделенными запятой парами, состоящая из 'Width'и положительный скаляр. Значение по умолчанию является 10 процентами от основной частоты. Избегайте задавать 'Width'с большим значением, чтобы полосы отказов не перекрывались.

Модули частот полосы отказов, заданные как разделенная разделенными запятой парами, состоящая из 'Domain'и любой из них 'frequency' или 'order'. Выберите:

  • 'frequency' если хотите FB будет возвращено в тех же модулях, что и FR.

  • 'order' если хотите FB будет возвращено как количество вращений относительно вращения внутреннего кольца, FR.

Выходные аргументы

свернуть все

Полосы частот отказа, возвращенные как Nx2 массив, где N - количество частот отказа. FB возвращается в тех же модулях, что и FR, в герце или порядках в зависимости от значения 'Domain'. Используйте сгенерированные полосы частот отказа, чтобы извлечь спектральные метрики, используя faultBandMetrics. Сгенерированные полосы отказов, [F−W2, F+W2], центрированы в:

  • Частота дефектов внешнего кольца, Fo и его гармоники

  • Частота дефектов внутренней расы, Fi, его гармоники и боковые полосы в FR

  • Частота дефектов элемента качения ( мяча), Fbего гармоника и боковые полосы в Fc

  • Частота дефектов клетки (train), Fc и его гармоники

Значение W - ширина полос частот, которую можно задать с помощью 'Width'пара "имя-значение". Для получения дополнительной информации о несущих частотах см. Алгоритмы.

Информация о полосах частот отказа в FB, возвращенный как структура со следующими полями:

  • Centers - Частоты центрального отказа

  • Labels - Метки, описывающие каждую частоту

  • FaultGroups - Номера групп отказов, идентифицирующие соответствующие частоты отказов

Алгоритмы

bearingFaultBands вычисляет различные характеристики несущих частот следующим образом:

  • Частота дефектов внешнего кольца, Fo=NB2FR(1−DBDPпотому что(β))

  • Частота дефектов внутренней расы, Fi=NB2FR(1+DBDPпотому что(β))

  • Частота дефектов элемента качения ( мяча), Fb=DP2DBFR(1−[DBDPпотому что(β)]2)

  • Частота дефектов клетки (train),Fc=FR2(1−DBDPпотому что(β))

Ссылки

[1] Chandravanshi, M & Poddar, Surojit. «Мяч поломок шарового подшипника с использованием параметров вибрации». Международный журнал инженерных исследований и технологий. 2. 2013.

[2] Singh, Sukhjeet & Kumar, Amit & Kumar, Navin. «Анализ сигнатур тока двигателя для обнаружения поломок подшипника в механических системах». Методика материаловедения. 6. 171–177. 10.1016/j.mspro.2014.07.021. 2014.

[3] Roque, Antonio & Silva, Tiago & Calado, Jo, & Dias, J. «Подход к диагностике отказа подшипников качения». Сделки WSEAS по системам и управлению. 4. 2009.

См. также

| |

Введенный в R2019b

Документация Predictive Maintenance Toolbox

Поддержка