Линеаризация является линейным приближением нелинейной системы, которая действительна в небольшой области вокруг рабочей точки.
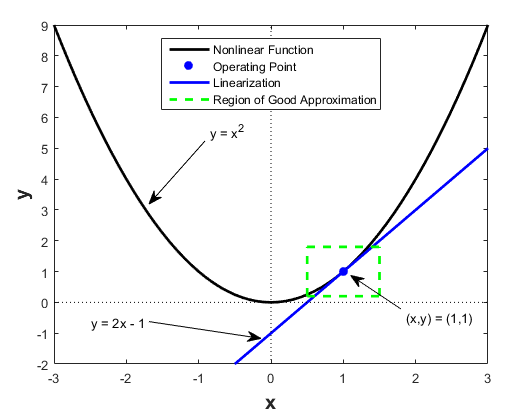
Для примера предположим, что нелинейная функция является . Линеаризация этой нелинейной функции о рабочей точке x = 1, y = 1 приводит к линейной функции .
Рядом с рабочей точкой, является хорошим приближением к . Вдали от рабочей точки приближение плохое.
Следующий рисунок показывает возможную область хорошего приближения для линеаризации . Фактическая область валидности зависит от нелинейной модели.
Распространяя концепцию линеаризации на динамические системы, можно записать нелинейные дифференциальные уравнения непрерывного времени в этой форме:
В этих уравнениях x (t) представляет состояния системы, u (t) представляет входы системы, и y (t) представляет выходы системы.
Линеаризированная модель этой системы действительна в небольшой области вокруг рабочей точки t = t0, x (t0) = x0, u (t0) = u0 и y (t0) = g (x0, u0, t0) = y0.
Чтобы представлять линеаризированную модель, задайте новые переменные с центром вокруг рабочей точки:
Линеаризовавшая модель с точки зрения δx, δu, и δy действительна, когда значения этих переменных маленькие:
Линеаризация полезна в анализе модели и системе управления.
Точная линеаризация заданного нелинейного Simulink® модель производит линейное пространство состояний, передаточную функцию или нули , полюса и усиления, которые можно использовать для:
Постройте график отклика Bode модели Simulink.
Оцените запасы устойчивости цикла путем вычисления отклика без разомкнутого контура.
Анализируйте и сравните реакцию объекта вблизи различных рабочих точек.
Проектируйте линейный контроллер
Для анализа и проекта классических систем управления требуются линейные, инвариантные по времени модели. Simulink Control Design™ автоматически линеаризирует объект, когда вы настраиваете компенсатор. См. «Выбор подхода к проектированию систем управления».
Анализ устойчивости замкнутого контура.
Измерьте размер резонансов в частотной характеристики путем вычисления линейной модели с обратной связью для системы управления.
Сгенерируйте контроллеры с пониженной чувствительностью к изменениям параметров и ошибкам моделирования.
Можно использовать программное обеспечение Simulink Control Design, чтобы линеаризировать модели Simulink в непрерывном времени, дискретном времени или многомерные. Получившаяся линейная инвариантная по времени модель находится в форме пространства состояний.
По умолчанию Simulink Control Design линеаризирует модели с помощью блочного подхода. Этот блочно-блочный подход индивидуально линеаризирует каждый блок в вашей модели Simulink и объединяет результаты, чтобы создать линеаризацию указанной системы.
Можно также линеаризировать систему с помощью числовых возмущений полной модели, где программа вычисляет линеаризацию полной модели, возмущая значения входов и состояний корневого уровня. Для каждого входа и состояния программное обеспечение возмущает модель на небольшую величину и вычисляет линейную модель на основе реакции модели на эти возмущения. Можно возмущать модель, используя либо прямые различия, либо центральные различия.
Подход блочной линеаризации имеет несколько преимуществ для полномодельной числовой возмущения:
Большинство блоков Simulink имеют предварительно запрограммированную линеаризацию, которая обеспечивает точную линеаризацию блока.
Можно использовать точки линейного анализа, чтобы задать фрагмент модели для линеаризации.
Можно сконфигурировать блоки, чтобы использовать пользовательские линеаризации, не влияя на симуляцию модели.
Структурно неминимальные состояния автоматически удаляются.
Можно задать линеаризации, которые включают неопределенность (требует Robust Control Toolbox™ программного обеспечения).
Вы можете получить подробную диагностическую информацию.
При линеаризации многоскоростных моделей можно использовать различные методы преобразования скорости. Численное возмущение полной модели может использовать только нуль преобразования скорости удержания порядка.
Точная линеаризация поддерживает большинство блоков Simulink.
Однако блоки Simulink с сильными разрывами или основанной на событиях динамикой линеаризируются (правильно) к нулю или большому (бесконечному) усилению. Модели, которые включают основанное на событиях или прерывистое поведение, требуют специальной обработки программным обеспечением Simulink Control Design. Такое основанное на событиях или прерывистое поведение может происходить из таких блоков, как:
Блоки из библиотеки прерываний
Stateflow® чарты
Триггируемые подсистемы
Сигналы модуляции ширины импульса (PWM)
Для большинства приложений состояния в вашей модели Simulink должны быть в установившемся состоянии. В противном случае ваша линейная модель действительна только в течение небольшого временного интервала.
Выбор правой рабочей точки для линеаризации очень важен для получения точной линейной модели. Линейная модель является приближением нелинейной модели, которая действительна только около рабочей точки, в которой вы линеаризируете модель.
Несмотря на то, что вы задаете, какие блоки Simulink нужно линеаризировать, все блоки в модели влияют на рабочую точку.
Нелинейная модель может иметь два очень разных линейных приближения, когда вы линеаризируетесь относительно различных рабочих точек.
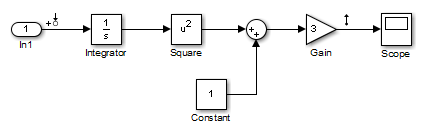
Результат линеаризации для этой модели показан следующим, с начальным условием для интегрирования x 0 = 0.

В этой таблице представлены различные результаты линеаризации для двух различных рабочих точек.
| Рабочая точка | Результат линеаризации |
|---|---|
Начальное условие = 5, Состояние x1 = 5 | 30/с |
Начальное условие = 0, Состояние x1 = 0 | 0 |
Можно линеаризировать модель Simulink в трех различных типах рабочих точек:
Обрезанная рабочая точка - линеаризация в обрезанной рабочей точке
Симуляционный снимок - Линеаризация на симуляционном снимке
Срабатывающее событие симуляции - линеаризация при срабатывании событий симуляции