Exponenta Banner

linkage

Агломеративное иерархическое дерево кластеров

Свернуть все на странице

Синтаксис

Z = linkage(X)
Z = linkage(X,method)
Z = linkage(X,method,metric)
Z = linkage(X,method,metric,'savememory',value)
Z = linkage(X,method,pdist_inputs)
Z = linkage(y)
Z = linkage(y,method)

Описание

Z = linkage(X) возвращает матрицу Z который кодирует дерево, содержащее иерархические кластеры строк матрицы входных данных X.

пример

Z = linkage(X,method) создает дерево с помощью заданной method, который описывает, как измерить расстояние между кластерами. Для получения дополнительной информации см. Редактирования»

пример

Z = linkage(X,method,metric) выполняет кластеризацию путем передачи metric в pdist функция, которая вычисляет расстояние между строками X.

пример

Z = linkage(X,method,metric,'savememory',value) использует алгоритм сохранения памяти при value является 'on', и использует стандартный алгоритм, когда value является 'off'.

пример

Z = linkage(X,method,pdist_inputs) проходит pdist_inputs в pdist функция, которая вычисляет расстояние между строками X. The pdist_inputs аргумент состоит из 'seuclidean', 'minkowski', или 'mahalanobis' метрика и дополнительная опция метрики расстояния.

Z = linkage(y) использует представление вектора y матрицы расстояний. y вычисляется либо pdist или является более общей матрицей расхождения, соответствующей выходу pdist.

пример

Z = linkage(y,method) создает дерево с помощью заданной method, который описывает, как измерить расстояние между кластерами.

Примеры

свернуть все

Открыть Live Script

Случайным образом сгенерируйте выборочные данные с 20 000 наблюдений.

rng('default') % For reproducibility
X = rand(20000,3);

Создайте иерархическое дерево кластеров с помощью ward СПОСОБ редактирования. В этом случае 'SaveMemory' опция clusterdata функция установлена в 'on' по умолчанию. В целом задайте лучшее значение для 'SaveMemory' на основе размерностей X и доступную память.

Z = linkage(X,'ward');

Объедините данные в максимум четыре группы и постройте график результата.

c = cluster(Z,'Maxclust',4);
scatter3(X(:,1),X(:,2),X(:,3),10,c)

Figure contains an axes. The axes contains an object of type scatter.

cluster определяет четыре группы в данных.

Открыть Live Script

Найти максимум три кластера в fisheriris набор данных и сравнение кластерных назначений цветов с их известной классификацией.

Загрузите выборочные данные.

load fisheriris

Создайте иерархическое дерево кластеров с помощью 'average' метод и 'chebychev' метрический.

Z = linkage(meas,'average','chebychev');

Найдите в данных не более трех кластеров.

T = cluster(Z,'maxclust',3);

Создайте дендрограммный график Z. Чтобы увидеть три кластера, используйте 'ColorThreshold' с отсечкой на полпути между третьим - с последнего и вторым - с последнего - редактированиями.

cutoff = median([Z(end-2,3) Z(end-1,3)]);
dendrogram(Z,'ColorThreshold',cutoff)

Figure contains an axes. The axes contains 29 objects of type line.

Отображение последних двух строк Z чтобы увидеть, как три кластера объединяются в один. linkage объединяет 293-й (синий) кластер с 297-м (красным) кластером, образуя 298-й кластер со редактированием 1.7583. linkage затем объединяет 296-й (зеленый) кластер с 298-м кластером.

lastTwo = Z(end-1:end,:)
lastTwo = 2×3

  293.0000  297.0000    1.7583
  296.0000  298.0000    3.4445

Посмотрите, как назначения кластеров соответствуют трем видам. Например, один из кластеров содержит 50 цветы второго вида и 40 цветы третьего вида.

crosstab(T,species)
ans = 3×3

     0     0    10
     0    50    40
    50     0     0
Открыть Live Script

Загрузите examgrades набор данных.

load examgrades

Создайте иерархическое дерево с помощью linkage. Используйте 'single' метод и метрика Минковского с показателем 3.

Z = linkage(grades,'single',{'minkowski',3});

Наблюдайте 25-й шаг кластеризации.

Z(25,:)
ans = 1×3

   86.0000  137.0000    4.5307

linkage объединяет 86-е наблюдение и 137-е кластер для формирования кластера индексов 120+25=145, где 120 - общее количество наблюдений в grades и 25 - номер строки в Z. Самое короткое расстояние между 86-м наблюдением и любой из точек 137-ого кластера 4.5307.

Открыть Live Script

Создайте агломеративное иерархическое дерево кластеров с помощью матрицы различий.

Возьмем матрицу различий X и преобразуйте его в вектор форму, которая linkage принимает при помощи squareform.

X = [0 1 2 3; 1 0 4 5; 2 4 0 6; 3 5 6 0];
y = squareform(X);

Создайте дерево кластеров с помощью linkage с 'complete' способ вычисления расстояния между кластерами. Первые два столбца Z показать, как linkage объединяет кластеры. Третий столбец Z задает расстояние между кластерами.

Z = linkage(y,'complete')
Z = 3×3

     1     2     1
     3     5     4
     4     6     6

Создайте дендрограммный график Z. Ось X соответствует листовым узлам дерева, а ось Y соответствует расстояниям редактирования между кластерами.

dendrogram(Z)

Figure contains an axes. The axes contains 3 objects of type line.

Входные параметры

свернуть все

Входные данные, заданные как числовая матрица с двумя или более строками. Строки представляют наблюдения, а столбцы - категории или размерности.

Типы данных: single | double

Алгоритм вычисления расстояния между кластерами, заданный как одно из значений в этой таблице.

МетодОписание
'average'

Невзвешенное среднее расстояние (UPGMA)

'centroid'

Расстояние центроида (UPGMC), соответствующее только евклидовым расстояниям

'complete'

Самое дальнее расстояние

'median'

Взвешенное расстояние по центру масс (WPGMC), соответствующее только евклидовым расстояниям

'single'

Кратчайшее расстояние

'ward'

Внутреннее квадратное расстояние (алгоритм минимального отклонения), соответствующее только евклидовым расстояниям

'weighted'

Средневзвешенное расстояние (WPGMA)

Для получения дополнительной информации об этих методах смотрите редактирования.

Метрика расстояния, заданная как любая метрика, принятая pdist функция. Эти метрики описаны в следующей таблице.

ЗначениеОписание
'euclidean'

Евклидово расстояние (по умолчанию).

'squaredeuclidean'

Квадратное Евклидово расстояние. (Эта опция предусмотрена только для эффективности. Это не удовлетворяет неравенству треугольника.)

'seuclidean'

Стандартизированное евклидово расстояние. Каждое различие координат между наблюдениями масштабируется путем деления на соответствующий элемент стандартного отклонения, S = std(X,'omitnan'). Использование DistParameter чтобы задать другое значение для S.

'mahalanobis'

Расстояние Махаланобиса с помощью выборочной ковариации X, C = cov(X,'omitrows'). Использование DistParameter чтобы задать другое значение для C, где матрица C симметричен и положительно определен.

'cityblock'

Расстояние между блоками.

'minkowski'

Расстояние Минковского. Экспонента по умолчанию является 2. Использование DistParameter чтобы задать другую экспоненту P, где P - положительная скалярная величина значение экспоненты.

'chebychev'

Расстояние Чебычева (максимальное различие координат).

'cosine'

Один минус косинус включенного угла между точками (рассматривается как векторы).

'correlation'

Один минус корреляция выборки между точками (рассматривается как последовательности значений).

'hamming'

Расстояние Хемминга, которое является процентом различий координат.

'jaccard'

Один минус коэффициент Жаккара, который является процентом ненулевых координат, которые различаются.

'spearman'

Один минус выборки корреляции ранга Спирмана между наблюдениями (рассматриваются как последовательности значений).

distfun

Пользовательский указатель на функцию расстояния. Функция расстояния имеет вид

function D2 = distfun(ZI,ZJ)
% calculation of distance
...
где

  • ZI является 1-by- n вектор, содержащий одно наблюдение.

  • ZJ является m2-by- n матрица, содержащая несколько наблюдений. distfun необходимо принять матрицу ZJ с произвольным количеством наблюдений.

  • D2 является m2-by- 1 вектор расстояний, и D2(k) - расстояние между наблюдениями ZI и ZJ(k,:).

Если ваши данные не разрежены, вы обычно можете вычислить расстояние быстрее, используя встроенное расстояние вместо указателя на функцию.

Для получения дополнительной информации см. «Метрики расстояния».

Использование pdist_inputs вместо metric чтобы задать дополнительный входной параметр DistParameter из pdist для 'seuclidean', 'minkowski', или 'mahalanobis'.

Типы данных: char | string | function_handle

Метрика расстояния и опция метрики расстояния, заданная как массив ячеек разделенной разделенными запятой парами, состоящей из двух входных параметров Distance и DistParameter функции pdist. Этот аргумент действителен только для определения 'seuclidean', 'minkowski', или 'mahalanobis'.

Пример: {'minkowski',5}

Типы данных: cell

Флаг для 'savememory' опция, заданная как 'on' или 'off'. The 'on' причины настройки linkage чтобы создать кластеры, не вычисляя матрицу расстояний. The 'on' установка доступна только тогда, когда method является 'centroid', 'median', или 'ward' и metric является 'euclidean'.

Когда value является 'on', linkage время выполнения пропорционально количеству размерностей (количеству столбцов X). Когда value является 'off', linkage требование к памяти пропорционально N2, где N количество наблюдений. Лучшая (наименьшая) настройка для value зависит от размерностей задачи, количества наблюдений и доступной памяти. Значение по умолчанию value Установка является грубым приближением оптимальной настройки.

Значение по умолчанию является 'on' когда X имеет 20 столбцов или меньше, или компьютер не имеет достаточной памяти для хранения матрицы расстояний. В противном случае значение по умолчанию является 'off'.

Пример: 'savememory','on'

Расстояния, заданные как числовой вектор с таким же форматом, как и выход pdist функция:

  • Вектор-строка длины m (m - 1 )/2, соответствующий парам наблюдений в матрице с m строками

  • Расстояния, расположенные в порядок (2,1) , (3,1),..., (m, 1), (3,2),..., (m, 2),..., (m, m - 1)

y может быть более общей матрицей расхождения, соответствующей выходному формату pdist.

Типы данных: single | double

Выходные аргументы

свернуть все

Агломеративное иерархическое дерево кластера, возвращенное в виде числовой матрицы. Z является (m - 1) -на-3 матрицей, где m - количество наблюдений в исходных данных. Столбцы 1 и 2 Z содержат индексы кластера, связанные парами, для формирования двоичного дерева. Узлы листа пронумерованы от 1 до m. Листовые узлы являются синглтонными кластерами, из которых построены все более высокие кластеры. Каждый вновь сформированный кластер, соответствующий Z(I,:) строк, присвоен индекс m + I. Значения Z(I,1) и Z(I,2) содержат индексы двух кластеров компонентов, образующих кластер m + I. m - 1 более высокие кластеры соответствуют внутренним узлам дерева кластеризации. Z(I,3) содержит редактирование расстояние между двумя кластерами, объединенными в строку Z(I,:).

Например, рассмотрите создание дерева с 30 начальными узлами. Предположим, что кластер 5 и кластер 7 объединяются на этапе 12 и что расстояние между ними на этом этапе составляет 1,5. Затем Z(12,:) является [5 7 1.5]. Новообразованный кластер имеет индекс 12 + 30 = 42. Если кластер 42 появляется в более поздней строке, то функция объединяет кластер, созданный на этапе 12, в больший кластер.

Типы данных: single | double

Подробнее о

свернуть все

Редактирования

Редактирование - это расстояние между двумя кластерами.

Следующее обозначение описывает редактирования, используемые различными методами:

  • Кластер r формируется из кластеров p и q.

  • n r - это количество объектов в r кластера.

  • x ri является i-м объектом в r кластеров.

  • Одно редактирование, также называемое ближайшим соседом, использует наименьшее расстояние между объектами в двух кластерах.

    d(r,s)=min(dist(xri,xsj)),i∈(i,...,nr),j∈(1,...,ns)

  • Полное редактирование, также называемое самым дальним соседом, использует самое большое расстояние между объектами в двух кластерах.

    d(r,s)=max(dist(xri,xsj)),i∈(1,...,nr),j∈(1,...,ns)

  • Среднее редактирование использует среднее расстояние между всеми парами объектов в любых двух кластерах.

    d(r,s)=1nrns∑i=1nr∑j=1nsdist(xri,xsj)

  • Центроидное редактирование использует евклидово расстояние между центроидами двух кластеров.

    d(r,s)=‖x¯r−x¯s‖2,

    где

    x¯r=1nr∑i=1nrxri

  • Срединное редактирование использует евклидово расстояние между взвешенными центроидами двух кластеров.

    d(r,s)=‖x˜r−x˜s‖2,

    где x˜r и x˜s являются взвешенными центроидами для кластеров r и s. Если r кластера была создана путем объединения кластеров p и q, x˜r определяется рекурсивно как

    x˜r=12(x˜p+x˜q)

  • Редактирование Уорда использует инкрементальную сумму квадратов, то есть увеличение общей суммы квадратов внутри кластера в результате соединения двух кластеров. Внутри кластера сумма квадратов определяется как сумма квадратов расстояний между всеми объектами в кластере и центроидом кластера. Сумма метрики квадратов эквивалентна следующей метрике расстояния d (r, s), которая является формулойlinkage использует.

    d(r,s)=2nrns(nr+ns)‖x¯r−x¯s‖2,

    где

    • ‖‖2 - евклидово расстояние.

    • x¯r и x¯s являются центроидами кластеров r и s.

    • nr и ns являются количеством элементов в кластерах r и s.

    В некоторых ссылках редактирование Уорда не использует множитель 2 nrns. linkage функция использует этот коэффициент так, что расстояние между двумя синглтонными кластерами совпадает с евклидовым расстоянием.

  • Взвешенное среднее редактирование использует рекурсивное определение для расстояния между двумя кластерами. Если r кластера была создана путем объединения кластеров p и q, расстояние между r и другим s кластера определяется как среднее расстояние между p и s и расстояние между q и s.

    d(r,s)=(d(p,s)+d(q,s))2

Совет

  • Вычислительные linkage(y) может быть медленным, когда y является вектор представлением матрицы расстояний. Для 'centroid', 'median', и 'ward' методы, linkage проверяет, y ли - евклидово расстояние. Избегайте этой длительной проверки, передавая X вместо y.

  • The 'centroid' и 'median' методы могут создать дерево кластеров, которое не является монотонным. Этот результат происходит, когда расстояние от объединения двух кластеров, r и s, до третьего кластера меньше, чем расстояние между r и s. В этом случае в дендрограмме, нарисованной с ориентацией по умолчанию, путь от листа к корневому узлу делает несколько шагов вниз. Чтобы избежать этого результата, используйте другой метод. Этот рисунок показывает немонотонное дерево кластеров.

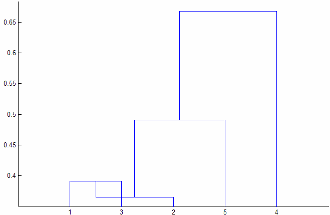
    В этом случае кластер 1 и кластер 3 соединяются в новый кластер, и расстояние между этим новым кластером и кластером 2 меньше, чем расстояние между кластером 1 и кластером 3. Результатом является немонотонное дерево.

  • Можно предоставить выход Z к другим функциям, включая dendrogram для отображения дерева, cluster для назначения точек кластерам, inconsistent вычислить несогласованные измерения, и cophenet для вычисления кофенетического коэффициента корреляции.

См. также

| | | | | | | |

Темы

Представлено до R2006a

Statistics and Machine Learning Toolbox документация

Поддержка