Документация

Загрузите выборочные данные.

Загрузите выборочные данные. Данные включают рейтинги по 9 различным показателям качества жизни в 329 городах США. Это климат, жилье, здравоохранение, преступность, транспорт, образование, искусство, отдых и экономика. Для каждой категории выше рейтинг лучше. Например, более высокий рейтинг преступности означает более низкий уровень преступности.

Отобразите categories переменная.

load cities
categories

categories =
   climate       
   housing       
   health        
   crime         
   transportation
   education     
   arts          
   recreation    
   economics   

Всего, cities набор данных содержит три переменные:

Постройте графики данных.

Сделайте прямоугольный график, чтобы просмотреть распределение ratings данные.

figure()
boxplot(ratings,'Orientation','horizontal','Labels',categories)

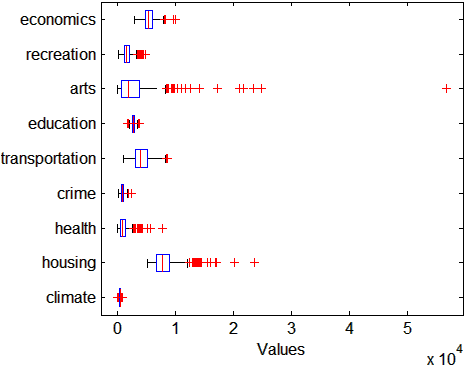
В рейтингах искусства и жилищного строительства существует большая изменчивость, чем в рейтингах преступности и климата.

Проверяйте парную корреляцию.

Проверяйте парную корреляцию между переменными.

C = corr(ratings,ratings);

Корреляция среди некоторых переменных достигает 0,85. Анализ основных компонентов создает независимые новые переменные, которые являются линейными комбинациями исходных переменных.

Вычислите основные компоненты.

Когда все переменные находятся в одном модуле, целесообразно вычислить основные компоненты для необработанных данных. Когда переменные находятся в разных модулях измерения или различие в отклонении различных столбцов существенно (как в этом случае), масштабирование данных или использование весов часто является предпочтительным.

Выполните анализ основного компонента, используя обратные отклонения рейтингов в качестве весов.

w = 1./var(ratings);
[wcoeff,score,latent,tsquared,explained] = pca(ratings,...
'VariableWeights',w);

Или эквивалентно:

[wcoeff,score,latent,tsquared,explained] = pca(ratings,...
'VariableWeights','variance');

В следующих разделах поясняются пять выходов pca.

Коэффициенты компонента.

Первый выход, wcoeff, содержит коэффициенты основных компонентов.

Первые три вектора коэффициентов главных компонентов:

c3 = wcoeff(:,1:3)

c3 = wcoeff(:,1:3)
c3 =

   1.0e+03 *

    0.0249   -0.0263   -0.0834
    0.8504   -0.5978   -0.4965
    0.4616    0.3004   -0.0073
    0.1005   -0.1269    0.0661
    0.5096    0.2606    0.2124
    0.0883    0.1551    0.0737
    2.1496    0.9043   -0.1229
    0.2649   -0.3106   -0.0411
    0.1469   -0.5111    0.6586

Эти коэффициенты взвешены, поэтому матрица коэффициентов не ортонормальна.

Коэффициенты преобразования.

Преобразуйте коэффициенты так, чтобы они были ортонормальными.

 coefforth = inv(diag(std(ratings)))*wcoeff;

Обратите внимание, что если вы используете вектор весов, w, при проведении pca, затем

 coefforth = diag(sqrt(w))*wcoeff;

Проверяющие коэффициенты ортонормальны.

Преобразованные коэффициенты теперь ортонормальны.

I = coefforth'*coefforth;
I(1:3,1:3)

ans =
    1.0000   -0.0000   -0.0000
   -0.0000    1.0000   -0.0000
   -0.0000   -0.0000    1.0000

Счета компонентов.

Второй выход, score, содержит координаты исходных данных в новой системе координат, заданные основными компонентами. The score матрица имеет тот же размер, что и матрица входных данных. Можно также получить счета компонентов с помощью ортонормальных коэффициентов и стандартизированных рейтингов следующим образом.

cscores = zscore(ratings)*coefforth;

cscores и score являются идентичными матрицами.

Постройте счета компонентов.

Создать график первых двух столбцов score.

figure()
plot(score(:,1),score(:,2),'+')
xlabel('1st Principal Component')
ylabel('2nd Principal Component')

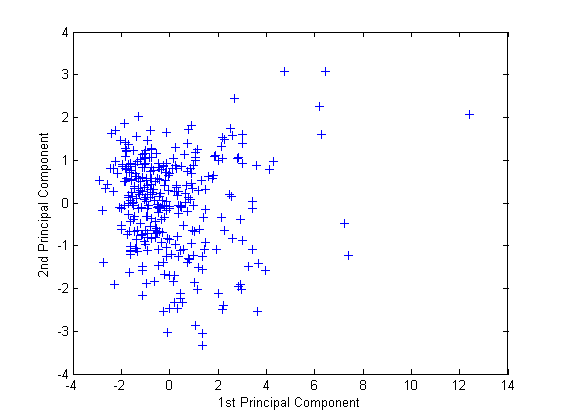
Этот график показывает центрированные и масштабированные данные рейтингов, проецируемые на первые два основных компонента. pca вычисляет счета, имеющие среднее нуль.

Исследуйте график в интерактивном режиме.

Обратите внимание на периферийные точки в правой половине графика. Можно графически идентифицировать эти точки следующим образом.

gname

Наведите курсор на график и щелкните один раз рядом с крайними правыми семью точками. Это помечает точки по номерам их строк как на следующем рисунке.

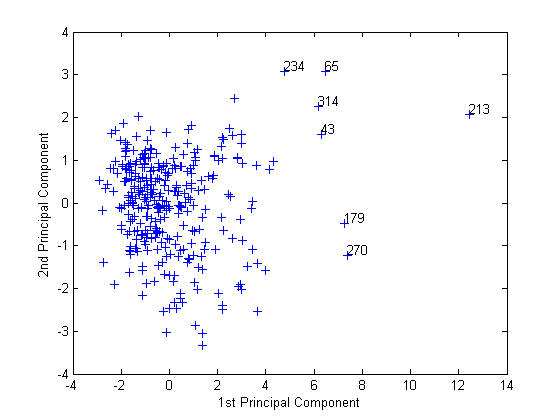
После маркировки точек нажмите Return.

Извлеките имена наблюдений.

Создайте индексную переменную, содержащую номера строк всех выбранных вами городов, и получите имена городов.

metro = [43 65 179 213 234 270 314];
names(metro,:)

ans =
   Boston, MA                  
   Chicago, IL                 
   Los Angeles, Long Beach, CA 
   New York, NY                
   Philadelphia, PA-NJ         
   San Francisco, CA           
   Washington, DC-MD-VA

Эти маркированные города являются одними из крупнейших населенных пунктов в Соединенных Штатах, и они кажутся более экстремальными, чем остальная часть данных.

Отклонения компонентов.

Третий выход, latent, является вектором, содержащим отклонение, объясненную соответствующим основным компонентом. Каждый столбец score имеет отклонение выборки, равную соответствующей строке latent.

latent

latent =

    3.4083
    1.2140
    1.1415
    0.9209
    0.7533
    0.6306
    0.4930
    0.3180
    0.1204

Объяснено процентное отклонение.

Пятый выход, explained, - вектор, содержащий процентное отклонение, объясненную соответствующим основным компонентом.

explained

explained =

   37.8699
   13.4886
   12.6831
   10.2324
    8.3698
    7.0062
    5.4783
    3.5338
    1.3378

Создайте график scree.

Постройте график переменности процента, объясняемый каждым основным компонентом.

figure()
pareto(explained)
xlabel('Principal Component')
ylabel('Variance Explained (%)')

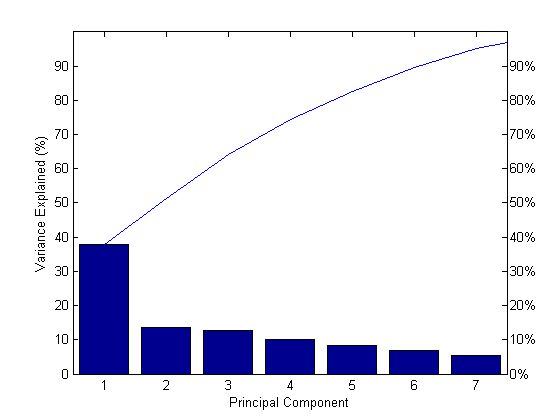
Этот график scree показывает только первые семь (вместо общих девяти) компонентов, которые объясняют 95% общего отклонения. Единственный свободный пропуск в размере отклонений, учитываемых каждым компонентом, находится между первым и вторым компонентами. Однако первый компонент сам по себе объясняют менее 40% отклонения, поэтому может потребоваться больше компонентов. Можно увидеть, что первые три основных компонента объясняют примерно две трети общей изменчивости в стандартизированных рейтингах, поэтому это может быть разумным способом уменьшить размерности.

Статистика Хотеллинга T-квадрат.

Последний выход из pca является tsquared, который является T от Hotelling², статистическая мера многомерного расстояния каждого наблюдения от центра набора данных. Это аналитический способ найти самые экстремальные точки в данных.

[st2,index] = sort(tsquared,'descend'); % sort in descending order
extreme = index(1);
names(extreme,:)

ans =

New York, NY

Рейтинги для Нью-Йорка самые отдаленные от среднего города США.

Визуализация результатов.

Визуализируйте как ортонормальные коэффициенты основного компонента для каждой переменной, так и счетов основного компонента для каждого наблюдения на одном графике.

biplot(coefforth(:,1:2),'Scores',score(:,1:2),'Varlabels',categories);
axis([-.26 0.6 -.51 .51]);

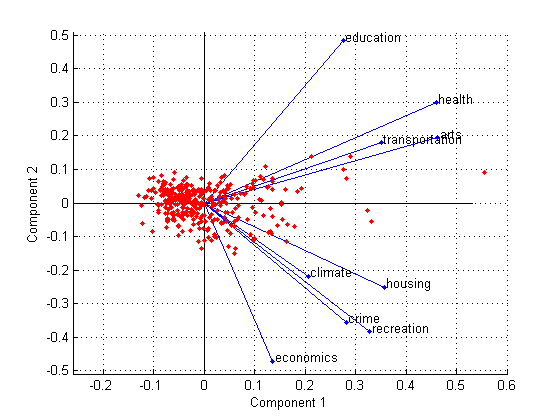
Все девять переменных представлены в этом bi-графике вектором, и направление и длина вектора указывают, как каждая переменная способствует двум основным компонентам на графике. Для примера первый главный компонент на горизонтальной оси имеет положительные коэффициенты для всех девяти переменных. Вот почему девять векторов направлены в правую половину графика. Самые большие коэффициенты в первом главном компоненте являются третьим и седьмым элементами, соответствующими переменным health и arts.

Второй главный компонент на вертикальной оси имеет положительные коэффициенты для переменных education, health, arts, и transportation, и отрицательные коэффициенты для остальных пяти переменных. Это указывает, что второй компонент различает города, которые имеют высокие значения для первого набора переменных и низкие для второго, и города, которые имеют противоположное.

Метки переменных на этом рисунке несколько переполнены. Можно либо исключить VarLabels аргумент пары "имя-значение" при построении графика или выберите и перетащите некоторые метки в лучшие положения с помощью инструмента «Редактировать график» на панели окон рисунка.

Этот 2-D-график также включает точку для каждого из 329 наблюдений с координатами, указывающими счет каждого наблюдения для двух основных компонентов на графике. Для примера точки около левого края этого графика имеют самые низкие счета для первого главного компонента. Точки масштабируются относительно максимального значения баллов и максимальной длины коэффициента, поэтому только их относительные положения могут быть определены из графика.

Можно идентифицировать элементы на графике, выбрав Tools > Data Cursor в окно рисунка. Нажимая переменную (вектор), можно считать метку переменной и коэффициенты для каждого основного компонента. Нажимая на наблюдение (точку), можно считать имя наблюдения и счетов для каждого основного компонента. Можно задать 'Obslabels',names отображение имен наблюдений вместо номеров наблюдений на Data Cursor дисплее.

Создайте трехмерный двоичный график.

Можно также сделать би-график в трёх размерностях.

figure()
biplot(coefforth(:,1:3),'Scores',score(:,1:3),'Obslabels',names);
axis([-.26 0.8 -.51 .51 -.61 .81]);
view([30 40]);

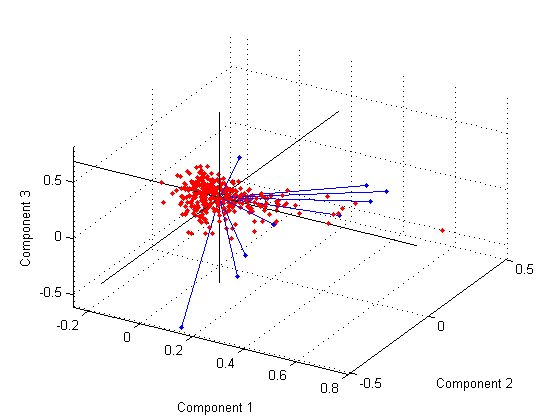
Этот график полезен, если первые две основные координаты недостаточно объясняют отклонение в ваших данных. Можно также повернуть рисунок, чтобы увидеть ее с разных углов, выбрав Tools > Rotate 3D.