В этом разделе описывается, как функционирует Statistics and Machine Learning Toolbox™ quantile и prctile вычисление квантилей и процентилей.
The prctile функция вычисляет процентилы так же, как quantile вычисляет квантования. Следующие шаги вычисления квантилей также верны для процентилей, учитывая тот факт, что для той же выборки данных квантиль при значении Q аналогичен процентилю при значении P = 100 * Q.
quantile первоначально присваивает отсортированные значения в X к (0. 5/ n), (1. 5/ n),..., ([n - 0,5 ]/ n) квантилям. Для примера:
Для вектора данных из шести элементов, таких как {6, 3, 2, 10, 8, 1}, отсортированные элементы {1, 2, 3, 6, 8, 10} соответственно соответствуют (0,5/6), (1,5/6), (2,5/6), (3,5/6), (4,5/6) и (5,5/6) квантилям.
Для вектора данных из пяти элементов, таких как {2, 10, 5, 9, 13}, отсортированные элементы {2, 5, 9, 10, 13} соответственно соответствуют величинам 0,1, 0,3, 0,5, 0,7 и 0,9.
Следующий рисунок иллюстрирует этот подход для вектора данных X = {2, 10, 5, 9, 13}. Первое наблюдение соответствует совокупной вероятности 1/5 = 0,2, второе наблюдение соответствует совокупной вероятности 2/5 = 0,4 и так далее. Функция step на этом рисунке показывает эти совокупные вероятности. quantile вместо этого помещает наблюдения в средние точки, такие что первый соответствует 0,5/5 = 0,1, второй соответствует 1,5/5 = 0,3 и так далее, а затем соединяет эти средние точки. Красные линии на следующем рисунке соединяют средние точки.
Присвоение наблюдений квантилям
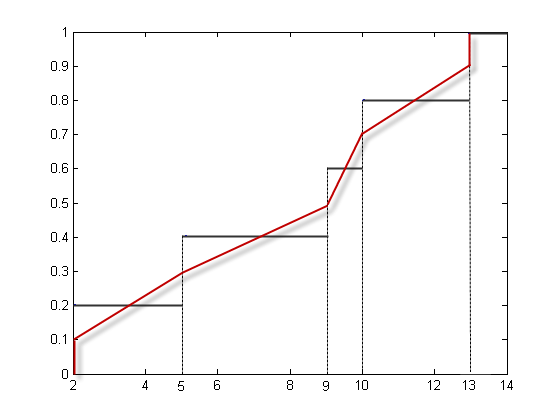
p квантили. Квантования X
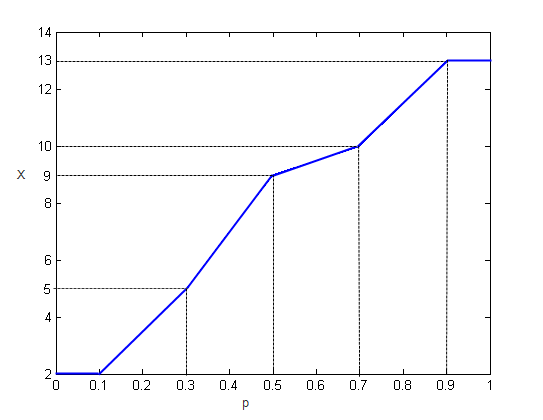
quantile находит любые квантования между значениями данных с помощью линейной интерполяции.
Линейная интерполяция использует линейные полиномы, чтобы аппроксимировать функцию f (x) и создать новые точки данных в области значений известного набора точек данных. Алгебраически, учитывая точки данных (x 1, y 1) и (x 2, y 2), где y 1 = f (x 1) и y 2 = f (x 2), линейная интерполяция находит y = f (x) для заданной x между x 1 и x 2 следующим образом:
Точно так же, если квантиль 1,5/ n находится y 1,5/ n, а квантиль 2,5/ n - y 2,5/ n, то линейная интерполяция находит квантиль 2.3/ n y 2.3/ n как
quantile присваивает квантилям первое и последнее значения X для вероятностей меньше (0 .5/ n) и больше ([n -0.5 ]/ n), соответственно.
[1] Langford, E. «Quartiles in Elementary Statistics», Journal of Statistics Education. Том 14, № 3, 2006.