Линейная регрессия с категориальными ковариатами

В этом примере показано, как выполнить регрессию с категориальными ковариатами, используя категориальные массивы и fitlm.

Загрузите выборочные данные.

load carsmall

Переменная MPG содержит измерения миль на галлон 100 автомобилей-образцов. Модельный год каждого автомобиля находится в переменной Model_Year, и Weight содержит вес каждого автомобиля.

Постройте график сгруппированных данных.

Нарисуйте график поля точек MPG против Weight, сгруппированный по модельным годам.

figure()
gscatter(Weight,MPG,Model_Year,'bgr','x.o')
title('MPG vs. Weight, Grouped by Model Year')

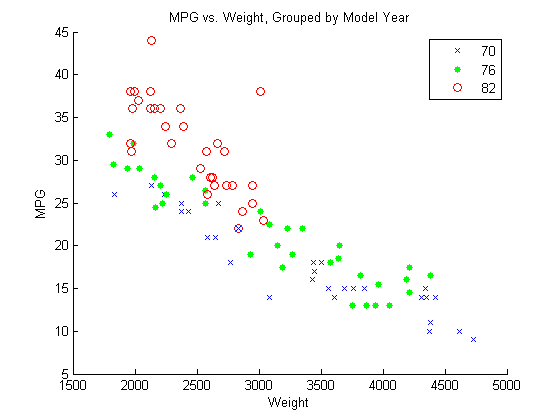
The сгруппированной переменной, Model_Year, имеет три уникальных значения, 70, 76, и 82, соответствующий модельным 1970, 1976 и 1982 годам.

Создайте таблицу и категориальный массив.

Создайте таблицу, которая содержит переменные MPG, Weight, и Model_Year. Преобразуйте переменную Model_Year в категориальный массив.

cars = table(MPG,Weight,Model_Year);
cars.Model_Year = categorical(cars.Model_Year);

Подбор регрессионной модели.

Подбор регрессионной модели с помощью fitlm с MPG как зависимая переменная, и Weight и Model_Year как независимые переменные. Потому что Model_Year является категориальной ковариацией с тремя уровнями, она должна ввести модель как две переменные показателя.

График поля точек предполагает, что наклон MPG против Weight может отличаться для каждого модельного года. Чтобы оценить это, включите условия взаимодействия в весовом году.

Предложенная модель

$E (M P G) = β_{0} + β_{1} W e i g h t + β_{2} I [1976] + β_{3} I [1982] + β_{4} W e i g h t \times I [1976] + β_{5} W e i g h t \times I [1982],$

где I [1976] и I [1982] являются фиктивными переменными, указывающими на 1976 и 1982 лет модели, соответственно. I [1976] принимает значение 1, если модельный год 1976, и принимает значение 0, если нет. I [1982] принимает значение 1, если модельный год 1982, и принимает значение 0, если нет. В этой модели 1970 является базовым годом.

fit = fitlm(cars,'MPG~Weight*Model_Year')

fit = 


Linear regression model:
    MPG ~ 1 + Weight*Model_Year

Estimated Coefficients:
                             Estimate          SE    
                            ___________    __________

    (Intercept)                  37.399        2.1466
    Weight                   -0.0058437    0.00061765
    Model_Year_76                4.6903        2.8538
    Model_Year_82                21.051         4.157
    Weight:Model_Year_76    -0.00082009    0.00085468
    Weight:Model_Year_82     -0.0050551     0.0015636


                             tStat        pValue  
                            ________    __________

    (Intercept)               17.423    2.8607e-30
    Weight                   -9.4612    4.6077e-15
    Model_Year_76             1.6435       0.10384
    Model_Year_82             5.0641    2.2364e-06
    Weight:Model_Year_76    -0.95953       0.33992
    Weight:Model_Year_82     -3.2329     0.0017256


Number of observations: 94, Error degrees of freedom: 88
Root Mean Squared Error: 2.79
R-squared: 0.886,  Adjusted R-Squared: 0.88
F-statistic vs. constant model: 137, p-value = 5.79e-40

Выходные данные регрессии показывают:

fitlm распознает Model_Year как категориальная переменная и создает необходимые переменные индикатора (фиктивные). По умолчанию первый уровень, 70, - это группа ссылки (используйте reordercats для изменения группы ссылки).
Спецификация модели, MPG~Weight*Model_Year, определяет условия первого порядка для Weight и Model_Year, и все взаимодействия.
Модель R² = 0,886, что означает, что изменение миль на галлон уменьшается на 88,6%, когда вы учитываете вес, модельный год и их взаимодействия.

Подобранная модель

$M \hat{P} G = 37.4 - 0.006 W e i g h t + 4.7 I [1976] + 21.1 I [1982] - 0.0008 W e i g h t \times I [1976] - 0.005 W e i g h t \times I [1982] .$

Таким образом, предполагаемые регрессионные уравнения для модельных лет следующие.

Модельный год	Предсказанный MPG против веса
1970	$M \hat{P} G = 37.4 - 0.006 W e i g h t$
1976	$M \hat{P} G = (37.4 + 4.7) - (0.006 + 0.0008) W e i g h t$
1982	$M \hat{P} G = (37.4 + 21.1) - (0.006 + 0.005) W e i g h t$

Модельный год

Предсказанный MPG против веса

1970

$M \hat{P} G = 37.4 - 0.006 W e i g h t$

1976

$M \hat{P} G = (37.4 + 4.7) - (0.006 + 0.0008) W e i g h t$

1982

$M \hat{P} G = (37.4 + 21.1) - (0.006 + 0.005) W e i g h t$

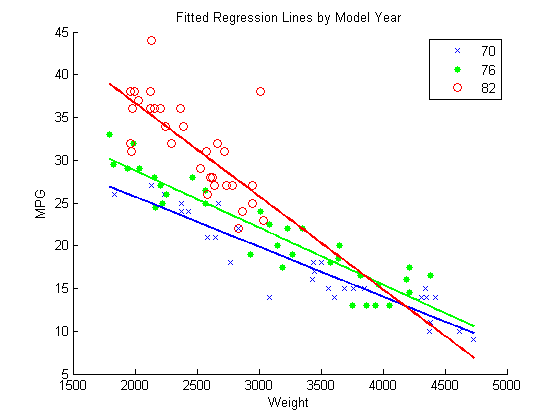
Отношения между MPG и Weight имеет все более отрицательный наклон по мере увеличения модельного года.

Построение графика установленных регрессионных линий.

Постройте график данных и установленных линий регрессии.

w = linspace(min(Weight),max(Weight));

figure()
gscatter(Weight,MPG,Model_Year,'bgr','x.o')
line(w,feval(fit,w,'70'),'Color','b','LineWidth',2)
line(w,feval(fit,w,'76'),'Color','g','LineWidth',2)
line(w,feval(fit,w,'82'),'Color','r','LineWidth',2)
title('Fitted Regression Lines by Model Year')

Тест на различные склоны.

Тест на значительные различия между склонами. Это эквивалентно проверке гипотезы

$\begin{array}{l} H_{0} : β_{4} = β_{5} = 0 \\ H_{A} : β_{i} \neq 0 для в наименьшее один i . \end{array}$

anova(fit)

ans = 

                         SumSq     DF    MeanSq    F         pValue    
    Weight               2050.2     1    2050.2    263.87    3.2055e-28
    Model_Year           807.69     2    403.84    51.976    1.2494e-15
    Weight:Model_Year    81.219     2    40.609    5.2266     0.0071637
    Error                683.74    88    7.7698

Этот выход показывает, что p -value для теста 0.0072 (из строки взаимодействия, Weight:Model_Year), поэтому нулевая гипотеза отклоняется на уровне значимости 0,05. Значение тестовой статистики 5.2266. Степени свободы числителя для теста 2, которое является количеством коэффициентов в нулевой гипотезе.

Существуют достаточные доказательства того, что склоны не равны для всех трех модельных лет.

См. также

anova | categorical | fitlm | reordercats

Документация