Тестовые различия между средними категориями

Этот пример показывает, как проверить на значительные различия между категориями (группами) означает использование t-теста, двухстороннего ANOVA (дисперсионный анализ) и ANOCOVA (ковариационный анализ) анализа .

Цель состоит в том, чтобы определить, зависит ли ожидаемое количество миль на галлон для автомобиля от десятилетия, в котором он был изготовлен, или от места, где он был изготовлен.

Примечание

The nominal и ordinal типы данных массива не рекомендованы. Чтобы представлять упорядоченные и неупорядоченные дискретные нечисловые данные, используйте вместо этого тип данных Категориальные Массивы.

Загрузите выборочные данные.
Создайте фактор для десятилетия производства.
Постройте графики данных, сгруппированных по категориям.
Вычислите сводную статистику.
Проведите t-тест с двумя образцами для средств равной группы.
Создайте коэффициент для места производства.
Объединить категории.
Вычислите сводную статистику.
Проведение двухстороннего Дисперсионный Анализ.
Проведите анализ ANOCOVA.
Используйте интерактивный инструмент.

Загрузите выборочные данные.

load('carsmall')
unique(Model_Year)

Переменная MPG имеет мили на галлон измерения на выборке из 100 автомобилей. Переменные Model_Year и Origin содержать год модели и страну источника для каждого автомобиля.

Первый фактор интереса - десятилетие производства. В данных три года производства.

Создайте фактор для десятилетия производства.

Создайте порядковый массив с именем Decade путем слияния наблюдений с годами 70 и 76 в категорию, помеченную 1970s, и помещая наблюдения из 82 в категорию, помеченную 1980s.

Decade = ordinal(Model_Year,{'1970s','1980s'},[],[70 77 82]);
getlevels(Decade)

ans = 

     1970s      1980s

Постройте графики данных, сгруппированных по категориям.

Рисуйте коробчатый график миль на галлон, сгруппированный по десятилетию производства.

figure()
boxplot(MPG,Decade)
title('Miles per Gallon, Grouped by Decade of Manufacture')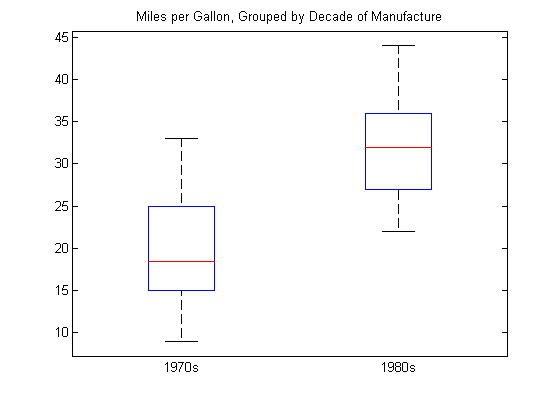

График коробки предполагает, что мили на галлон выше в автомобилях, изготовленных в 1980-х годах по сравнению с 1970-х.

Вычислите сводную статистику.

Вычислите среднее значение и отклонение миль на галлон для каждого десятилетия.

[xbar,s2,grp] = grpstats(MPG,Decade,{'mean','var','gname'})

xbar =

   19.7857
   31.7097


s2 =

   35.1429
   29.0796


grp = 

    '1970s'
    '1980s'

Этот выход показывает, что средние мили на галлон в 1980-х годах были 31.71, по сравнению с 19.79 в 1970-х годах. Отклонения в двух группах одинаковы.

Проведите t-тест с двумя образцами для средств равной группы.

Проведите t-тест с двумя выборками, принимая равные отклонения, чтобы проверить значительное различие между средствами группы. Гипотеза является

$\begin{array}{l} H_{0} : μ_{70} = μ_{80} \\ H_{A} : μ_{70} \neq μ_{80} . \end{array}$

MPG70 = MPG(Decade=='1970s');
MPG80 = MPG(Decade=='1980s');
[h,p] = ttest2(MPG70,MPG80)

h =

     1


p =

   3.4809e-15

Логическое значение 1 указывает, что гипотеза null отклонена на уровне значимости по умолчанию 0,05. Значение p для теста очень маленькое. Существуют достаточные доказательства того, что средние мили на галлон в 1980-х годах отличаются от средних мили на галлон в 1970-х.

Создайте коэффициент для места производства.

Второй фактор интереса - место изготовления. Во-первых, преобразуйте Origin в номинальный массив.

Location = nominal(Origin);
tabulate(Location)

tabulate(Location)
    Value    Count   Percent
   France        4      4.00%
  Germany        9      9.00%
    Italy        1      1.00%
    Japan       15     15.00%
   Sweden        2      2.00%
      USA       69     69.00%

Существует шесть различных стран производства. У европейских стран относительно мало наблюдений.

Объединить категории.

Объедините категории France, Germany, Italy, и Sweden в новую категорию с именем Europe.

Location = mergelevels(Location, ...
    {'France','Germany','Italy','Sweden'},'Europe');
tabulate(Location)

   Value    Count   Percent
   Japan       15     15.00%
     USA       69     69.00%
  Europe       16     16.00%

Вычислите сводную статистику.

Вычислите средние мили на галлон, сгруппированные по месту изготовления.

[xbar,grp] = grpstats(MPG,Location,{'mean','gname'})

xbar =

   31.8000
   21.1328
   26.6667


grp = 

    'Japan'
    'USA'
    'Europe'

Этот результат показывает, что средние мили на галлон являются самыми низкими для выборки автомобилей, произведенных в США

Проведение двухстороннего Дисперсионный Анализ.

Проведите двухсторонний Дисперсионный Анализ, чтобы проверить различия в ожидаемых милях на галлон между уровнями фактора для Decade и Location.

Статистическая модель

$M P G_{i j} = μ + α_{i} + β_{j} + ε_{i j}, i = 1, 2; j = 1, 2, 3,$

где _MPGij - ответ, мили на галлон, для автомобилей, сделанных в десятилетии i на j местоположения. Эффекты лечения для первого фактора, десятилетия производства, являются _αi терминами (ограниченными суммой до нуля). Эффекты обработки для второго фактора, места производства, являются _βj терминами (ограниченными суммой до нуля). Эти _εij являются некоррелированными, обычно распределенными терминами шума.

Гипотезы, которые нужно проверить, являются равными эффектами десятилетия,

$\begin{array}{l} H_{0} : α_{1} = α_{2} = 0 \\ H_{A} : a t l e a s t o n e α_{i} \neq 0, \end{array}$

и равными эффектами для местоположения,

$\begin{array}{l} H_{0} : β_{1} = β_{2} = β_{3} = 0 \\ H_{A} : a t l e a s t o n e β_{j} \neq 0. \end{array}$

Можно провести многофакторный Дисперсионный Анализ с помощью anovan.

anovan(MPG,{Decade,Location},'varnames',{'Decade','Location'});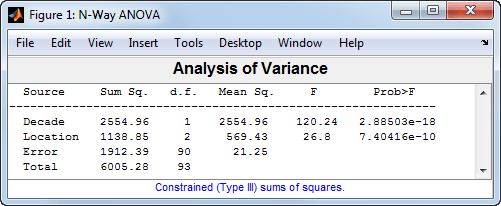

Этот выход показывает результаты двухстороннего Дисперсионный Анализ. p-значение для проверки эффектов равенства десятилетий 2.88503e-18, таким образом, нулевая гипотеза отклоняется на уровне 0,05 значимости. p-значение для проверки эффектов равенства местоположений 7.40416e-10, поэтому эта нулевая гипотеза также отклонена.

Проведите анализ ANOCOVA.

Потенциальным препятствием в этом анализе является вес автомобиля. Ожидается, что автомобили с большим весом будут иметь меньший пробег газа. Включите переменную Weight как непрерывная ковариата в Дисперсионный Анализ; то есть проведите анализ ANOCOVA.

Принимая параллельные линии, статистическая модель является

$M P G_{i j k} = μ + α_{i} + β_{j} + γ W e i g h t_{i j k} + ε_{i j k}, i = 1, 2; j = 1, 2, 3; k = 1, ..., 100.$

Разница между этой моделью и двухсторонней моделью ANOVA заключается в включении непрерывного предиктора, _Weightijk, веса для k-го автомобиля, который был сделан в i-м десятилетии и в j-м месте. Параметр наклона γ.

Добавьте непрерывную ковариату в качестве третьей группы во второй anovan входной параметр. Используйте аргумент пары "имя-значение" Continuous чтобы указать, что Weight (третья группа) непрерывна.

anovan(MPG,{Decade,Location,Weight},'Continuous',3,...
       'varnames',{'Decade','Location','Weight'});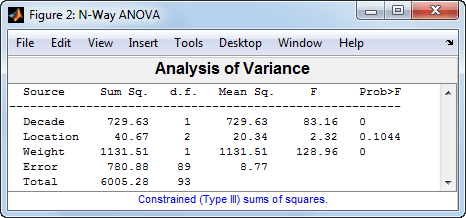

Этот выход показывает, что, когда учитывается вес автомобиля, недостаточно доказательств эффекта производственного местоположения (p-значение = 0.1044).

Используйте интерактивный инструмент.

Можно использовать интерактивную aoctool чтобы исследовать этот результат.

aoctool(Weight,MPG,Location);

Эта команда открывает три диалоговых окна. В диалоговом окне ANOCOVA Prediction Plot выберите Separate Means модель.

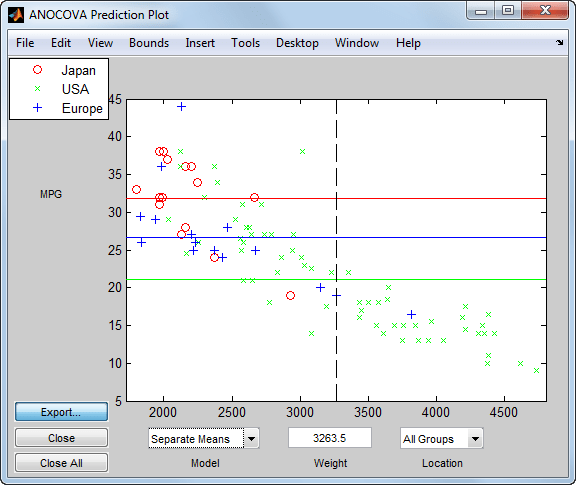
Этот выход показывает, что, когда вы не включаете Weight в модели существуют довольно большие различия в ожидаемых милях на галлон среди трех производственных мест. Обратите внимание, что здесь модель не настраивается на десятилетие производства.

Теперь выберите модель Parallel Lines.

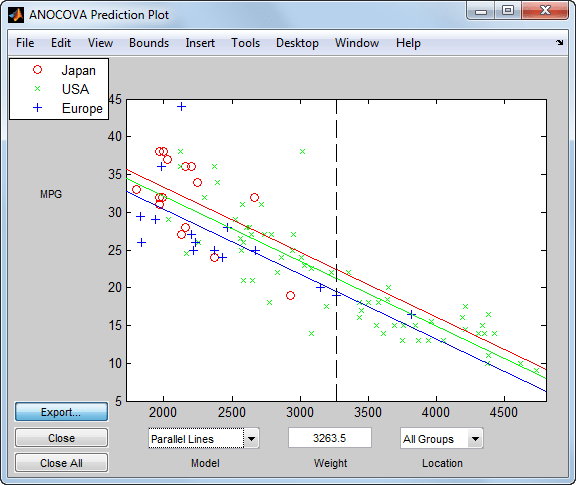
Когда вы включаете Weight в модели различие в ожидаемых милях на галлон среди трех производственных мест намного меньше.

См. также

Документация