Можно использовать машину опорных векторов (SVM), когда ваши данные имеют ровно два класса. SVM классифицирует данные, находя лучшую гиперплоскость, которая отделяет все точки данных одного класса от точек другого класса. Гиперплоскость best для SVM означает плату с самым большим margin между этими двумя классами. Поле означает максимальную ширину перекрытия, параллельную гиперплоскости, которая не имеет внутренних точек данных.
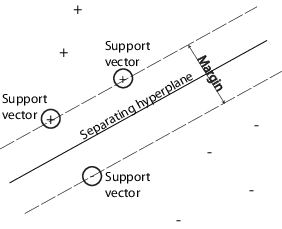
support vectors являются точками данных, которые ближе всего к разделяющей гиперплоскости; эти точки находятся на контуре перекрытия. Следующий рисунок иллюстрирует эти определения с + указанием точек данных типа 1 и - указанием точек данных типа -1.
Математическая формулировка: Primal. Эта дискуссия следует за Хасти, Тибширани и Фридманом [1] и Кристианини и Шо-Тейлором [2].
Данные для обучения являются набором точек (векторов) xj наряду с yj их категорий. Для некоторых d размерности xj ∊ Rd, и yj = ± 1. Уравнение гиперплоскости
где β ∊ Rd а b - действительное число.
Следующая задача определяет best, разделяющую гиперплоскость (то есть контур принятия решения). Найдите β и b, которые минимизируют ||<reservedrangesplaceholder2>|| так, что для всех точек данных (xj, yj),
Поддерживающие векторы являются xj на контуре, те для которых
Для математического удобства задача обычно задается как эквивалентная задача минимизации . Это квадратичная задача программирования. Оптимальное решение позволяет классифицировать вектор z следующим образом:
является classification score и представляет расстояние, z находится от контура принятия решения.
Математическая формулировка: Dual. Вычислительно проще решить задачу двойного квадратичного программирования. Чтобы получить двойственное, примите положительные множители Лагранжа αj умноженные на каждое ограничение, и вычитайте из целевой функции:
где вы ищете стационарную точку LP над β и b. Устанавливая градиент LP равным 0, вы получаете
| (1) |
Подстановка в LP, вы получаете двойственную LD:
который вы максимизируете над αj ≥ 0. В целом многие αj на максимуме 0. Ненулевые αj в решении двойственной задачи определяют гиперплоскость, как видно из Уравнения 1, которое дает β как сумму αjyjxj. Точки данных xj соответствующие ненулевым αj, являются support vectors.
Производная LD относительно ненулевого αj равна 0 при оптимуме. Это дает
В частности, это дает значение b в решении, принимая любое j с ненулевым αj.
Двойственное - стандартная квадратичная задача программирования. Для примера, Optimization Toolbox™ quadprog Решатель (Optimization Toolbox) решает этот тип задачи.
Данные могут не разрешать разделение гиперплоскости. В этом случае SVM может использовать soft margin, означающую гиперплоскость, которая разделяет многие, но не все точки данных.
Существует две стандартные формулировки мягких полей. Оба включают добавление переменных slack ξj и C параметра штрафа.
The L1-norm задача:
таким, что
The L1-norm относится к использованию ξj в качестве переменных slack вместо их квадратов. Три опции решателя SMO, ISDA, и L1QP из fitcsvm минимизировать L1-norm задача.
The L2-norm задача:
с учетом тех же ограничений.
В этих формулировках можно увидеть, что увеличение C придает больше веса переменным slack ξj, что означает, что оптимизация пытается сделать более строгое разделение между классами. Эквивалентно, уменьшение C к 0 делает неправильную классификацию менее важной.
Математическая формулировка: Dual. Для более простых вычислений рассмотрим L1 двойственная проблема этой мягкой формулировки. Используя множители Лагранжа μj, функцию минимизации для L1-norm задача:
где вы ищете стационарную точку LP по β, b и положительным ξj. Устанавливая градиент LP равным 0, вы получаете
Эти уравнения приводят непосредственно к двойственной формулировке:
удовлетворяющее ограничениям
Конечный набор неравенств, 0 ≤ αj ≤ C, показывает, почему C иногда называют box constraint. C сохраняет допустимые значения множителей Лагранжа αj в «кубе», ограниченной области.
Градиентное уравнение для b дает решение, b в терминах множества ненулевых αj, которые соответствуют поддерживающим векторам.
Вы можете написать и решить двойственный из L2-norm задача аналогично. Для получения дополнительной информации см. Christianini и Shawe-Taylor [2], глава 6.
fitcsvm Реализация. Обе задачи с двойным мягким запасом являются квадратичными задачами программирования. Внутренне, fitcsvm имеет несколько различных алгоритмов для решения задач.
Для классовой или двоичной классификации, если вы не задаете долю ожидаемых выбросов в данных (см OutlierFraction), тогда решателем по умолчанию является Sequential Minimal Optimization (SMO). SMO минимизирует задачу с одной нормой серией двухточечных минимизаций. Во время оптимизации SMO уважает линейное ограничение и явно включает в себя члена в модели смещения. SMO относительно быстро. Для получения дополнительной информации о SMO см. раздел [3].
Для двоичной классификации, если вы задаете часть ожидаемых выбросов в данных, то решателем по умолчанию является итерационный алгоритм единичных данных. Как и SMO, ISDA решает задачу с одной нормой. В отличие от SMO, ISDA минимизирует последовательностью на одноточечных минимизациях, не уважает линейное ограничение и явно не включает члена в модели смещения. Для получения дополнительной информации об ISDA см. [4].
Для одноклассовой или двоичной классификации, и если у вас есть лицензия Optimization Toolbox, можно выбрать использование quadprog (Optimization Toolbox), чтобы решить задачу с одной нормой. quadprog использует большую часть памяти, но решает квадратичные программы с высокой степенью точности. Для получения дополнительной информации смотрите Определение квадратичного программирования (Optimization Toolbox).
Некоторые задачи двоичной классификации не имеют простой гиперплоскости в качестве полезного критерия разделения. Для этих задач существует вариант математического подхода, который сохраняет почти всю простоту SVM-разделительной гиперплоскости.
Этот подход использует следующие результаты теории воспроизведения ядер:
Существует класс функций G (x 1, x 2) со следующим свойством. Существует линейное пространство S и функция φ отображения x чтобы S таким, что
G (x 1, <reservedrangesplaceholder4> 2) = <φ (x 1), φ (x 2)>.
Точечный продукт происходит в пространственном S.
Этот класс функций включает:
Полиномы: Для некоторых положительных целочисленных p,
G (x 1, <reservedrangesplaceholder2> 2) = (1 + <reservedrangesplaceholder1> 1 <reservedrangesplaceholder0> 2)p.
Функция радиального базиса (Гауссов):
G (x 1, x 2) = exp (- ∥ x 1- x 2) ∥2).
Многослойный перцептрон или сигмоид (нейронная сеть): Для положительного числа p 1 и отрицательного числа p 2,
G (x 1, x 2) = tanh (p 1 x 1 − x 2 + p 2).
Примечание
Не каждый набор p 1 и p 2 дает допустимое повторяющееся ядро.
fitcsvm не поддерживает сигмоидное ядро. Вместо этого можно задать сигмоидное ядро и задать его при помощи 'KernelFunction' аргумент пары "имя-значение". Для получения дополнительной информации см. Train классификатора SVM с использованием пользовательского ядра».
Математический подход с использованием ядер опирается на вычислительный метод гиперплоскостей. Все расчеты для классификации гиперплоскостей используют не что иное, как точечные продукты. Поэтому нелинейные ядра могут использовать идентичные вычисления и алгоритмы решения и получить нелинейные классификаторы. Получившиеся классификаторы являются гиперсерфалями в некоторых пространствах S, но пространство S не нужно идентифицировать или исследовать.
Как и в любой модели контролируемого обучения, вы сначала обучаете машину опорных векторов, а затем пересекаете валидацию классификатора. Используйте обученную машину, чтобы классифицировать (предсказать) новые данные. В сложение, чтобы получить удовлетворительную прогнозирующую точность, можно использовать различные функции ядра SVM, и необходимо настроить параметры функций ядра.
Обучите и опционально перекрестно проверьте классификатор SVM с помощью fitcsvm. Наиболее распространенным синтаксисом является:
SVMModel = fitcsvm(X,Y,'KernelFunction','rbf',...
'Standardize',true,'ClassNames',{'negClass','posClass'});Входные входы:
X - Матрица данных предиктора, где каждая строка является одним наблюдением, и каждый столбец является одним предиктором.
Y - Массив меток классов с каждой строкой, соответствующей значению соответствующей строки в X. Y может быть категориальными символьными или строковыми массивами, логическим или числовым вектором или массивом ячеек из векторов символов.
KernelFunction - Значение по умолчанию 'linear' для двухклассного обучения, которое разделяет данные гиперплоской. Значение 'gaussian' (или 'rbf') является по умолчанию для одноклассного обучения и задает использование ядра Гауссова (или функции радиального базиса). Важным шагом для успешного обучения классификатора SVM является выбор соответствующей функции ядра.
Standardize - Флаг, указывающий, должно ли программное обеспечение стандартизировать предикторы перед обучением классификатора.
ClassNames - Различает отрицательный и положительный классы или определяет, какие классы включать в данные. Отрицательный класс является первым элементом (или строкой символьного массива), например 'negClass', и положительный класс является вторым элементом (или строкой символьного массива), например 'posClass'. ClassNames должен быть совпадающего типа данных, что и Y. Рекомендуется задавать имена классов, особенно если вы сравниваете эффективность различных классификаторов.
Получившаяся, обученная модель (SVMModel) содержит оптимизированные параметры из алгоритма SVM, позволяющие классифицировать новые данные.
Для получения дополнительных пар "имя-значение", которые можно использовать для управления обучением, см. fitcsvm страница с описанием.
Классификация новых данных с помощью predict. Синтаксис для классификации новых данных с помощью обученного классификатора SVM (SVMModelявляется:
[label,score] = predict(SVMModel,newX);
Получившийся вектор, label, представляет классификацию каждой строки в X. score является n -by-2 матрицей мягких счетов. Каждая строка соответствует строке в X, что является новым наблюдением. Первый столбец содержит счета для наблюдений, классифицируемых в отрицательном классе, а второй столбец содержит наблюдения счетов, классифицируемые в положительном классе.
Чтобы оценить апостериорные вероятности, а не счета, сначала передайте обученный классификатор SVM (SVMModel) к fitPosterior, которая подходит к функции счета-к-апостериорной-вероятностному преобразованию в счета. Синтаксис:
ScoreSVMModel = fitPosterior(SVMModel,X,Y);
Свойство ScoreTransform классификатора ScoreSVMModel содержит оптимальную функцию преобразования. Передайте ScoreSVMModel на predict. Вместо того, чтобы возвращать счета, выходной аргумент score содержит апостериорные вероятности наблюдения, классифицируемого в отрицательном значении (столбец 1 score) или положительный (столбец 2 score) класс.
Используйте 'OptimizeHyperparameters' Аргумент пары "имя-значение" из fitcsvm чтобы найти значения параметров, которые минимизируют потери при перекрестной проверке. Подходящие параметры 'BoxConstraint', 'KernelFunction', 'KernelScale', 'PolynomialOrder', и 'Standardize'. Для получения примера смотрите Оптимизацию классификатора SVM Подгонки Используя Байесовскую оптимизацию. Кроме того, можно использовать bayesopt функция, как показано на Оптимизации классификатора SVM с перекрестной проверкой с использованием bayesopt. bayesopt функция позволяет более гибко настраивать оптимизацию. Вы можете использовать bayesopt функция для оптимизации любых параметров, включая параметры, которые не имеют права оптимизировать, когда вы используете fitcsvm функция.
Можно также попробовать настроить параметры классификатора вручную согласно этой схеме:
Передайте данные в fitcsvm, и установите аргумент пары "имя-значение" 'KernelScale','auto'. Предположим, что обученная модель SVM называется SVMModel. Программа использует эвристическую процедуру, чтобы выбрать шкалу ядра. Эвристическая процедура использует субдискретизацию. Поэтому, чтобы воспроизвести результаты, установите начальное число случайных чисел, используя rng перед обучением классификатора.
Перекрестная проверка классификатора путем передачи его в crossval. По умолчанию программное обеспечение проводит 10-кратную перекрестную валидацию.
Передайте перекрестно проверенную модель SVM, чтобы kfoldLoss для оценки и сохранения ошибки классификации.
Переобучите классификатор SVM, но измените 'KernelScale' и 'BoxConstraint' Аргументы пары "имя-значение".
BoxConstraint - Одна из стратегий состоит в том, чтобы попробовать геометрическую последовательность прямоугольного параметра ограничения. Например, примите 11 значений, из 1e-5 на 1e5 в 10 раз. Увеличение BoxConstraint может уменьшить количество векторов поддержки, но также может увеличить время обучения.
KernelScale - Одна из стратегий состоит в том, чтобы попробовать геометрическую последовательность параметра sigma RBF, масштабируемого в исходной шкале ядра. Сделайте это путем:
Получение исходной шкалы ядра, например ks, использование записи через точку: ks = SVMModel.KernelParameters.Scale.
Используйте как новые коэффициенты шкалы ядра оригинала. Для примера умножьте ks по 11 значениям 1e-5 на 1e5, увеличение в 10 раз.
Выберите модель, которая приводит к самой низкой ошибке классификации. Вы, возможно, захотите дополнительно уточнить свои параметры, чтобы получить лучшую точность. Начните с начальных параметров и выполните другой шаг перекрестной валидации, на этот раз используя коэффициент 1.2.
Этот пример показывает, как сгенерировать нелинейный классификатор с функцией Гауссова ядра. Сначала сгенерируйте один класс точек внутри единичного диска в двух измерениях и другой класс точек в кольцевом пространстве от радиуса 1 до радиуса 2. Затем генерирует классификатор, основанный на данных с ядром функции Гауссова радиального базиса. Линейный классификатор по умолчанию, очевидно, непригоден для этой задачи, поскольку модель имеет круговую симметрию. Установите прямоугольный параметр ограничения равным Inf сделать строгую классификацию, означающую отсутствие неправильной классификации обучающих точек. Другие функции ядра могут не работать с этим строгим прямоугольным ограничением, поскольку они могут оказаться неспособными предоставить строгую классификацию. Даже при том, что классификатор rbf может разделять классы, результат может быть переобучен.
Сгенерируйте 100 точек, равномерно распределенных в единичном диске. Для этого сгенерируйте радиус r как квадратный корень равномерной случайной переменной, сгенерируйте угол t равномерно в (0, ) и поставить точку (r cos (t), r sin (t)).
rng(1); % For reproducibility r = sqrt(rand(100,1)); % Radius t = 2*pi*rand(100,1); % Angle data1 = [r.*cos(t), r.*sin(t)]; % Points
Сгенерируйте 100 точек равномерно распределенных в кольцевом пространстве. Радиус снова пропорционален квадратному корню, на этот раз квадратному корню равномерного распределения от 1 до 4.
r2 = sqrt(3*rand(100,1)+1); % Radius t2 = 2*pi*rand(100,1); % Angle data2 = [r2.*cos(t2), r2.*sin(t2)]; % points
Постройте график точек и постройте графики радиусов 1 и 2 для сравнения.
figure; plot(data1(:,1),data1(:,2),'r.','MarkerSize',15) hold on plot(data2(:,1),data2(:,2),'b.','MarkerSize',15) ezpolar(@(x)1);ezpolar(@(x)2); axis equal hold off

Поместите данные в одну матрицу и сделайте вектор классификаций.
data3 = [data1;data2]; theclass = ones(200,1); theclass(1:100) = -1;
Обучите классификатор SVM с KernelFunction установлено на 'rbf' и BoxConstraint установлено на Inf. Постройте график контура принятия решений и отметьте векторы поддержки.
%Train the SVM Classifier cl = fitcsvm(data3,theclass,'KernelFunction','rbf',... 'BoxConstraint',Inf,'ClassNames',[-1,1]); % Predict scores over the grid d = 0.02; [x1Grid,x2Grid] = meshgrid(min(data3(:,1)):d:max(data3(:,1)),... min(data3(:,2)):d:max(data3(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; [~,scores] = predict(cl,xGrid); % Plot the data and the decision boundary figure; h(1:2) = gscatter(data3(:,1),data3(:,2),theclass,'rb','.'); hold on ezpolar(@(x)1); h(3) = plot(data3(cl.IsSupportVector,1),data3(cl.IsSupportVector,2),'ko'); contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],'k'); legend(h,{'-1','+1','Support Vectors'}); axis equal hold off

fitcsvm генерирует классификатор, который близок к кругу радиуса 1. Различие обусловлено случайными обучающими данными.
Обучение с параметрами по умолчанию делает более близкий круговой контур классификации, но такую, которая ошибочно классифицирует некоторые обучающие данные. Кроме того, значение по умолчанию BoxConstraint является 1и, следовательно, существует больше поддержка векторов.
cl2 = fitcsvm(data3,theclass,'KernelFunction','rbf'); [~,scores2] = predict(cl2,xGrid); figure; h(1:2) = gscatter(data3(:,1),data3(:,2),theclass,'rb','.'); hold on ezpolar(@(x)1); h(3) = plot(data3(cl2.IsSupportVector,1),data3(cl2.IsSupportVector,2),'ko'); contour(x1Grid,x2Grid,reshape(scores2(:,2),size(x1Grid)),[0 0],'k'); legend(h,{'-1','+1','Support Vectors'}); axis equal hold off

В этом примере показано, как использовать пользовательскую функцию ядра, такую как сигмоидное ядро, для обучения классификаторов SVM и настройки параметров пользовательской функции ядра.
Сгенерируйте случайный набор точек в модуль круге. Маркируйте точки в первом и третьем квадрантах как принадлежащие положительному классу, и точки во втором и четвертом квадрантах в отрицательном классе.
rng(1); % For reproducibility n = 100; % Number of points per quadrant r1 = sqrt(rand(2*n,1)); % Random radii t1 = [pi/2*rand(n,1); (pi/2*rand(n,1)+pi)]; % Random angles for Q1 and Q3 X1 = [r1.*cos(t1) r1.*sin(t1)]; % Polar-to-Cartesian conversion r2 = sqrt(rand(2*n,1)); t2 = [pi/2*rand(n,1)+pi/2; (pi/2*rand(n,1)-pi/2)]; % Random angles for Q2 and Q4 X2 = [r2.*cos(t2) r2.*sin(t2)]; X = [X1; X2]; % Predictors Y = ones(4*n,1); Y(2*n + 1:end) = -1; % Labels
Постройте график данных.
figure;
gscatter(X(:,1),X(:,2),Y);
title('Scatter Diagram of Simulated Data')

Написание функции, которая принимает две матрицы в пространстве признаков как входы и преобразует их в матрицу Грамма, используя сигмоидное ядро.
function G = mysigmoid(U,V) % Sigmoid kernel function with slope gamma and intercept c gamma = 1; c = -1; G = tanh(gamma*U*V' + c); end
Сохраните этот код как файл с именем mysigmoid на пути MATLAB ®.
Обучите классификатор SVM с помощью функции сигмоидного ядра. Рекомендуется стандартизировать данные.
Mdl1 = fitcsvm(X,Y,'KernelFunction','mysigmoid','Standardize',true);
Mdl1 является ClassificationSVM классификатор, содержащий предполагаемые параметры.
Постройте график данных и идентифицируйте векторы поддержки и контур принятия решения.
% Compute the scores over a grid d = 0.02; % Step size of the grid [x1Grid,x2Grid] = meshgrid(min(X(:,1)):d:max(X(:,1)),... min(X(:,2)):d:max(X(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; % The grid [~,scores1] = predict(Mdl1,xGrid); % The scores figure; h(1:2) = gscatter(X(:,1),X(:,2),Y); hold on h(3) = plot(X(Mdl1.IsSupportVector,1),... X(Mdl1.IsSupportVector,2),'ko','MarkerSize',10); % Support vectors contour(x1Grid,x2Grid,reshape(scores1(:,2),size(x1Grid)),[0 0],'k'); % Decision boundary title('Scatter Diagram with the Decision Boundary') legend({'-1','1','Support Vectors'},'Location','Best'); hold off

Можно настроить параметры ядра в попытке улучшить форму контура принятия решения. Это также может снизить коэффициент неправильной классификации внутри выборки, но сначала необходимо определить показатель неправильной классификации вне выборки.
Определите частоту неправильной классификации вне выборки с помощью 10-кратной перекрестной валидации.
CVMdl1 = crossval(Mdl1); misclass1 = kfoldLoss(CVMdl1); misclass1
misclass1 =
0.1350
Показатель неправильной классификации вне выборки составляет 13,5%.
Напишите другую сигмоидную функцию, но Установите gamma = 0.5;.
function G = mysigmoid2(U,V) % Sigmoid kernel function with slope gamma and intercept c gamma = 0.5; c = -1; G = tanh(gamma*U*V' + c); end
Сохраните этот код как файл с именем mysigmoid2 на пути MATLAB ®.
Обучите другой классификатор SVM с помощью скорректированного сигмоидного ядра. Постройте график данных и области принятия решений и определите частоту неправильной классификации вне выборки.
Mdl2 = fitcsvm(X,Y,'KernelFunction','mysigmoid2','Standardize',true); [~,scores2] = predict(Mdl2,xGrid); figure; h(1:2) = gscatter(X(:,1),X(:,2),Y); hold on h(3) = plot(X(Mdl2.IsSupportVector,1),... X(Mdl2.IsSupportVector,2),'ko','MarkerSize',10); title('Scatter Diagram with the Decision Boundary') contour(x1Grid,x2Grid,reshape(scores2(:,2),size(x1Grid)),[0 0],'k'); legend({'-1','1','Support Vectors'},'Location','Best'); hold off CVMdl2 = crossval(Mdl2); misclass2 = kfoldLoss(CVMdl2); misclass2
misclass2 =
0.0450

После корректировки сигмоидного склона новый контур принятия решений, по-видимому, обеспечивает лучшую подгонку внутри выборки, а коэффициент перекрестной валидации сокращается более чем на 66%.
В этом примере показано, как оптимизировать классификацию SVM с помощью fitcsvm функции и OptimizeHyperparameters Пара "имя-значение". Классификация работает с местоположениями точек из смешанной гауссовской модели. В The Elements of Statistical Learning, Hastie, Tibshirani, and Friedman (2009), страница 17 описывает модель. Модель начинается с генерации 10 базовых точек для «зеленого» класса, распределенных как 2-D независимых нормалей со средним значением (1,0) и единичным отклонением. Это также генерирует 10 базовых точек для «красного» класса, распределенных как 2-D независимых нормалей со средней (0,1) и единичным отклонением. Для каждого класса (зеленого и красного) сгенерируйте 100 случайных точек следующим образом:
Выберите базовую точку m соответствующего цвета случайным образом.
Сгенерируйте независимую случайную точку с 2-D нормальным распределением со средним m и I/5 отклонения, где I является единичной матрицей 2 на 2. В этом примере используйте I/50 отклонений, чтобы более четко показать преимущество оптимизации.
Сгенерируйте точки и классификатор
Сгенерируйте 10 базовых точек для каждого класса.
rng default % For reproducibility grnpop = mvnrnd([1,0],eye(2),10); redpop = mvnrnd([0,1],eye(2),10);
Просмотрите базовые точки.
plot(grnpop(:,1),grnpop(:,2),'go') hold on plot(redpop(:,1),redpop(:,2),'ro') hold off

Поскольку некоторые красные базовые точки близки к зеленым базовым точкам, может быть трудно классифицировать точки данных на основе одного местоположения.
Сгенерируйте 100 точек данных каждого класса.
redpts = zeros(100,2);grnpts = redpts; for i = 1:100 grnpts(i,:) = mvnrnd(grnpop(randi(10),:),eye(2)*0.02); redpts(i,:) = mvnrnd(redpop(randi(10),:),eye(2)*0.02); end
Просмотрите точки данных.
figure plot(grnpts(:,1),grnpts(:,2),'go') hold on plot(redpts(:,1),redpts(:,2),'ro') hold off

Подготовка данных к классификации
Поместите данные в одну матрицу и сделайте вектор grp который помечает класс каждой точки.
cdata = [grnpts;redpts];
grp = ones(200,1);
% Green label 1, red label -1
grp(101:200) = -1;Подготовка перекрестной проверки
Настройте раздел для перекрестной проверки. Этот шаг исправляет train и тестовые наборы, которые оптимизация использует на каждом шаге.
c = cvpartition(200,'KFold',10);Оптимизация подгонки
Чтобы найти хорошую подгонку, то есть с низкой потерей перекрестной валидации, установите опции, чтобы использовать байесовскую оптимизацию. Используйте тот же раздел перекрестной проверки c во всех оптимизациях.
Для воспроизводимости используйте 'expected-improvement-plus' функция сбора.
opts = struct('Optimizer','bayesopt','ShowPlots',true,'CVPartition',c,... 'AcquisitionFunctionName','expected-improvement-plus'); svmmod = fitcsvm(cdata,grp,'KernelFunction','rbf',... 'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions',opts)
|=====================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | | | result | | runtime | (observed) | (estim.) | | | |=====================================================================================================| | 1 | Best | 0.345 | 0.20756 | 0.345 | 0.345 | 0.00474 | 306.44 | | 2 | Best | 0.115 | 0.14872 | 0.115 | 0.12678 | 430.31 | 1.4864 | | 3 | Accept | 0.52 | 0.12556 | 0.115 | 0.1152 | 0.028415 | 0.014369 | | 4 | Accept | 0.61 | 0.16264 | 0.115 | 0.11504 | 133.94 | 0.0031427 | | 5 | Accept | 0.34 | 0.14384 | 0.115 | 0.11504 | 0.010993 | 5.7742 | | 6 | Best | 0.085 | 0.15049 | 0.085 | 0.085039 | 885.63 | 0.68403 | | 7 | Accept | 0.105 | 0.12919 | 0.085 | 0.085428 | 0.3057 | 0.58118 | | 8 | Accept | 0.21 | 0.15841 | 0.085 | 0.09566 | 0.16044 | 0.91824 | | 9 | Accept | 0.085 | 0.18577 | 0.085 | 0.08725 | 972.19 | 0.46259 | | 10 | Accept | 0.1 | 0.1428 | 0.085 | 0.090952 | 990.29 | 0.491 | | 11 | Best | 0.08 | 0.14182 | 0.08 | 0.079362 | 2.5195 | 0.291 | | 12 | Accept | 0.09 | 0.12232 | 0.08 | 0.08402 | 14.338 | 0.44386 | | 13 | Accept | 0.1 | 0.13074 | 0.08 | 0.08508 | 0.0022577 | 0.23803 | | 14 | Accept | 0.11 | 0.15858 | 0.08 | 0.087378 | 0.2115 | 0.32109 | | 15 | Best | 0.07 | 0.15241 | 0.07 | 0.081507 | 910.2 | 0.25218 | | 16 | Best | 0.065 | 0.15047 | 0.065 | 0.072457 | 953.22 | 0.26253 | | 17 | Accept | 0.075 | 0.15512 | 0.065 | 0.072554 | 998.74 | 0.23087 | | 18 | Accept | 0.295 | 0.14554 | 0.065 | 0.072647 | 996.18 | 44.626 | | 19 | Accept | 0.07 | 0.22102 | 0.065 | 0.06946 | 985.37 | 0.27389 | | 20 | Accept | 0.165 | 0.14178 | 0.065 | 0.071622 | 0.065103 | 0.13679 | |=====================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | | | result | | runtime | (observed) | (estim.) | | | |=====================================================================================================| | 21 | Accept | 0.345 | 0.12463 | 0.065 | 0.071764 | 971.7 | 999.01 | | 22 | Accept | 0.61 | 0.17579 | 0.065 | 0.071967 | 0.0010168 | 0.0010005 | | 23 | Accept | 0.345 | 0.1675 | 0.065 | 0.071959 | 0.0010674 | 999.18 | | 24 | Accept | 0.35 | 0.13478 | 0.065 | 0.071863 | 0.0010003 | 40.628 | | 25 | Accept | 0.24 | 0.23822 | 0.065 | 0.072124 | 996.55 | 10.423 | | 26 | Accept | 0.61 | 0.14478 | 0.065 | 0.072068 | 958.64 | 0.0010026 | | 27 | Accept | 0.47 | 0.13262 | 0.065 | 0.07218 | 993.69 | 0.029723 | | 28 | Accept | 0.3 | 0.15652 | 0.065 | 0.072291 | 993.15 | 170.01 | | 29 | Accept | 0.16 | 0.31079 | 0.065 | 0.072104 | 992.81 | 3.8594 | | 30 | Accept | 0.365 | 0.1375 | 0.065 | 0.072112 | 0.0010017 | 0.044287 |


__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 48.9578 seconds
Total objective function evaluation time: 4.7979
Best observed feasible point:
BoxConstraint KernelScale
_____________ ___________
953.22 0.26253
Observed objective function value = 0.065
Estimated objective function value = 0.073726
Function evaluation time = 0.15047
Best estimated feasible point (according to models):
BoxConstraint KernelScale
_____________ ___________
985.37 0.27389
Estimated objective function value = 0.072112
Estimated function evaluation time = 0.16248
svmmod =
ClassificationSVM
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [-1 1]
ScoreTransform: 'none'
NumObservations: 200
HyperparameterOptimizationResults: [1x1 BayesianOptimization]
Alpha: [77x1 double]
Bias: -0.2352
KernelParameters: [1x1 struct]
BoxConstraints: [200x1 double]
ConvergenceInfo: [1x1 struct]
IsSupportVector: [200x1 logical]
Solver: 'SMO'
Properties, Methods
Найдите потерю оптимизированной модели.
lossnew = kfoldLoss(fitcsvm(cdata,grp,'CVPartition',c,'KernelFunction','rbf',... 'BoxConstraint',svmmod.HyperparameterOptimizationResults.XAtMinObjective.BoxConstraint,... 'KernelScale',svmmod.HyperparameterOptimizationResults.XAtMinObjective.KernelScale))
lossnew = 0.0650
Эта потеря аналогична потере, сообщенной в выходе оптимизации под «Наблюдаемое значение целевой функции».
Визуализируйте оптимизированный классификатор.
d = 0.02; [x1Grid,x2Grid] = meshgrid(min(cdata(:,1)):d:max(cdata(:,1)),... min(cdata(:,2)):d:max(cdata(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; [~,scores] = predict(svmmod,xGrid); figure; h = nan(3,1); % Preallocation h(1:2) = gscatter(cdata(:,1),cdata(:,2),grp,'rg','+*'); hold on h(3) = plot(cdata(svmmod.IsSupportVector,1),... cdata(svmmod.IsSupportVector,2),'ko'); contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],'k'); legend(h,{'-1','+1','Support Vectors'},'Location','Southeast'); axis equal hold off

В этом примере показано, как предсказать апостериорные вероятности моделей SVM по сетке наблюдений, а затем построить график апостериорных вероятностей по сетке. Графическое изображение апостериорных вероятностей открывает контуры принятия решений.
Загрузите набор данных радужки Фишера. Обучите классификатор, используя длины и ширины лепестков, и удалите виды virginica из данных.
load fisheriris classKeep = ~strcmp(species,'virginica'); X = meas(classKeep,3:4); y = species(classKeep);
Обучите классификатор SVM с помощью данных. Рекомендуется определить порядок классов.
SVMModel = fitcsvm(X,y,'ClassNames',{'setosa','versicolor'});
Оцените оптимальную функцию преобразования счета.
rng(1); % For reproducibility
[SVMModel,ScoreParameters] = fitPosterior(SVMModel); Warning: Classes are perfectly separated. The optimal score-to-posterior transformation is a step function.
ScoreParameters
ScoreParameters = struct with fields:
Type: 'step'
LowerBound: -0.8431
UpperBound: 0.6897
PositiveClassProbability: 0.5000
Оптимальная функция преобразования счета является шаговой функцией, потому что классы разделимы. Поля LowerBound и UpperBound от ScoreParameters указать нижнюю и верхнюю конечные точки интервала счетов, соответствующего наблюдениям в разделяющих класс гиперплоскостях (поле). Никакое наблюдение за обучением не подпадает под поле. Если новый счет находится в интервале, то программное обеспечение присваивает соответствующему наблюдению апостериорную вероятность положительного класса, то есть значение в PositiveClassProbability область ScoreParameters.
Задайте сетку значений в наблюдаемом пространстве предикторов. Спрогнозируйте апостериорные вероятности для каждого образца в сетке.
xMax = max(X); xMin = min(X); d = 0.01; [x1Grid,x2Grid] = meshgrid(xMin(1):d:xMax(1),xMin(2):d:xMax(2)); [~,PosteriorRegion] = predict(SVMModel,[x1Grid(:),x2Grid(:)]);
Постройте график апостериорной области вероятностей положительного класса и обучающих данных.
figure; contourf(x1Grid,x2Grid,... reshape(PosteriorRegion(:,2),size(x1Grid,1),size(x1Grid,2))); h = colorbar; h.Label.String = 'P({\it{versicolor}})'; h.YLabel.FontSize = 16; caxis([0 1]); colormap jet; hold on gscatter(X(:,1),X(:,2),y,'mc','.x',[15,10]); sv = X(SVMModel.IsSupportVector,:); plot(sv(:,1),sv(:,2),'yo','MarkerSize',15,'LineWidth',2); axis tight hold off

В двухклассном обучении, если классы разделимы, то существует три области: одна, где наблюдения имеют положительную апостериорную вероятность класса 0, тот, где это 1, и другой, где это положительный класс предшествующей вероятности.
Этот пример показывает, как определить, какой квадрант изображения занимает форма, путем настройки модели выходных кодов с исправлением ошибок (ECOC), состоящей из линейных двоичных учащихся SVM. Этот пример также иллюстрирует потребление дискового пространства моделей ECOC, которые хранят векторы поддержки, их метки и предполагаемые коэффициенты.
Создайте набор данных
Случайным образом поместите окружность с радиусом пять в изображение 50 на 50. Сделайте 5000 изображений. Создайте метку для каждого изображения, указывающую квадрант, который занимает круг. Квадрант 1 находится в верхнем правом, квадрант 2 - в верхнем левом, квадрант 3 - в нижнем левом, а квадрант 4 - в нижнем правом. Предикторами являются интенсивности каждого пикселя.
d = 50; % Height and width of the images in pixels n = 5e4; % Sample size X = zeros(n,d^2); % Predictor matrix preallocation Y = zeros(n,1); % Label preallocation theta = 0:(1/d):(2*pi); r = 5; % Circle radius rng(1); % For reproducibility for j = 1:n figmat = zeros(d); % Empty image c = datasample((r + 1):(d - r - 1),2); % Random circle center x = r*cos(theta) + c(1); % Make the circle y = r*sin(theta) + c(2); idx = sub2ind([d d],round(y),round(x)); % Convert to linear indexing figmat(idx) = 1; % Draw the circle X(j,:) = figmat(:); % Store the data Y(j) = (c(2) >= floor(d/2)) + 2*(c(2) < floor(d/2)) + ... (c(1) < floor(d/2)) + ... 2*((c(1) >= floor(d/2)) & (c(2) < floor(d/2))); % Determine the quadrant end
Постройте график наблюдения.
figure imagesc(figmat) h = gca; h.YDir = 'normal'; title(sprintf('Quadrant %d',Y(end)))

Обучение модели ECOC
Используйте 25% -ную выборку и укажите индексы обучения и удержания выборки.
p = 0.25; CVP = cvpartition(Y,'Holdout',p); % Cross-validation data partition isIdx = training(CVP); % Training sample indices oosIdx = test(CVP); % Test sample indices
Создайте шаблон SVM, который задает хранение векторов поддержки двоичных учащихся. Передайте его и обучающие данные в fitcecoc для обучения модели. Определите ошибку классификации обучающей выборки.
t = templateSVM('SaveSupportVectors',true); MdlSV = fitcecoc(X(isIdx,:),Y(isIdx),'Learners',t); isLoss = resubLoss(MdlSV)
isLoss = 0
MdlSV является обученным ClassificationECOC многоклассовая модель. Он хранит обучающие данные и векторы поддержки каждого двоичного учащегося. Для больших наборов данных, таких как в анализе изображений, модель может потреблять много памяти.
Определите объем дискового пространства, используемого моделью ECOC.
infoMdlSV = whos('MdlSV');
mbMdlSV = infoMdlSV.bytes/1.049e6mbMdlSV = 763.6150
Модель потребляет 763,6 МБ.
Повышение эффективности модели
Можно оценить выборочную эффективность. Можно также оценить, была ли модель избыточной с уплотненной моделью, которая не содержит векторов поддержки, их связанных параметров и обучающих данных.
Отбросьте векторы поддержки и связанные параметры из обученной модели ECOC. Затем отбросьте обучающие данные из полученной модели при помощи compact.
Mdl = discardSupportVectors(MdlSV); CMdl = compact(Mdl); info = whos('Mdl','CMdl'); [bytesCMdl,bytesMdl] = info.bytes; memReduction = 1 - [bytesMdl bytesCMdl]/infoMdlSV.bytes
memReduction = 1×2
0.0626 0.9996
В этом случае отказ от векторов поддержки уменьшает потребление памяти примерно на 6%. Уплотнение и сброс поддерживающих векторов уменьшает размер примерно на 99,96%.
Альтернативным способом управления векторами поддержки является уменьшение их количества во время обучения путем определения большего прямоугольного ограничения, такого как 100. Хотя модели SVM, которые используют меньше векторов поддержки, более желательны и потребляют меньше памяти, увеличение значения ограничения коробки имеет тенденцию увеличивать время обучения.
Удаление MdlSV и Mdl из рабочей области.
clear Mdl MdlSV
Оценка эффективности образца Holdout
Вычислите классификационную ошибку выборки удержания. Постройте график выборки предсказаний удержания.
oosLoss = loss(CMdl,X(oosIdx,:),Y(oosIdx))
oosLoss = 0
yHat = predict(CMdl,X(oosIdx,:)); nVec = 1:size(X,1); oosIdx = nVec(oosIdx); figure; for j = 1:9 subplot(3,3,j) imagesc(reshape(X(oosIdx(j),:),[d d])) h = gca; h.YDir = 'normal'; title(sprintf('Quadrant: %d',yHat(j))) end text(-1.33*d,4.5*d + 1,'Predictions','FontSize',17)

Модель не ошибочно классифицирует какие-либо наблюдения выборок удержания.
bayesopt | fitcsvm | kfoldLoss
[1] Хасти, Т., Р. Тибширани и Дж. Фридман. Элементы статистического обучения, второе издание. Нью-Йорк: Спрингер, 2008.
[2] Christianini, N., and J. Shawe-Taylor. Введение в машины опорных векторов и других основанных на ядре методов обучения. Кембридж, Великобритания: Cambridge University Press, 2000.
[3] Вентилятор, R.-E., P.-H. Чен и К.-Ж. Lin. «Работа набора с использованием информации второго порядка для обучения машин опорных векторов». Journal of Машинного обучения Research, Vol 6, 2005, pp. 1889-1918.
[4] Кечман В., Т. -М. Хуан и М. Фогт. Итерационный алгоритм единичных данных для обучения машин ядра из огромных наборов данных: теория и эффективность. В машинах опорных векторов: теория и приложения. Под редакцией Липо Ван, 255-274. Берлин: Springer-Verlag, 2005.