Fiala Wheel 2DOF

Колесо 2DOF Fiala с диском, барабаном или картографическим тормозом

Библиотека:
Динамика автомобиля Blockset/Колеса и шины

Описание

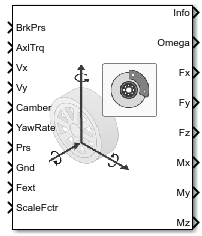
Блок Fiala Wheel 2DOF реализует упрощенную шину с боковой и продольной скольжением на основе модели E. Fiala^[1]. Блок использует поступательную модель трения, чтобы вычислить силы и моменты во время комбинированного продольного и бокового скольжения, требуя меньше параметров, чем Combined Slip Wheel 2DOF блок. Если у вас нет коэффициентов шины, необходимых для Magic Formula, рассмотрите использование этого блока для исследований, которые не включают обширную нелинейную комбинированную боковую скольжение или боковую динамику. Если ваше исследование требует нелинейной комбинированной скольжения или боковой динамики, рассмотрите использование блока Combined Slip Wheel 2DOF.

Блок определяет скорость вращения колеса, вертикальное движение и силы и моменты во всех шести степенях свободы (DOF) на основе крутящего момента привода, тормозного давления, высоты дороги, угла развала колеса и давления надувания. Можно использовать этот блок для следующих типов анализов:

Симуляции привода и транспортного средства, которые требуют низкочастотных шин-дорога и тормозных сил для вычислений транспортного средства ускорения, торможения и сопротивления качению колеса с минимальными параметрами шины.
Взаимодействие колес с идеализированным дорожным покрытием.
Маневры езды и обработки для транспортных средств, проходящих мягкое комбинированное скольжение. Для этого анализа можно подключить блок к приводу и компонентам шасси, таким как дифференциалы, подвеска и системы кузова транспортного средства.
Стабильность рыскания. Для этого анализа можно подключить этот блок к более детальным системным моделям торможения.
Жесткость шины и непрошенное массовое взаимодействие с изменениями заземления, передачей нагрузки или движением шасси с помощью вертикального DOF блока.

Блок интегрирует модели вращательного колеса, вертикальной массы и динамики торможения. Для сил и моментов, зависящих от скольжения, блок реализует модель шины Fiala.

Используйте параметр Brake Type, чтобы выбрать тормоз.

Цель	Настройка типа тормоза
Нет торможения	`None`
Реализуйте тормоз, который преобразует давление в тормозном цилиндре в тормозную силу	`Disc`
Реализуйте симплексный барабанный тормоз, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной крутящий момент	`Drum`
Реализуйте интерполяционную таблицу, которая является функцией скорости и прикладываемого тормозного давления колеса	`Mapped`

Чтобы вычислить крутящий момент сопротивления качению, задайте один из следующих Rolling Resistance параметров.

Настройка	Реализация блока
`None`	Ничего
`Pressure and velocity`	Метод в методике ступенчатого прибрежного бурения для измерения сопротивления качению шин. Сопротивление качению является функцией давления в шине, нормальной силы и скорости.
`ISO 28580`	Метод, указанный в ISO 28580:2018, Метод измерения сопротивления качению легковых, грузовых и автобусных шин - Однофазная точка тест и корреляция результатов измерений.
`Magic Formula`	Магические формульные уравнения из 4.E70 в Tire и Динамику аппарата. Магическая формула является эмпирическим уравнением, основанным на аппроксимационных коэффициентах.
`Mapped torque`	Интерполяционная таблица, которая является функцией от нормальной силы и продольной скорости оси спина.

Чтобы вычислить вертикальное движение, задайте один из следующих Vertical Motion параметров.

Настройка	Реализация блока
`None`	Блок передает приложенные силы шасси непосредственно к вычислениям сопротивления качению и продольной силы.
`Mapped stiffness and damping`	Вертикальное движение зависит от жесткости колеса и демпфирования. Жесткость является функцией перемещения боковой стенки шины и давления. Демпфирование является функцией скорости и давления боковой стенки шины.

Динамика Вращательного Колеса

Блок вычисляет инерционную характеристику колеса, удовлетворяющего:

Потери на оси
Тормозной и приводной крутящий момент
Сопротивление качению шин
Контакт заземления через интерфейс шина-дорога

Входной крутящий момент является суммированием приложенного крутящего момента оси, тормозного момента и момента, возникающего из-за объединенного крутящего момента шины.

$T_{i} = T_{a} - T_{b} + T_{d}$

На момент, вытекающий из комбинированного крутящего момента шины, блок реализует силы тягового колеса и сопротивление качению с динамикой первого порядка. Сопротивление качению имеет постоянную по времени, параметризованную с точки зрения длины релаксации.

$T_{d} (s) = \frac{1}{\frac{| ω | R_{e}}{L_{e}} s + 1} (F_{x} R_{e} + M_{y})$

Чтобы вычислить крутящий момент сопротивления качению, можно задать один из следующих Rolling Resistance параметров.

Настройка	Реализация блока
`None`	Блок устанавливает сопротивление качению, `_My`, в нуль.
`Pressure and velocity`	Блок использует метод в SAE Stepwise Coastdown Methodology для измерения сопротивления качению шин. Сопротивление качению является функцией давления в шине, нормальной силы и скорости. В частности, $M_{y} = R_{e} {a + b \| V_{x} \| + c V_{x}^{2}} {F_{z}^{β} p_{i}^{α}} \tanh (4 V_{x})$
`ISO 28580`	Блок использует метод, указанный в ISO 28580:2018, Метод измерения сопротивления качению легкового автомобиля, грузового автомобиля и автобуса - Однофазная точка тест и корреляция результатов измерений. Метод учитывает нормальную нагрузку, паразитарные потери и тепловые коррекции от условий тестирования. В частности, $M_{y} = R_{e} (\frac{F_{z} C_{r}}{1 + K_{t} (T_{a m b} - T_{m e a s})} - F_{p l}) \tanh (ω)$
`Magic Formula`	Блок вычисляет сопротивление качению, `_My`, используя уравнения Магической Формулы из 4.E70 в Шине и Динамике аппарата. Магическая формула является эмпирическим уравнением, основанным на аппроксимационных коэффициентах.
`Mapped torque`	Для сопротивления качению, `_My`, блок использует интерполяционную таблицу, которая является функцией от нормальной силы и продольной скорости оси вращения.

Если тормоза включены, блок определяет условие блокировки или разблокировки торможения на основе идеализированной модели трения сухой муфты. На основе условия блокировки блок реализует эти модели трения и динамики.

Если	Блокировка Условия	Модель трения	Динамическая модель
$\begin{array}{l} ω \neq 0 \\ или \\ T_{S} < \| T_{i} + T_{f} - ω b \| \end{array}$	Незапертый	$\begin{array}{l} T_{f} = T_{k} \\ где, \\ T_{k} = F_{c} R_{e f f} μ_{k} \tanh [4 (- ω_{d})] \\ T_{s} = F_{c} R_{e f f} μ_{s} \\ R_{e f f} = \frac{2 (R_{o}^{3} - R_{i}^{3})}{3 (R_{o}^{2} - R_{i}^{2})} \end{array}$	$\dot{ω} J = - ω b + T_{i} + T_{o}$
$\begin{array}{l} ω = 0 \\ и \\ T_{S} \geq \| T_{i} + T_{f} - ω b \| \end{array}$	Запертый	$T_{f} = T_{s}$	$ω = 0$

В уравнениях используются эти переменные.

ω	Скорость вращения колеса
a	Независимая от скорости силовой компонент
b	Компонент линейной силы скорости
c	Квадратичная сила скорости компонента
_Le	Длина релаксации шин
J	Момент инерции
_My	Крутящий момент сопротивления качению
_Ta	Приложенный крутящий момент на оси
_Tb	Тормозной крутящий момент
_Td	Комбинированный крутящий момент в шинах
_Tf	Фрикционный крутящий момент
_Ti	Крутящий момент входа сети
_Tk	Кинетический фрикционный крутящий момент
_To	Крутящий момент выхода сети
_Ts	Статический крутящий момент трения
_Fc	Приложенная сила сцепления
_Fx	Продольная сила, развиваемая интерфейсом дороги шины из-за скольжения
_Reff	Эффективный радиус сцепления
_Ro	Внешний радиус кольцевого диска
_Ri	Внутренний радиус кольцевого диска
_Re	Эффективный радиус шины при нагрузке и при заданном давлении
_Vx	Скорость продольной оси
_Fz	Нормальная сила транспортного средства
_Cr	Постоянное сопротивление качению
_Tamb	Температура окружающей среды
_Tmeas	Измеренная температура для постоянного сопротивления качению
_Fpl	Потеря паразитной силы
_Kt	Коэффициент тепловой коррекции
ɑ	Экспонента давления в шинах
β	Нормальная экспонента силы
_pi	Давление в шинах
_μs	Коэффициент статического трения
_μk	Коэффициент кинетического трения

Продольная Сила

Блок реализует продольную силу как функцию скольжения колеса относительно поверхности дороги, используя эти уравнения.

Вычисление	Уравнение
Критический скольжение	$κ'_{C r i t i c a l} = \| \frac{μ F_{z}}{2 C_{κ}} \|$
Продольная сила	$F_{x} = {\begin{matrix} C_{k} κ' when \| κ^{'} \| \leq κ^{'}_{C r i t i c a l} \\ tanh (4 κ') (μ \| F_{z} \| - \| \frac{{(μ F_{z})}^{2}}{4 κ' C_{κ}} \|) когда \| κ^{'} \| > κ^{'}_{C r i t i c a l} \end{matrix}$
Коэффициент трения	$μ = (μ_{s} - (μ_{s} - μ_{k}) κ_{k α}) λ_{μ}$
Коэффициент скольжения	$κ_{k α} = \sqrt{κ'^{2} + {tan}^{2} (α')}$

В уравнениях используются эти переменные.

κ'	Скольжение по состоянию
_Fx	Продольная сила, действующая на ось вдоль фиксированной по оси X шины,
_Cκ	Продольная жесткость
_Fz	Вертикальная контактная закрашенная фигура нормальной силы вдоль фиксированной оси Z шины,
μ	Коэффициент трения
_μs	Коэффициент статического трения
_μk	Коэффициент кинетического трения
_κka	Комплексный коэффициент скольжения
α'	Состояние угла скольжения
_λμ	Масштабирование трения

Боковая Сила

Блок реализует боковую силу как функцию от состояния угла скольжения колеса, используя эти уравнения.

Вычисление	Уравнение
Критический угол скольжения	$α'_{C r i t i c a l} = atan (\frac{3 μ \| F_{z} \|}{C_{a}})$
Боковая сила	$\begin{array}{l} F_{y} = {\begin{matrix} - tanh (4 α') μ \| F_{z} \| когда \| α' \| > α'_{C r i t i c a l} \\ - \tanh (4 α') μ \| F_{z} \| (1 - ξ^{3}) + γ C_{γ} когда \| α' \| \leq α'_{C r i t i c a l} \end{matrix} \\ ξ = 1 - \frac{C_{a} \| tan (α') \|}{3 μ \| F_{z} \|} \end{array}$

В уравнениях используются эти переменные.

α'	Состояние угла скольжения
_Fy	Боковая сила, действующая на ось вдоль фиксированной по оси Y шины,
_Fz	Вертикальная контактная закрашенная фигура нормальной силы вдоль фиксированной оси Z шины
_Cɣ	Жесткость развала
_Cα	Боковая жесткость на угол скольжения
μ	Коэффициент трения

Вертикальная динамика

Для вертикальной динамики блок реализует эти уравнения.

Вычисление	Уравнение
Вертикальная характеристика	$\ddot{z} m = F_{z t i r e} + m g - F z$
Нормальная сила шины	$F_{z t i r e} = ρ_{z} k - b \dot{z}$
Вертикальное отклонение боковой стенки	$ρ_{z} = z_{g n d} - z, z \geq 0$

В уравнениях используются эти переменные.

z	Отклонение шины вдоль фиксированной оси Z
_zgnd	Перемещение заземления вдоль неподвижной z -оси шины
_Fztire	Нормальное усилие шины вдоль фиксированной оси Z
_Fz	Вертикальная сила, действующая на ось вдоль неподвижной оси Z шины
_ρz	Вертикальное отклонение боковой стенки вдоль фиксированной по оси Z шины
k	Вертикальная жесткость боковой стенки
b	Демпфирование вертикальной боковой стенки

Опрокидывание, выравнивание и масштабирование

В этой таблице результирующая реализация опрокидывания, выравнивания и масштабирования.

Вычисление Реализация

Вычисление	Реализация
Опрокидывающий момент	Модель Фиала не задает опрокидывающий момент. Блок реализует это уравнение, требуя минимальных параметров. $M_{x} = F_{y} R_{e} cos (γ)$
Выравнивающий момент	Блок реализует выравнивающий момент как комбинацию демпфирования скорости рыскания и состояния угла скольжения. $\begin{array}{l} M_{z} = {\begin{matrix} \dot{ψ} b_{M_{z}} когда \| α' \| > α'_{C r i t i c a l} \\ \tanh (4 α^{'}) w μ \| F_{z} \| (1 - ξ) ξ^{3} + \dot{ψ} b_{M_{z}} когда \| α' \| \leq α'_{C r i t i c a l} \end{matrix} \\ ξ = 1 - \frac{C_{a} \| tan (α') \|}{3 μ \| F_{z} \|} \end{array}$
Масштабирование трения	Чтобы изменить коэффициент трения, используйте `ScaleFctr` входной порт.

Опрокидывающий момент

Модель Фиала не задает опрокидывающий момент. Блок реализует это уравнение, требуя минимальных параметров.

$M_{x} = F_{y} R_{e} cos (γ)$

Выравнивающий момент

Блок реализует выравнивающий момент как комбинацию демпфирования скорости рыскания и состояния угла скольжения.

$\begin{array}{l} M_{z} = {\begin{matrix} \dot{ψ} b_{M_{z}} когда | α' | > α'_{C r i t i c a l} \\ \tanh (4 α^{'}) w μ | F_{z} | (1 - ξ) ξ^{3} + \dot{ψ} b_{M_{z}} когда | α' | \leq α'_{C r i t i c a l} \end{matrix} \\ ξ = 1 - \frac{C_{a} | tan (α') |}{3 μ | F_{z} |} \end{array}$

Масштабирование трения

Чтобы изменить коэффициент трения, используйте ScaleFctr входной порт.

В уравнениях используются эти переменные.

_Mx	Опрокидывающий момент, действующий на ось вокруг фиксированной по оси X шины
_Mz	Выравнивающий момент, действующий на ось вокруг неподвижной оси Z шины
_Re	Эффективная контактная закрашенная фигура к радиальному расстоянию носителя колеса
ɣ	Угол развала
k	Вертикальная жесткость боковой стенки
b	Демпфирование вертикальной боковой стенки
$\dot{ψ}$	Скорость вращения шины вокруг фиксированной в шине оси Z (скорость рыскания)
w	Ширина шины
α'	Состояние угла скольжения
_bMz	Сопротивление линейной скорости рыскания
_Fy	Боковая сила, действующая на ось вдоль фиксированной по оси Y шины
_Cɣ	Жесткость развала
_Cα	Боковая жесткость на угол скольжения
μ	Коэффициент трения
_Fz	Вертикальная контактная закрашенная фигура нормальной силы вдоль фиксированной оси Z шины

Системы координат шин и колес

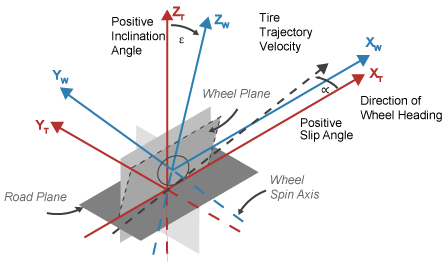
Чтобы разрешить силы и моменты, блок использует ориентацию Z-Up для систем координат шины и колеса.

Оси систем координат шин (_XT, _YT, _ZT) фиксируются в опорной системе координат, присоединенной к шине. Источник находится в контакте шины с землей.
Оси системы координат колеса (_XW, _YW, _ZW) фиксируются в опорной раме, прикрепленной к колесу. Источник находится в центре колеса.

Ориентация по оси Z^[1]

Z-Up tire and wheel coordinate systems showing wheel plane and road plane

Тормоза

Диск

Если вы задаете параметр Brake Type Discблок реализует дисковый тормоз. Этот рисунок показывает вид сбоку и спереди дискового тормоза.

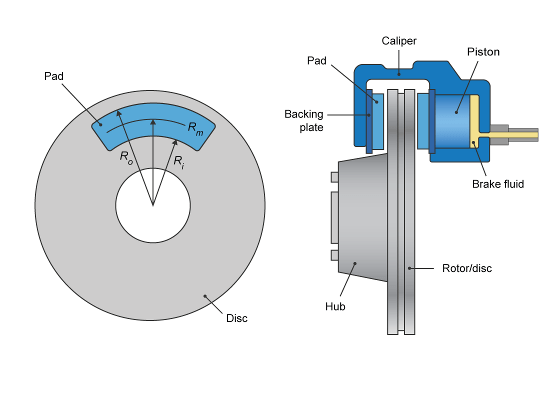
Front and side view of disc brake, showing pad, disc, and caliper

Дисковый тормоз преобразует давление в тормозном цилиндре из тормозного цилиндра в усилие. Дисковый тормоз прикладывает силу к среднему радиусу тормозной колодки.

Блок использует эти уравнения, чтобы вычислить момент привода для дискового тормоза.

$T = {\begin{matrix} \frac{μ P π B_{a}^{2} R_{m} N_{p a d s}}{4} когда N \neq 0 \\ \frac{μ_{s t a t i c} P π B_{a}^{2} R_{m} N_{p a d s}}{4} когда N = 0 \end{matrix}$

$R m = \frac{R o + R i}{2}$

В уравнениях используются эти переменные.

T	Момент привода
P	Прикладываемое тормозное давление
N	Скорость колеса
_Npads	Количество тормозных колодок в узле дискового тормоза
_μstatic	Коэффициент статического трения пары диск-колодка
μ	Коэффициент кинетического трения пары диск-колодка
_Ba	Внутренний диаметр тормозного цилиндра суппорта
_Rm	Средний радиус приложения силы тормозной колодки на роторе тормоза
_Ro	Внешний радиус тормозной колодки
_Ri	Внутренний радиус тормозной колодки

Барабан

Если вы задаете параметр Brake Type Drum, блок реализует статический (статический) симплексный барабанный тормоз. Симплексный барабанный тормоз состоит из одного двустороннего гидравлического привода и двух тормозных колодок. Тормозные колодки не имеют общего шарнирного контакта.

Модель симплексного барабанного тормоза использует приложенную силу и геометрию тормоза, чтобы вычислить крутящий момент привода для каждой тормозной колодки. Модель барабана принимает, что приводы и геометрия башмака симметричны для обеих сторон, позволяя использовать один набор геометрии и параметров трения для обеих башмаков.

Блок реализует уравнения, которые получают из этих уравнений в Основах Элементов Машины.

$\begin{array}{l} T_{r s h o e} = (\frac{π μ c r (\cos θ_{2} - \cos θ_{1}) B_{a}^{2}}{2 μ (2 r (\cos θ_{2} - \cos θ_{1}) + a (\cos^{2} θ_{2} - \cos^{2} θ_{1})) + a r (2 θ_{1} - 2 θ_{2} + \sin 2 θ_{2} - \sin 2 θ_{1})}) P \\ T_{l s h o e} = (\frac{π μ c r (\cos θ_{2} - \cos θ_{1}) B_{a}^{2}}{- 2 μ (2 r (\cos θ_{2} - \cos θ_{1}) + a (\cos^{2} θ_{2} - \cos^{2} θ_{1})) + a r (2 θ_{1} - 2 θ_{2} + \sin 2 θ_{2} - \sin 2 θ_{1})}) P \end{array}$

$T = {\begin{matrix} T_{r s h o e} + T_{l s h o e} when N \neq 0 \\ (T_{r s h o e} + T_{l s h o e}) \frac{μ_{s t a t i c}}{μ} когда N = 0 \end{matrix}$

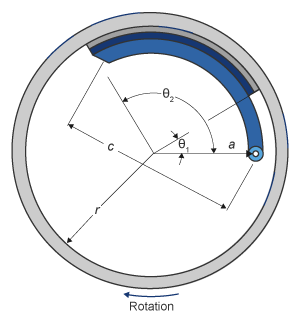
Side view of drum brake

В уравнениях используются эти переменные.

T	Момент привода
P	Прикладываемое тормозное давление
N	Скорость колеса
_μstatic	Коэффициент статического трения пары диск-колодка
μ	Коэффициент кинетического трения пары диск-колодка
_Trshoe	Момент привода правой колодки
_Tlshoe	Момент привода левой колодки
a	Расстояние от центра барабана до шарнира контакта центра башмака
c	Расстояние от шарнира контакта центра колодки до соединения привода тормоза на колодке тормоза
r	Внутренний радиус барабана
_Ba	Внутренний диаметр тормозного цилиндра суппорта
_Θ1	Угол от шарнира контакта центра колодки до начала материала тормозной колодки на колодке
_Θ2	Угол от шарнира контакта центра к концу материала тормозной колодки на колодке

Нанесенный на карту

Если вы задаете параметр Brake Type Mappedблок использует интерполяционную таблицу, чтобы определить момент привода.

$T = {\begin{matrix} f_{b r a k e} (P, N) when N \neq 0 \\ (\frac{μ_{s t a t i c}}{μ}) f_{b r a k e} (P, N) когда N = 0 \end{matrix}$

В уравнениях используются эти переменные.

T	Момент привода
$f_{b r a k e}^{} (P, N)$	Интерполяционная таблица момента привода
P	Прикладываемое тормозное давление
N	Скорость колеса
_μstatic	Коэффициент трения интерфейса «поверхность-поверхность барабана» при статических условиях
μ	Коэффициент трения интерфейса диск-ротор

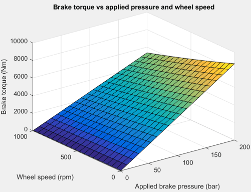
Интерполяционная таблица для крутящего момента привода, $f_{b r a k e}^{} (P, N)$ , является функцией прикладываемого тормозного давления и скорости вращения колеса, где:

T - момент привода, в Н· м.
P прикладываемого тормозного давления, в баре.
N - скорость колеса, в об/мин.

Plot of brake torque as a function of wheel speed and applied brake pressure

Порты

Вход

расширить все

`BrkPrs` - Давление торможения
`scalar` | `N`-by- `1` вектор

Давление торможения, в Па.

Вектор - это количество колес, N, по 1. Если вы задаете скалярное значение, блок принимает, что количество колес равно единице.

Зависимости

Чтобы включить этот порт, для параметра Brake Type задайте один из следующих типов:

Disc
Drum
Mapped

`AxlTrq` - Крутящий момент на оси
`scalar` | `N`-by- `1` вектор

Крутящий момент оси, _Ta, вокруг оси вращения колеса, в Н· м.

`Vx` - Продольная скорость
`scalar` | `N`-by- `1` вектор

Продольная скорость оси, _Vx, вдоль фиксированной по оси X, в м/с.

`Vy` - Поперечная скорость
`scalar` | `N`-by- `1` вектор

Поперечная скорость оси, _Vy, вдоль фиксированной по оси Y шины, в м/с.

`Camber` - Угол развала
`scalar` | `N`-by- `1` вектор

Угол развала, ɣ, в рад.

`YawRate` - скорость вращения шины
`scalar` | `N`-by- `1` вектор

Скорость вращения шины, r, вокруг фиксированной в шине оси Z (скорость рыскания), в рад/с.

`Prs` - Давление наддува шин
`scalar` | `N`-by- `1` вектор

Давление инфляции в шинах, _pi, в Па.

`Gnd` - Перемещение грунта
`scalar` | `N`-by- `1` вектор

Перемещение заземления вдоль неподвижной z оси, в м. Положительный вход обеспечивает подъем колеса.

`Fext` - Сила оси, приложенная к шине
`scalar` | `N`-by- `1` вектор

Сила оси, приложенная к шине, _Fext, вдоль фиксированной осей Z автомобиля (положительный вход сжимает шину), в Н.

`ScaleFctrs` - Масштабный коэффициент
`scalar` | `N`-by- `1` вектор

Масштабный коэффициент для расчета изменений коэффициента трения.

Выход

расширить все

`Info` - Блочные данные
автобус

Блочные данные, возвращенные как сигнал шины, содержащий эти значения блоков.

Сигнал	Описание	Модули
`AxlTrq`	Крутящий момент оси вокруг неподвижной оси Y	Н· м
`Omega`	Скорость вращения колеса вокруг фиксированной по оси Y колеса	рад/с
`Fx`	Продольная сила транспортного средства вдоль фиксированной по оси X шины	N
`Fy`	Боковая сила транспортного средства вдоль фиксированной по оси Y шины	N
`Fz`	Вертикальное усилие транспортного средства вдоль фиксированной по оси Z шины	N
`Mx`	Опрокидывающий момент вокруг фиксированной по оси X шины	Н· м
`My`	Крутящий момент сопротивления качению вокруг фиксированной по оси Y шины	Н· м
`Mz`	Выравнивающий момент вокруг фиксированной по оси Z шины	Н· м
`Vx`	Продольная скорость транспортного средства вдоль фиксированной по оси X шины	м/с
`Vy`	Поперечная скорость транспортного средства вдоль фиксированной по оси Y шины	м/с
`Re`	Нагруженный эффективный радиус	m
`Kappa`	Отношение продольных скольжений	НА
`Alpha`	Угол скольжения по стороне	рад
`a`	Контактная закрашенная фигура половинной длины	m
`b`	Контакт с закрашенной фигурой половинной ширины	m
`Gamma`	Угол развала	рад
`psidot`	Скорость вращения шины вокруг фиксированной в шине оси Z (скорость рыскания)	рад/с
`BrkTrq`	Момент привода вокруг фиксированной по оси Y автомобиля	Н· м
`BrkPrs`	Давление торможения	Pa
`z`	Вертикальное перемещение оси вдоль фиксированной оси Z шины	m
`zdot`	Вертикальная скорость оси вдоль фиксированной оси Z шины	м/с
`Gnd`	Перемещение заземления вдоль фиксированной по оси Z шины (положительный вход создает подъем колеса)	m
`GndFz`	Вертикальное усилие боковой стенки на земле вдоль неподвижной оси Z шины	N
`Prs`	Давление надувания шин	Pa

`Omega` - скорость вращения колеса
`scalar` | `N`-by- `1` вектор

Скорость вращения колеса, ω, вокруг фиксированной по оси Y, в рад/с.

`Fx` - Сила продольной оси
`scalar` | `N`-by- `1` вектор

Продольная сила, действующая на ось, _Fx, вдоль фиксированной по оси X шины, в Н. Положительная сила, действующая на перемещение транспортного средства вперед.

`Fy` - Боковая осевая сила
`scalar` | `N`-by- `1` вектор

Боковая сила, действующая на ось, _Fy, вдоль фиксированной по оси Y шины, в Н.

`Fz` - Вертикальная осевая сила
`scalar` | `N`-by- `1` вектор

Вертикальная сила, действующая на ось, _Fz, вдоль фиксированной в шине оси Z, в Н.

`Mx` - Опрокидывающий момент
`scalar` | `N`-by- `1` вектор

Продольный момент, действующий на ось, _Mx, вокруг оси X шины, в N· м.

`My` - Момент сопротивления качению
`scalar` | `N`-by- `1` вектор

Боковой момент, действующий на ось, _My, вокруг оси Y шины, в Н· м.

`Mz` - Выравнивающий момент
`scalar` | `N`-by- `1` вектор

Вертикальный момент, действующий на ось, _Mz, вокруг оси Z шины, в Н· м.

Параметры

расширить все

Опции блока

`Brake Type` - Выбор типа
`None` | `Disc` | `Drum` | `Mapped`

Используйте параметр Brake Type, чтобы выбрать тормоз.

Цель	Настройка типа тормоза
Нет торможения	`None`
Реализуйте тормоз, который преобразует давление в тормозном цилиндре в тормозную силу	`Disc`
Реализуйте симплексный барабанный тормоз, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной крутящий момент	`Drum`
Реализуйте интерполяционную таблицу, которая является функцией скорости и прикладываемого тормозного давления колеса	`Mapped`

`Rolling Resistance` - Выбор типа
`None` (по умолчанию) | `Pressure and velocity` | `ISO 28580` | `Magic Formula` | `Mapped torque`

Чтобы вычислить крутящий момент сопротивления качению, задайте один из следующих Rolling Resistance параметров.

Настройка	Реализация блока
`None`	Ничего
`Pressure and velocity`	Метод в методике ступенчатого прибрежного бурения для измерения сопротивления качению шин. Сопротивление качению является функцией давления в шине, нормальной силы и скорости.
`ISO 28580`	Метод, указанный в ISO 28580:2018, Метод измерения сопротивления качению легковых, грузовых и автобусных шин - Однофазная точка тест и корреляция результатов измерений.
`Magic Formula`	Магические формульные уравнения из 4.E70 в Tire и Динамику аппарата. Магическая формула является эмпирическим уравнением, основанным на аппроксимационных коэффициентах.
`Mapped torque`	Интерполяционная таблица, которая является функцией от нормальной силы и продольной скорости оси спина.

Зависимости

Выбор	Параметры
`Pressure and velocity`	Velocity independent force coefficient, aMy Linear velocity force component, bMy Quadratic velocity force component, cMy Tire pressure exponent, alphaMy Normal force exponent, betaMy
`ISO 28580`	Parasitic losses force, Fpl Rolling resistance constant, Cr Thermal correction factor, Kt Measured temperature, Tmeas Parasitic losses force, Fpl Ambient temperature, Tamb
`Magic Formula`	Rolling resistance torque coefficient, QSY Longitudinal force rolling resistance coefficient, QSY2 Linear rotational speed rolling resistance coefficient, QSY3 Quartic rotational speed rolling resistance coefficient, QSY4 Camber squared rolling resistance torque, QSY5 Load based camber squared rolling resistance torque, QSY6 Normal load rolling resistance coefficient, QSY7 Pressure load rolling resistance coefficient, QSY8 Rolling resistance scaling factor, lam_My
`Mapped torque`	Spin axis velocity breakpoints, VxMy Normal force breakpoints, FzMy Rolling resistance torque map, MyMap

`Vertical Motion` - Выбор типа
`None` (по умолчанию) | `Mapped stiffness and damping`

Чтобы вычислить вертикальное движение, задайте один из следующих Vertical Motion параметров.

Настройка	Реализация блока
`None`	Блок передает приложенные силы шасси непосредственно к вычислениям сопротивления качению и продольной силы.
`Mapped stiffness and damping`	Вертикальное движение зависит от жесткости колеса и демпфирования. Жесткость является функцией перемещения боковой стенки шины и давления. Демпфирование является функцией скорости и давления боковой стенки шины.

Выбор Включает эти параметры

Выбор	Включает эти параметры
`Mapped stiffness and damping`	Wheel mass, MASS Initial tire displacement, zo Initial velocity, zdoto Initial wheel vertical velocity (wheel fixed frame), zdoto Vertical deflection breakpoints, zFz Pressure breakpoints, pFz Force due to deflection, Fzz Vertical velocity breakpoints, zdotFz Force due to velocity, Fzzdot

Mapped stiffness and damping

Wheel mass, MASS

Initial tire displacement, zo

Initial velocity, zdoto

Initial wheel vertical velocity (wheel fixed frame), zdoto

Vertical deflection breakpoints, zFz

Pressure breakpoints, pFz

Force due to deflection, Fzz

Vertical velocity breakpoints, zdotFz

Force due to velocity, Fzzdot

Продольный и боковой

`Longitudinal stiffness, Ckappa` - Продольная жесткость
`1e7` (по умолчанию) | `scalar`

Продольная жесткость, _Cκ, в Н.

`Lateral stiffness per slip angle, Calpha` - Боковая жесткость
`4.5e4` (по умолчанию) | `scalar`

Боковая жесткость на угол скольжения, _Cα, в Н/рад.

`Camber stiffness, Cgamma` - Жесткость развала
`1e3` (по умолчанию) | `scalar`

Жесткость развала, _Cɣ, в Н/рад.

`Kinematic friction, muMin` - Трение
`.8` (по умолчанию) | `scalar`

Кинематическое трение, _μk, безразмерное.

`Static friction, muMax` - Трение
`1` (по умолчанию) | `scalar`

Статическое трение, _μs, безразмерное.

`Longitudinal relaxation length, Lrelx` - Длина
`.05` (по умолчанию) | `scalar`

Продольная длина расслабления, _Lrelx, в м.

`Lateral relaxation length, Lrely` - Длина
`.15` (по умолчанию) | `scalar`

Длина бокового расслабления, _Lrely, в м/рад.

Вращение

`Rotational damping, br` - Демпфирование
`1e-3` (по умолчанию) | `scalar`

Вращательное демпфирование, br, в Н· м· с/рад.

`Rotational inertia (rolling axis), IYY` - Инерция
`0.74` (по умолчанию) | `scalar`

Инерция вращения (ось качения), IYY, в кг· м ^ 2.

`Initial rotational velocity, omegao` - Скорость
`0` (по умолчанию) | `scalar`

Начальная скорость вращения, в рад/с.

`Unloaded radius, UNLOADED_RADIUS` - Радиус
`0.309384029954441` (по умолчанию) | `scalar`

Радиус разгрузки, в м.

Давление и скорость

`Velocity independent force coefficient, aMy` - Коэффициент силы
`8e-4` (по умолчанию) | `scalar`

Независимый от скорости коэффициент силы, a, в с/м.

Зависимости

Чтобы создать этот параметр, выберите параметр Rolling Resistance Pressure and velocity.

`Linear velocity force component, bMy` - Компонент силы
`.001` (по умолчанию) | `scalar`

Линейный компонент силы скорости, b, в с/м.

Зависимости

Чтобы создать этот параметр, выберите параметр Rolling Resistance Pressure and velocity.

`Quadratic velocity force component, cMy` - Компонент силы
`1.6e-4` (по умолчанию) | `scalar`

Квадратичная сила скорости компонента, c, в с ^ 2/м ^ 2.

Зависимости

Чтобы создать этот параметр, выберите параметр Rolling Resistance Pressure and velocity.

`Tire pressure exponent, alphaMy` - Экспонента давления
`-0.003` (по умолчанию) | `scalar`

Экспонента давления в шине, ɑ, безразмерная.

Зависимости

Чтобы создать этот параметр, выберите параметр Rolling Resistance Pressure and velocity.

`Normal force exponent, betaMy` - Экспонента силы
`0.97` (по умолчанию) | `scalar`

Нормальная экспонента силы, β, безразмерная.

Зависимости

Чтобы создать этот параметр, выберите параметр Rolling Resistance Pressure and velocity.

ISO 28580

`Parasitic losses force, Fpl` - Потеря сил
`10` (по умолчанию) | `scalar`

Потеря паразитической силы, _Fpl, в Н.

Зависимости

Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.

`Rolling resistance constant, Cr` - Константа
`1e-3` (по умолчанию) | `scalar`

Постоянное сопротивление качению, _Cr, в Н/кН. ISO 28580 определяет модуль сопротивления качению как один ньютон тягового сопротивления для каждого килоньютона нормальной нагрузки.

Зависимости

Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.

`Thermal correction factor, Kt` - Коэффициент коррекции
`.008` (по умолчанию) | `scalar`

Коэффициент тепловой коррекции, _Kt, в 1/degC.

Зависимости

Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.

`Measured temperature, Tmeas` - Температура
`298.15` (по умолчанию) | `scalar`

Измеренная температура, _Tmeas, в К.

Зависимости

Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.

`Ambient temperature, Tamb` - Температура
`298.15` (по умолчанию) | `scalar`

Измеренная температура, _Tamb, в К.

Зависимости

Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.

`Input ambient temperature` - Выбор
`off` (по умолчанию) | `on`

Выберите, чтобы создать входной порт Tamb.

Зависимости

Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.

Магическая формула