Geometric camera calibration, также называемый camera resectioning, оценивает параметры объектива и датчика изображения или видеокамеры. Можно использовать эти параметры для исправления искажений объектива, измерения размера объекта в мировых единицах измерения или определения местоположения камеры в сцене. Эти задачи используются в таких приложениях, как машинное зрение, для обнаружения и измерения объектов. Они также используются в робототехнике, для навигационных систем и 3-D реконструкции сцены.
Примеры того, что можно сделать после калибровки камеры:

Параметры камеры включают встроенные, внешние и коэффициенты искажения. Чтобы оценить параметры камеры, необходимо иметь 3-D мировых точек и соответствующих им 2-D точек изображения. Можно получить эти соответствия с помощью нескольких изображений калибровочного шаблона, такого как шахматная доска. Используя соответствия, можно решить для параметров камеры. После калибровки камеры, чтобы оценить точность предполагаемых параметров, можно:
Постройте график относительных местоположений камеры и калибровочного шаблона
Вычислите ошибки репроекции.
Вычислите ошибки расчета параметра.
Используйте Camera Calibrator, чтобы выполнить калибровку камеры и оценить точность предполагаемых параметров.
Computer Vision Toolbox™ содержит алгоритмы калибровки для модели камеры pinhole и модели fisheye-камеры. Можно использовать модель «рыбий глаз» с камерами до поля зрения ( FOV) 195 степеней.
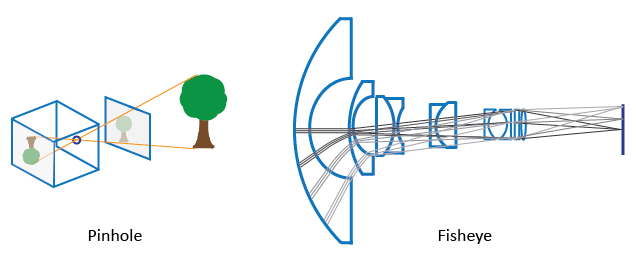
Алгоритм калибровки pinhole основан на модели, предложенной Жан-Ивом Буге [3]. Модель включает, модель камеры pinhole [1] и искажение объектива [2]. Модель камеры pinhole не учитывает искажение объектива, потому что идеальная камера pinhole не имеет объектива. Чтобы точно представлять реальную камеру, полная модель камеры, используемая алгоритмом, включает радиальное и тангенциальное искажение объектива.
Из-за экстремальных искажений, которые производит линза «рыбий глаз», модель pinhole не может смоделировать fisheye-камеры. Для получения дополнительной информации о калибровке камеры с помощью модели «рыбий глаз» см. «Основы калибровки» рыбий глаз «».
Камера pinhole представляет собой простую камеру без объектива и с одинарной небольшой апертурой. Световые лучи проходят через апертуру и проецируют инвертированное изображение на противоположную сторону камеры. Представьте виртуальную плоскость изображения как находящуюся перед камерой и содержащую вертикальное изображение сцены.
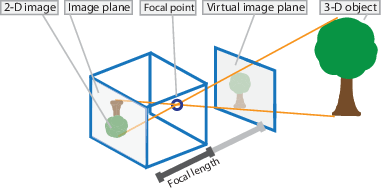
Параметры камеры pinhole представлены в матрице 4 на 3, называемой camera matrix. Эта матрица отображает сцену 3-D мира в плоскость изображения. Алгоритм калибровки вычисляет матрицу камеры с помощью внешних и внутренних параметров. Внешние параметры представляют расположение камеры в 3-D сцене. Собственные параметры представляют оптический центр и фокусное расстояние камеры.
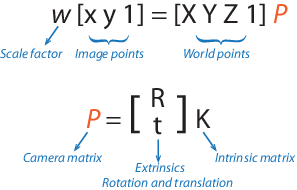
Мировые точки преобразуются в координаты камеры с помощью параметров extinsics. Координаты камеры отображаются в плоскость изображения с помощью собственных параметров.
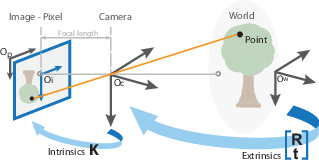
Алгоритм калибровки вычисляет матрицу камеры с помощью внешних и внутренних параметров. Внешние параметры представляют твердое преобразование из мировой системы координат 3-D систему координат 3-D камеры. Внутренние параметры представляют проективное преобразование из координат 3-D камеры в 2-D координаты изображения.
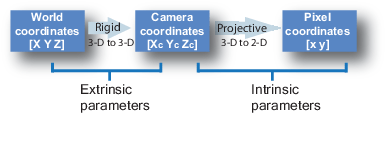
Внешние параметры состоят из вращения, R и перемещения, t. Источник системы координат камеры находится в ее оптическом центре, и ее x- и y- ось определяют плоскость изображения.

Внутренние параметры включают фокусное расстояние, оптический центр, также известный как principal point, и коэффициент наклона. Внутренняя матрица камеры, K, определяется как:
Наклон пикселя определяется как:
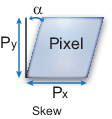
| - Оптический центр (главная точка), в пикселях. |
| - Фокусное расстояние в пикселях. - Фокусное расстояние в мировых единицах измерения, обычно выраженное в миллиметрах. - Размер пикселя в мировых единицах измерения. |
| - Коэффициент наклона, который не равен нулю, если оси изображения не перпендикулярны. |
Матрица камеры не учитывает искажения объектива, потому что идеальная камера pinhole не имеет объектива. Чтобы точно представлять реальную камеру, модель камеры включает радиальное и тангенциальное искажение объектива.
Радиальное искажение происходит, когда световые лучи изгибаются больше около ребер линзы, чем в ее оптическом центре. Чем меньше линза, тем больше искажение.

Коэффициенты радиального искажения моделируют этот тип искажения. Искаженные точки обозначаются как (x искаженные, y искаженные ):
x искаженный = x (1 + k 1 * r2 + <reservedrangesplaceholder1> 2* r4 + <reservedrangesplaceholder1> 3* r6)
y искаженный = y (1 + k 1 * r2 + <reservedrangesplaceholder1> 2* r4 + <reservedrangesplaceholder1> 3* r6)
x, y - неискаженные пиксельные местоположения. x и y находятся в нормированных координатах изображения. Нормированные координаты изображения вычисляются из пиксельных координат путем перевода в оптический центр и деления на фокусное расстояние в пикселях. Таким образом, x и y безразмерны.
k 1, k 2 и k 3 - Коэффициенты радиального искажения объектива.
r2: x2 + y2
Обычно для калибровки достаточно двух коэффициентов. Для серьезных искажений, таких как в широкоугольных объективах, можно выбрать 3 коэффициенты, чтобы включить k 3 .
Тангенциальное искажение происходит, когда линза и плоскость изображения не параллельны. Коэффициенты тангенциального искажения моделируют этот тип искажения.
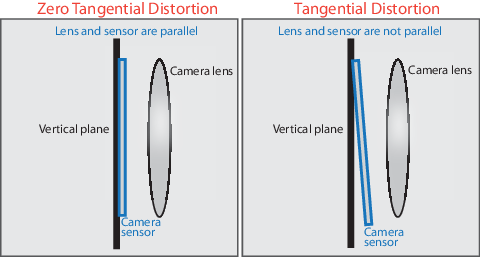
Искаженные точки обозначаются как (x искаженные, y искаженные ):
x искаженный = x + [2 * p 1 * x * y + p 2 * (r2 + 2 * x2)]
y искаженный = y + [p 1 * (r2 + 2 * y2) + 2 * <reservedrangesplaceholder2> 2 * x * y]
x, y - неискаженные пиксельные местоположения. x и y находятся в нормированных координатах изображения. Нормированные координаты изображения вычисляются из пиксельных координат путем перевода в оптический центр и деления на фокусное расстояние в пикселях. Таким образом, x и y безразмерны.
p 1 и p 2 - Коэффициенты тангенциального искажения объектива.
r2: x2 + y2
[1] Чжан, З. «Гибкий новый техник калибровки камеры». Транзакции IEEE по шаблонному анализу и машинному анализу. Том 22, № 11, 2000, стр. 1330-1334.
[2] Heikkila, J., and O. Silven. «Четырехэтапная процедура калибровки камеры с неявной коррекцией изображения». IEEE International Conference on Компьютерное Зрение and Pattern Recognition.1997.
[3] Bouguet, J. Y. «Camera Calibration Toolbox for Matlab». Вычислительное видение в Калифорнийском технологическом институте. Калибровочный Тулбокс камеры для MATLAB
[4] Брадски, Г. и А. Келер. Обучение OpenCV: Компьютерное зрение с библиотекой OpenCV. Sebastopol, CA: O'Reilly, 2008.