Нестационарные системы координат Габора и преобразование Константа-Q

Нестационарные системы координат Габора позволяют вам реализовать адаптивный к времени или частотно-адаптивный анализ сигналов. Функции cqt и icqt используйте нестационарные системы координат Габора, чтобы получить постоянное Q (частотно-адаптивное) преобразование (CQT) сигнала. Заметная сила нестационарных систем координат Габора заключается в том, что они позволяют создавать стабильные обратные системы, что дает идеальную реконструкцию.

Теория нестационарных систем координат Габора и эффективные алгоритмы их реализации обусловлены Dörfler, Holighaus, Grill и Velasco [1][2]. Алгоритмы в [1] и [2] реализуют фазовую автоподстройку CQT, которая не сохраняет те же фазы, которые были бы получены наивной сверткой. В [3] Шёркхубер, Клапури, Холигхаус и Дёрфлер разрабатывают эффективные алгоритмы для CQT и обратной CQT, которые имитируют коэффициенты, полученные наивной сверткой. Large Time-Frequency Analysis Toolbox [4] предоставляет обширный набор алгоритмов для нестационарного анализа и синтеза Габора.

В стандартном анализе Габора окно фиксированного размера облицовывает частотно-временную плоскость. Нестационарная система координат Габора является набором оконных функций различных размеров, которые используются для мозаики частотно-временной плоскости. Вейвлет мозаичит частотно-временную плоскость аналогичным образом. У вас есть гибкость, чтобы изменить плотность дискретизации во времени или частоте. Нестационарные системы координат Габора применяются в областях, таких как обработка аудиосигнала, где фиксированные временные окна частоты не оптимальны. В отличие от краткосрочного преобразования Фурье, окна, используемые в преобразовании constant-Q, имеют адаптируемую полосу пропускания и плотность дискретизации. В разносе частот окна центрируются на логарифмически разнесенных центральных частотах.

Разложение частотно-временной плоскости

Преобразование Фурье f (t) является корреляцией f (t) с e^{j ω t}:

$F (ω) = \int_{- \infty}^{\infty} f (t) e^{- j ω t} d t .$

Начиная с e^{j ω t} не имеет компактной поддержки, преобразование Фурье не является идеальным выбором для изучения нестационарных сигналов. Если содержимое частоты сигнала изменяется с течением времени, преобразование Фурье не захватывает, каковы эти изменения или когда эти изменения происходят. Разбиение частотно-временной плоскости, показанное здесь, представляет это поведение преобразования Фурье.

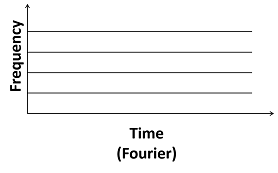
Чтобы выполнить частотно-временной анализ нестационарного сигнала, начните с действительной четной функции оконной обработки, $g (t)$ , которая фактически ненулевая только конечный интервал и имеет норму, равную единице. В сложение преобразование Фурье $g (t)$ центрирован в нуле и является lowpass. Далее окно f (t) с переводами $g (t)$ . Затем примите преобразование Фурье результата

$S F (u, ζ) = \int f (t) g (t - u) e^{- j ζ t} d t .$

Корреляция f (t) с атомами Габора , $g (t - u) e^{j ζ t}$ , является стандартным анализом Габора. Варьируя u, вы принимаете только значения f (t) в ближайшее время u. Поддержка $g (t)$ определяет размер окрестности в ближайшее время u. Преобразование Фурье $g_{u, ζ} (t) = g (t - u) e^{ζ t}$ перевод ζ Преобразования Фурье $g (t)$ и дается

${\hat{g}}_{u, ζ} (ω) = e^{- (ω - ζ)} \hat{g} (ω - ζ) .$

Энергетическая концентрация ${\hat{g}}_{u, ζ} (ω)$ имеет отклонение Если окно, $g_{u, ζ} (t) = g (t - u) e^{ζ t}$ , сдвиги на регулярной сетке, преобразование Фурье продукта сдвинутого окна и f (t) является коротковременным преобразованием Фурье (STFT). Плиточное размещение STFT частотно-временной плоскости может быть представлена в виде сетки коробок, каждый с центром (u,

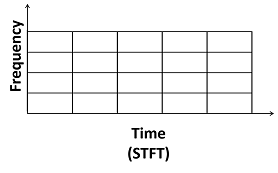
Набор функций ${g_{u, ζ}}$ известен как система координат Габора. Элементы этого множества называются атомами Габора. Система координат является набором функций, {_hk (t)}, которые удовлетворяют следующему условию: существуют константы 0 < A ≤ B < ∞ так что для любой функции f (t),

$A ‖ f ‖^{2} \leq Σ_{k} | 〈 f, h_{k} 〉 |^{2} \leq B ‖ f ‖^{2} .$

Энергетическая концентрация $g (t)$ , во времени, имеет отклонение Энергетическая концентрация $\hat{g} (ω)$ , по частоте, имеет отклонение Концентрация энергии определяет, насколько хорошо окно локализует сигнал во времени и частоте. По принципу частотно-временной неопределенности существует предел того, насколько хорошо вы можете одновременно локализоваться как во временной, так и в частотной областях, на что указывает

$σ_{t} σ_{ω} \geq \frac{1}{2} .$

Сужение окна в одной области приводит к ухудшению локализации в другой области. Габор показал, что площадь окна минимальна, когда $g (t)$ Гауссов.

Преобразование Константа-Q

В CQT ширина полосы пропускания и плотность дискретизации по частоте изменяются. Окна строятся и применяются непосредственно в частотный диапазон. Различные окна имеют различные центральные частоты и полосы пропускания, но отношение центральной частоты к полосе пропускания остается постоянным. Поддержание постоянного соотношения подразумевает:

Разрешение во времени улучшается на более высоких частотах.
Разрешение в частоте улучшается на более низких частотах.

Временные сдвиги для каждого окна зависят от полосы пропускания, из-за принципа неопределенности.

CQT зависит от:

Оконные функции _gk являются реальными, четными функциями. В частотный диапазон преобразование Фурье _gk задано на интервале, [-Fs/2, Fs/2].
Частота дискретизации,
Количество интервалов на октаву, b.
Минимальные и максимальные частоты,

Выберите минимальную частоту _и количество интервалов на октаву b. Затем сформируйте последовательность геометрически разнесенных частот,

_{, k} = _{и мин} × 2^k/b

для k = 0,..., K, где K является целым числом, таким образом,, _что, Шумовая полоса на k-й частоте задана равной Учитывая эту выборку, отношение k-й центральной частоты к ширине полосы пропускания окна не зависит от k:

Q = _ζk/Δk = (2^1/b-2^-1/b)^-1.

Для обеспечения совершенной реконструкции компонент DC и частота Nyquist подготовлены и добавлены, соответственно, к последовательности.

W (в) формирует оконные функции _gk. W (в) является действительной, даже непрерывной функцией, которая центрирована в 0, положительная в интервале [- ½, ½] и 0 в другом месте. W (в) переводится на каждую центральную _{частоту}, а затем масштабируется. Оценка масштабированной и переведенной версии W (в) приводит к _{коэффициентам} фильтра gk [m], заданным как

_gk [m] = W ((m

для m = 0,..., L-1, где L - длина сигнала. По умолчанию ,cqt использует 'hann' окно.

По принципу неопределенности размер полосы пропускания ограничивает значение временных сдвигов. Чтобы удовлетворить неравенству системы координат, shift _akof _gk должен удовлетворять

_ak ≤

Как упоминалось выше, окно применяется в частотный диапазон. Фильтры _gk, центрированные на, формируются и применяются к преобразованию Фурье сигнала. Взятие обратного преобразования получает коэффициенты константы Q.

Ссылки

[1] Holighaus, N., M. Dörfler, G.A. Velasco, and T. Grill. «среда для инвертируемых преобразований Q в реальном времени». Транзакции IEEE по обработке звука, речи и языка. Том 21, № 4, 2013, с. 775-785.

[2] Веласко, Г. А., Н. Холигхаус, М. Дёрфлер и Т. Гриль. «Построение инвертируемого преобразования константы Q с нестационарными системами координат Габора». В работе 14-й Международной конференции по цифровому аудио Эффектов (DAFx-11). Париж, Франция: 2011.

[3] Schörkhuber, C., A. Klapuri, N. Holighaus, and M. Dörfler. Matlab Toolbox for Effective Perfect Reconstruction Time-Frequency Transforms with Log-Frequency Resolution (неопр.) (недоступная ссылка). Представлен на 53-й Международной конференции AES по семантическому аудио. Лондон, Великобритания: 2014.

[4] Пруша, З., П. Л. Сёндергаард, Н. Холигхаус, К. Висмейр, и П. Балаж. Large Частотно-временной Анализ Toolbox 2.0. Sound, Music, and Motion, Lecture Notes in Computer Science 2014, стр. 419-442. https://github.com/ltfat

См. также

cqt | icqt

Документация