Мультисигнальное 1-D вейвлет пакета
wpt = dwpt(X)X. Область входа X является действительным вектором, матрицей или расписанием. По умолчанию в fk18 используется вейвлет, и уровень разложения floor(log2(Ns)), где Ns количество выборок данных. Преобразование вейвлет wpt - массив ячеек 1 N байта, где N = 2^floor(log2(Ns)).
[ также возвращает уровни преобразования узлов wpt,l,packetlevels] = dwpt(___)wpt использование любого из предыдущих синтаксисов.
[ также возвращает центральные частоты приблизительных полос пропускания в циклах на выборку с использованием любого из предыдущих синтаксисов.wpt,l,packetlevels,f] = dwpt(___)
[ также возвращает относительную энергию для вейвлета пакетов в wpt,l,packetlevels,f,re] = dwpt(___)wpt использование любого из предыдущих синтаксисов. Относительная энергия является долей энергии, содержащейся в каждом вейвлет, по уровням.
[___] = dwpt(___, задает опции, использующие аргументы пары "имя-значение" в дополнение к входным параметрам в предыдущих синтаксисах. Для примера, Name,Value)'Level',4 задает уровень разложения.
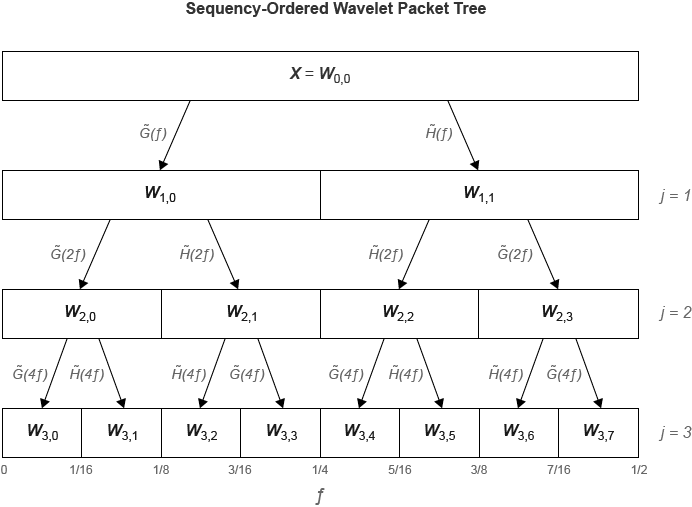
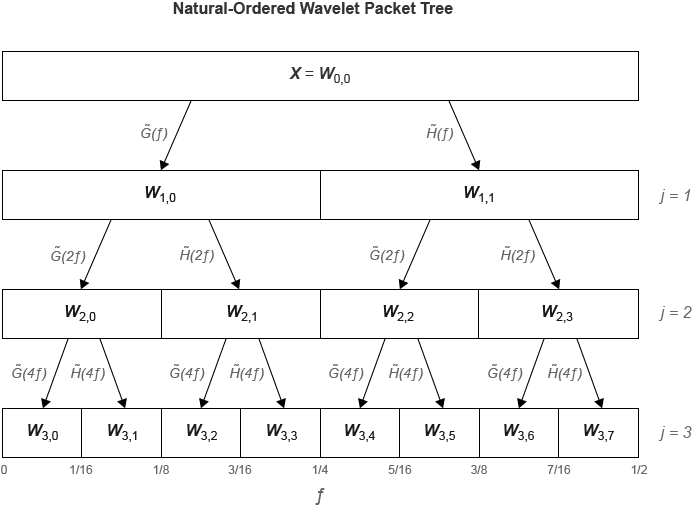
dwpt функция выполняет дискретное преобразование вейвлета пакета и создает упорядоченное по последовательности вейвлетом дерево пакетов. Сравните упорядоченные по последовательности и нормальные (Paley) деревья . - фильтр масштабирования (lowpass) анализа, и представляет фильтр вейвлет (highpass) анализа. На метках внизу показан разбиение частотной оси [0, ½].
[1] Викерхаузер, Младен Виктор. Адаптированный анализ вейвлет от теории к программному обеспечению. Wellesley, MA: A.K. Peters, 1994.
[2] Персиваль, Д. Б., и А. Т. Уолден. Вейвлет для анализа временных рядов. Кембридж, Великобритания: Cambridge University Press, 2000.
[3] Меса, Гектор. «Адаптированные вейвлеты для обнаружения шаблона». В Прогресс Pattern Recognition, Image Analysis and Applications, под редакцией Альберто Санфелиу и Мануэля Лазо Кортеса, 3773: 933-44. Берлин, Гейдельберг: Спрингер Берлин Гейдельберг, 2005. https://doi.org/10.1007/11578079_96 .