Одноуровневое 1-D дискретное вейвлет
[ возвращает одноуровневое дискретное вейвлет (DWT) вектора cA,cD] = dwt(x,wname)x использование вейвлета, заданного как wname. Вейвлет должен быть распознан wavemngr. dwt возвращает вектор коэффициентов приближения cA и вектор коэффициентов детализации cD DWT.
Примечание
Если ваше приложение требует многоуровневого вейвлет, рассмотрите использование wavedec.
[ возвращает одноуровневый DWT с заданным режимом расширения cA,cD] = dwt(___,'mode',extmode)extmode. Для получения дополнительной информации см. dwtmode. Этот аргумент может быть добавлен к любому из предыдущих входных синтаксисов.
Примечание
Для gpuArray входы, поддерживаемые режимы 'symh' ('sym') и 'per'. Все 'mode' опции, кроме 'per' преобразуются в 'symh'. См. пример Одноуровневое дискретное вейвлет на графическом процессоре.
Начиная с s сигналов длины N, вычисляются два набора коэффициентов: коэффициенты аппроксимации cA 1 и коэффициенты детализации cD 1. Свертка s с помощью масштабирующего фильтра LoD, с последующего диадического десятикратного уменьшения, приводит к получению коэффициентов приближения. Точно так же свертка s с вейвлет HiD, с последующим диадическим десятикратным уменьшением, приводит к коэффициентам детализации.
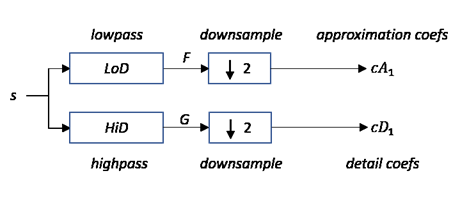
где
![]() - Свертка с фильтром X
- Свертка с фильтром X
- Downsample (сохранить четные индексированные элементы)
Длина каждого фильтра равна 2 n. Если N = длина (<reservedrangesplaceholder6>), сигналы <reservedrangesplaceholder5> и <reservedrangesplaceholder4> имеют длину N +, 2 <reservedrangesplaceholder2> −1 и коэффициенты <reservedrangesplaceholder1> 1 и <reservedrangesplaceholder0> 1 имеют пол длины.
Чтобы справиться с эффектами конца сигнала, возникающими из основанного на свертке алгоритма, глобальной переменной, управляемой dwtmode определяет тип используемого режима расширения сигнала. Возможные опции включают заполнение нулями и симметричное расширение, которое является режимом по умолчанию.
Примечание
Для того же входа, dwt функция и блок DWT в DSP System Toolbox™ не дают одинаковых результатов. Блок DWT предназначен для реализации в реальном времени, в то время как программное обеспечение Wavelet Toolbox™ предназначено для анализа, поэтому продукты обрабатывают граничные условия и состояния фильтра по-разному.
Чтобы сделать dwt выход функции соответствует выходу DWT, установите условие контура функции в нули заполнения путем ввода dwtmode('zpd') в MATLAB® командная строка. Чтобы соответствовать задержке блока DWT, которая реализована с помощью конечной импульсной характеристики фильтров, добавьте нули к входу dwt функция. Количество добавленных нулей должно быть меньше половины длины фильтра.
[1] Daubechies, I. Ten Lectures on Wavelets. Серия региональных конференций CBMS-NSF по прикладной математике. Филадельфия, Пенсильвания: Общество промышленной и прикладной математики, 1992.
[2] Mallat, S. G. «A Theory for Multirresolution Signal Decomposition: The Wavelet Representation». Транзакции IEEE по шаблонному анализу и машинному анализу. Том 11, выпуск 7, июль 1989 года, стр. 674-693.
[3] Meyer, Y. Wavelets and Operators. Перевод Д. Х. Сэлинджера. Кембридж, Великобритания: Cambridge University Press, 1995.
dwtfilterbank | dwtmode | idwt | wavedec | waveinfo