Exponenta Banner

dwtleader

Оценки многофракционных 1-D вейвлет

Свернуть все на странице

Синтаксис

[dh,h] = dwtleader(x)
[dh,h,cp] = dwtleader(x)
[dh,h,cp,tauq] = dwtleader(x)
[dh,h,cp,tauq,leaders] = dwtleader(___)
[dh,h,cp,tauq,leaders,structfunc] = dwtleader(___)
[___]= dwtleader(x,wname)
[___] = dwtleader(___,Name,Value)

Описание

пример

[dh,h] = dwtleader(x) возвращает особенность спектр, dh, и Держатель выражает, h, для 1-D реальных данных, x. Спектр сингулярности и экспоненты Держателя оцениваются для линейно разнесенных моментов функции структуры от -5 до + 5.

пример

[dh,h,cp] = dwtleader(x) также возвращает первые три логарифмических кумулянта, cp масштабирующих экспонент.

пример

[dh,h,cp,tauq] = dwtleader(x) также возвращает степени масштабирования для линейно разнесенных моментов от -5 до 5. Вейвлет не определены для самой мелкой шкалы.

[dh,h,cp,tauq,leaders] = dwtleader(___) также возвращает вейвлет выноски по шкале.

[dh,h,cp,tauq,leaders,structfunc] = dwtleader(___) также возвращает мультиразрешение функции структуры.

[___]= dwtleader(x,wname) использует ортогональный или биортогональный вейвлет, заданный как wname вычислить лидеры вейвлет и фрактальные оценки.

[___] = dwtleader(___,Name,Value) возвращает выноски вейвлет и другие заданные выходы с дополнительными опциями, заданными одним или несколькими Name,Value аргументы в виде пар.

Примеры

свернуть все

Открыть Live Script

Сравните мультифрактальный спектр данных о вариабельности сердечного ритма до и после применения препарата, который снижает динамику сердца.

load hrvDrug
predrug = hrvDrug(1:4642);
postdrug = hrvDrug(4643:end);
[dhpre,hpre] = dwtleader(predrug);
[dhpost,hpost] = dwtleader(postdrug);
plot(hpre,dhpre,hpost,dhpost)
xlabel('h')
ylabel('D(h)')
grid on
legend('Predrug','Postdrug')

Figure contains an axes. The axes contains 2 objects of type line. These objects represent Predrug, Postdrug.

Разброс значений экспоненты Держателя перед введением лекарственного средства (приблизительно от 0,08 до 0,55) намного больше, чем разброс значений после (приблизительно от 0,08 до 0,31). Это указывает на то, что частота сердечных сокращений стала более монофрактальной.

Открыть Live Script

Вычислите спектр особенности и кумулянты для процесса броуновского шума.

Создайте сигнал брауновского шума.

rng(100);
x = cumsum(randn(2^15,1));

Получите и постройте график особенности спектра.

[dh,h,cp] = dwtleader(x);
plot(h,dh,'o-','MarkerFaceColor','b') 
grid on
title({'Singularity Spectrum'; ['First Cumulant ' num2str(cp(1))]})

Figure contains an axes. The axes with title Singularity Spectrum First Cumulant 0.45539 contains an object of type line.

Небольшой разброс в экспонентах Держателя (приблизительно от 0,472 до 0,512) указывает, что этот сигнал шума Брауна может быть охарактеризован глобальным экспонентом Держателя 0,49875. Теоретический показатель Держателя для броуновского движения равен 0,5.

Получите кумуляты.

cp
cp = 1×3

    0.4554   -0.0121   -0.0000

Первое совокупное значение является наклоном масштабируемых экспонент от моментов. Второй и третий кумулянты указывают на отклонение от линейности. Первое совокупное значение и почти нулевые значения второй и третьей совокупностей указывают, что масштабные экспоненты являются линейной функцией моментов. Поэтому этот брауновский сигнал движения является монофрактальным.

Открыть Live Script

Вычислите кумулянты для многофракционной случайной прогулки. Мультифрактальная случайная прогулка является реализацией случайного процесса с теоретическим первым кумулянтом 0,75 и вторым кумулянтом -0,05. Второе совокупное значение -0,05 указывает, что степени масштабирования отклоняются от линейной функции с наклоном 0,75.

Загрузите случайный сигнал обхода. 

load mrw07505

Получите и отобразите первую и вторую кумулянты.

[~,~,cp,tauq] = dwtleader(mrw07505);
cp([1 2])
ans = 1×2

    0.7504   -0.0554

Для монофрактальных процессов степени масштабирования являются линейной функцией моментов. Линейность обозначается тем, что вторая и третья совокупности близки к нулю. В этом случае ненулевой второй кумулянт указывает, что процесс является многофракторным.

Постройте график показателей масштабирования для q-го момента.

plot(-5:5,tauq,'bo--')
title('Estimated Scaling Exponents')
grid on
xlabel('qth Moments')
ylabel('\tau(q)')

Figure contains an axes. The axes with title Estimated Scaling Exponents contains an object of type line.

Масштабирующие экспоненты являются нелинейной функцией моментов.

Входные параметры

свернуть все

Входной сигнал, заданный как 1-D вектор вещественных значений. Для вейвлет по умолчанию и минимального уровня регрессии временные ряды должен иметь не менее 248 выборки. Для значений, не имеющих значения по умолчанию, минимальная необходимая длина данных зависит от вейвлет и уровней, используемых в регрессионой модели. Техника вейвлета leaders лучше всего работает для данных с 8000 или более выборок.

Имя вейвлета, заданное как вектор символов или строковый скаляр. wname - краткое имя семейства вейвлетов и номер фильтра, распознаваемые менеджером вейвлетов, wavemngr.

Чтобы запросить допустимые краткие имена семейства вейвлет, используйте wavemngr('read'). Чтобы определить, является ли конкретный вейвлет ортогональным или биортогональным, используйте waveinfo с кратким именем семейства вейвлет, например waveinfo('db'). Кроме того, используйте wavemngr с 'type' опция, для примера, wavemngr('type','fk4'). Возвращенное значение 1 указывает ортогональный вейвлет. Возвращенное значение 2 указывает биортогональный вейвлет.

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

Пример: 'MinRegressionLevel',5 устанавливает минимальный уровень регрессии равный 5.

Опция веса для использования в взвешенной регрессионой модели методом наименьших квадратов для определения спектра особенности, экспонентов Холдера, кумулянтов и масштабирующих экспонентов, заданных как разделенная разделенными запятой парами, состоящая из 'RegressionWeight' и любой из них 'uniform' или 'scale'. The 'uniform' опция применяет одинаковый вес к каждой шкале. The 'scale' Опция использует количество выносок вейвлета по шкале в качестве весов.

Примечание

Чтобы дублировать поведение dwtleader найденные в релизах до R2018a, обновить все образцы dwtleader чтобы включить аргумент пары "имя-значение" 'RegressionWeight' установлено на 'scale'.

Минимальный уровень регрессии, minlev, задается как разделенная разделенными запятой парами, состоящая из 'MinRegressionLevel' и положительное целое число, больше или равное 2. В многофракционных оценках используются только уровни, большие или равные заданному минимальному уровню. dwtleader требует, по крайней мере, 6 вейвлетов лидеров на максимальном уровне и два уровня, которые будут использоваться в многофракционных оценках. Шкала в дискретном вейвлете преобразовании, соответствующем минимальному уровню, равна двумminlev. Чем более сглажены данные (то есть чем ближе экспоненты Holder к 1), тем меньше вероятность того, что уменьшение минимального уровня регрессии ухудшит результаты.

Максимальный уровень регрессии, maxlev, задается как положительное целое число, больше или равное minlev + 1. Максимальный уровень использует только уровни, меньше чем или равные maxlev в многофракционных оценках. Шкала в дискретном вейвлете преобразовании, соответствующем максимальному уровню, равна 2maxlev. Задайте максимальный уровень регрессии, когда вы хотите ограничить уровни, используемые в регрессии, значением, меньшим, чем уровень по умолчанию. Чтобы определить количество вейвлет по уровням, используйте leaders выходной аргумент или weights поле structfunc выходной аргумент. Значение по умолчанию является самым большим уровнем с по крайней мере шестью вейвлет

Выходные аргументы

свернуть все

Спектр особенности, возвращенный как вектор. Спектр особенности оценивается с помощью структурных функций, определенных для линейно-разнесенных моментов от -5 до 5. Функции структуры вычисляются на основе лидеров вейвлетов, полученных с помощью биортогонального сплайна вейвлета фильтра. Используемый биортогональный сплайн вейвлет-фильтр имеет один момент исчезновения в вейвлете синтеза и пять моментов исчезновения в вейвлете анализа ('bior1.5'). По умолчанию многофракционные оценки получаются от лидеров вейвлета на минимальном уровне 3 и максимальном уровне, где существует по крайней мере шесть вейвлеты лидеров.

Оценки Holder exponent, возвращенные как вектор 1 на 11 скаляров. Экспоненты держателя характеризуют регулярность сигнала. Чем ближе экспонента Держателя к 1, тем ближе функция к дифференцируемой. И наоборот, чем ближе показатель Держателя к нулю, тем ближе функция к прерывистому.

Типы данных: double

Кумулянты, возвращенные как вектор 1 на 3 скаляров. Вектор содержит первые три логарифмических совокупности показателей масштабирования. Первый кумулянт характеризует линейное поведение в масштабирующих показателях. Второй и третий кумулянты характеризуют отходы от линейности.

Типы данных: double

Масштабирование экспонентов, возвращается как вектор-столбец. Экспоненты предназначены для линейно-разнесенных моментов от -5 до + 5 .

leaders - массив ячеек с i-м элементом, содержащим лидеры вейвлета на уровне i + 1 или шкала 2(i +1). Вейвлет не заданы на уровне 1.

Мультиразрешения для глобальных оценок Holder exponent, возвращенные как struct. Структурная функция для x данных определяется как

S(q,a)=1na∑k=1na|Tx(a,k)|q≃aζ(q),

где a - шкала, q - момент, Tx - вейвлет лидеры по шкале, na - количество вейвлета лидеров в каждой шкале, и ζ(q) - экспонента масштабирования. Расширение ζ(q) к полиному производит

ζ(q)=c1q+c2q2/2+c3q3/6+...

Степени масштабирования могут быть оценены из логарифмических совокупностей коэффициентов лидера вейвлета. Когда ζ(q) является линейной функцией, сигнал монофрактальный. Когда он отклоняется от линейного, сигнал является многофракторным.

structfunc - массив структур, содержащий следующие поля:

  • Tq - Измерения входов, x, в различных шкалах. Tq является матрицей мультиразрешений, которые зависят совместно от времени и шкалы. Явления масштабирования в x подразумевают властно-правовую связь между моментами Tq и шкала. Для dwtleader, а Tq поле является Ns -by-36 матрицей, где Ns - количество шкал, используемых в многофракционных оценках. Первые 11 столбцов Tq являются оценками степени масштабирования по шкале для каждого из q-х моментов от -5 до 5. Следующие 11 столбцов содержат оценки спектральной особенности, dh, для каждого из q-х моментов. Столбцы 23-33 содержат оценки Holder exponent, h. Последние три столбца содержат оценки для кумулятов первого, второго и третьего порядков, соответственно.

  • weights - Веса, используемые в регрессии. Веса являются количеством вейвлет по шкалам. weights является вектором Ns -by-1.

  • logscales - Шкалы, используемые в качестве предикторов в регрессии. logscales является вектором Ns -by-1 с логарифмом базы-2 шкал .

Алгоритмы

Вейвлет получают из критически выбранных коэффициентов дискретного вейвлет (DWT). Лидеры вейвлет предлагают значительные теоретические преимущества по сравнению с вейвлет-коэффициентами в многофракторном формализме. Вейвлеты leaders являются временно- или пространственно-локализованной супремой абсолютного значения дискретных коэффициентов вейвлета. Временная локализация супремы требует, чтобы вейвлет-коэффициенты были получены с использованием компактно поддерживаемого вейвлета. Экспоненты Держателя, которые количественно определяют локальную регулярность, определяются из этих супрем. Спектр особенности указывает размер набора экспонентов Holder в данных.

1-D вейвлет определяются как

Lx(j,k)=supλ'⊂3λj,k|dx(j,k)|

где шкалы 2j, переведен во временные положения 2jk. Время соседства 3λj,k=λj,k−1∪λj,k∪λj,k+1, где λj,k=[k2j,(k+1)2j). Время соседства принимается по шкале и все более мелкие шкалы. dx(j,k) являются коэффициентами вейвлета.

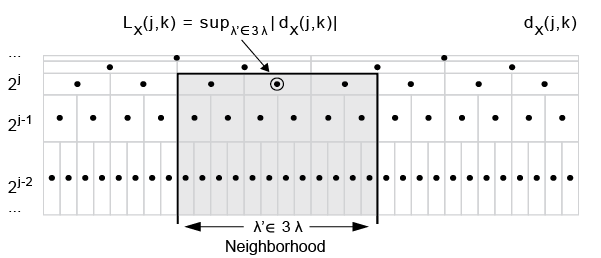
Чтобы вычислить вейвлет, Lx(j,k):

  1. Вычислите коэффициенты вейвлета, dx(j,k), с помощью дискретного преобразования вейвлета и сохраните абсолютное значение каждого коэффициента для каждой шкалы. Каждая более мелкая шкала имеет в два раза больше коэффициентов, чем следующая более грубая шкала. Каждый диадический интервал в шкале 2j может быть записано как объединение двух интервалов в более мелкой шкале.

    [2jk,2j(k+1))=[2j−1(2k),2j−1(2k+2))[2j−1(2k),2j−1(2k+2))=[2j−1(2k),2j−1(2k+1))∪[2j−1(2k+1),2j−1(2k+2))

  2. Начните со шкалы, которая на один уровень грубее, чем самая мелкая полученная шкала.

  3. Сравните первое значение со всеми более мелкими диадическими интервалами и получите максимальное значение.

  4. Перейдите к следующему значению и сравните его значение со всеми более мелкими значениями шкалы.

  5. Продолжите сравнение значений с их вложенными значениями и получение максимумов.

  6. Из максимальных значений, полученных для этой шкалы, исследуйте первые три значения и получите максимальное число этих соседей. Это максимальное значение является выноской для этой шкалы.

  7. Продолжите сравнение максимальных значений, чтобы получить другие выноски для этой шкалы.

  8. Перейдите к следующей более грубой шкале и повторите процесс.

Например, предположим, что у вас есть эти абсолютные значения коэффициентов в этих шкалах:

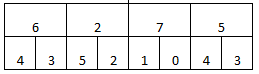
Начиная с верхней строки, которая является следующим самым грубым уровнем из самой мелкой шкалы (нижняя строка), сравните каждое значение с его диадическими интервалами и получите максимумы.

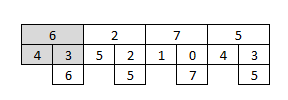
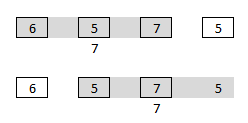
Затем посмотрите на три соседних значения и получите максимальное. Повторите для следующих трех соседей. Эти максимумы 7 и 7 являются вейвлетом лидерами на этом уровне.

Ссылки

[1] Вендт, Х. и П. Эбри. «Многофракциональные тесты с использованием Bootstrapped Wavelet Leaders». Транзакции IEEE по обработке сигналов. Том 55, № 10, 2007, стр. 4811-4820.

[2] Jaffard, S., B. Lashermes, and P. Abry. Wavelet Leaders in Multifractal Analysis (неопр.) (недоступная ссылка). Вейвлет и приложения. Т. Цянь, М. И. Ваи, и X. Юэшэн, эдс. 2006, стр 219–264.

См. также

|

Темы

Введенный в R2016b

Документация по Wavelet Toolbox

Поддержка