Шумоподавление вейвлетов
[X_DEN,NPC,NESTCOV,DEC_DEN,PCA_Params,DEN_Params]
= ...
wmulden(X,LEVEL,WNAME,NPC_APP,NPC_FIN,TPTR,SORH)
[...] = wmulden(X,LEVEL,WNAME,'mode',EXTMODE,NPC_APP,...)
[...] = wmulden(DEC,NPC_APP)
[...] = wmulden(X,LEVEL,WNAME,'mode',EXTMODE,NPC_APP)
[DEC,PCA_Params] = wmulden('estimate',DEC,NPC_APP,NPC_FIN)
[X_DEN,NPC,DEC_DEN,PCA_Params] = wmulden('execute',DEC,PC_Params)
[X_DEN,NPC,NESTCOV,DEC_DEN,PCA_Params,DEN_Params]
= ... или
wmulden(X,LEVEL,WNAME,NPC_APP,NPC_FIN,TPTR,SORH)
[...] = wmulden(X,LEVEL,WNAME,'mode',EXTMODE,NPC_APP,...) возвращает деноизированную версию X_DEN матрицы входа X. Стратегия комбинирует одномерное шумоподавление вейвлет в базисе, где предполагаемая шумовая ковариационная матрица диагональна с неконцентрированным анализом основных компонентов (PCA) на приближениях в области вейвлет или с конечным PCA.
Матрица входа X содержит P сигналы длины N сохраняются столбцово где N > P.
Вейвлет выполняется с использованием уровня разложения LEVEL и вейвлет WNAME.
EXTMODE - расширенный режим для DWT (См. dwtmode).
Если разложение DEC полученный с использованием mdwtdec доступно, вы можете использовать
[...] = wmulden(DEC,NPC_APP) вместо
[...] = wmulden(X,LEVEL,WNAME,'mode',EXTMODE,NPC_APP).
Методы выбора входа NPC_APP и NPC_FIN определить способ выбора главных компонентов для приближений на уровне LEVEL в вейвлет области и для окончательного PCA после реконструкции вейвлета, соответственно.
Если NPC_APP (или NPC_FIN) - целое число, оно содержит количество сохраненных главных компонентов для приближений на уровне LEVEL (или для окончательного PCA после вейвлет-реконструкции).
NPC_XXX должна быть такой, чтобы 0 < = NPC_XXX <= P
NPC_APP или NPC_FIN = 'kais' или 'heur' выбирает количество сохраненных основных компонентов, используя правило Кайзера или эвристическое правило автоматически.
Правило Кайзера сохраняет компоненты, сопоставленные с собственными значениями, большими, чем среднее значение всех собственных значений.
Эвристическое правило сохраняет компоненты, сопоставленные с собственными значениями, более чем в 0,05 раза превышающими сумму всех собственных значений.
NPC_APP или NPC_FIN = 'none' эквивалентно NPC_APP или NPC_FIN = P.
Значения по умолчанию для параметров шумоподавления TPTR и SORH:
TPTR = 'sqtwolog' и SORH = 's'
Допустимые значения для TPTR являются
'rigsure', 'heursure', 'sqtwolog', 'minimaxi', 'penalhi', 'penalme', 'penallo'
Допустимые значения для SORH:
's' (soft) or 'h' (hard)
X_DEN является деноизированной версией матрицы входа X.
NPC - вектор выбранных чисел сохраненных главных компонентов.
NESTCOV - оценочная шумовая ковариационная матрица, полученная с использованием оценки минимального ковариационного определяющего (MCD).
DEC_DEN - вейвлет X_DEN.
PCA_Params является такой структурой, что:
PCA_Params.NEST = {pc_NEST,var_NEST,NESTCOV}
PCA_Params.APP = {pc_APP,var_APP,npc_APP}
PCA_Params.FIN = {pc_FIN,var_FIN,npc_FIN}
где:
pc_XXX является P-by- P матрица главных компонентов.
Столбцы хранятся в порядке убывания отклонений.
var_XXX является основным вектором отклонений компонента.
NESTCOV - ковариация матрицы для деталей на уровне 1.
DEN_Params является такой структурой, что:
DEN_Params.thrVAL является вектором длины LEVEL который содержит пороговые значения для каждого уровня.
DEN_Params.thrMETH - вектор символов, содержащий имя метода шумоподавления (TPTR).
DEN_Params.thrTYPE - переменный символ, содержащая тип порогового значения (SORH).
[DEC,PCA_Params] = wmulden('estimate',DEC,NPC_APP,NPC_FIN) возвращает разложение вейвлета DEC и оценки основных компонентов PCA_Params.
[X_DEN,NPC,DEC_DEN,PCA_Params] = wmulden( использует оценки основных компонентов 'execute',DEC,PC_Params)PCA_Params ранее вычисленный.
Значение входа DEC может быть заменено на X, LEVEL, и WNAME.
% Load a multivariate signal x together with
% the original signals (x_orig) and true noise
% covariance matrix (covar).
load ex4mwden
% Set the denoising method parameters.
level = 5;
wname = 'sym4';
tptr = 'sqtwolog';
sorh = 's';
% Set the PCA parameters to select the number of
% retained principal components automatically by
% Kaiser's rule.
npc_app = 'kais';
npc_fin = 'kais';
% Perform multivariate denoising.
[x_den, npc, nestco] = wmulden(x, level, wname, npc_app, ...
npc_fin, tptr, sorh);
% Display the original and denoised signals.
kp = 0;
for i = 1:4
subplot(4,3,kp+1), plot(x_orig(:,i));
title(['Original signal ',num2str(i)])
subplot(4,3,kp+2), plot(x(:,i));
title(['Observed signal ',num2str(i)])
subplot(4,3,kp+3), plot(x_den(:,i));
title(['Denoised signal ',num2str(i)])
kp = kp + 3;
end
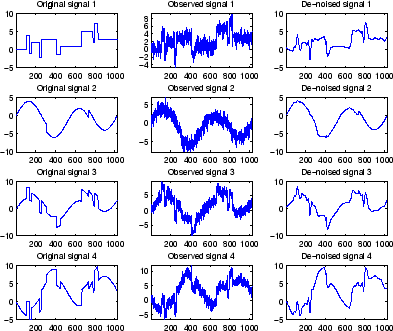
% The results are good: the first function, which is
% irregular, is correctly recovered while the second
% function, more regular, is well denoised.
% The second output argument gives the numbers
% of retained principal components for PCA for
% approximations and for final PCA.
npc
npc =
2 2
% The third output argument contains the estimated
% noise covariance matrix using the MCD based
% on the matrix of finest details.
nestco
nestco =
1.0784 0.8333 0.6878 0.8141
0.8333 1.0025 0.5275 0.6814
0.6878 0.5275 1.0501 0.7734
0.8141 0.6814 0.7734 1.0967
% The estimation is satisfactory since the values are close
% to the true values given by covar.
covar
covar =
1.0000 0.8000 0.6000 0.7000
0.8000 1.0000 0.5000 0.6000
0.6000 0.5000 1.0000 0.7000
0.7000 0.6000 0.7000 1.0000
Многомерная процедура шумоподавления является обобщением одномерной стратегии. Он комбинирует одномерное шумоподавление вейвлет в базисе, где предполагаемая шумовая ковариационная матрица является диагональной и нецентрированным анализом основных компонентов (PCA) на приближениях в области вейвлет или с конечным PCA.
Устойчивая оценка шумовой ковариационной матрицы, заданная минимальным оценщиком ковариационного определяющего, основанная на матрице мельчайших деталей.
Амингхафари, М.; Cheze, N.; Погги, Дж-М. (2006), «Многомерное шумоподавление с использованием вейвлетов и анализа основных компонентов», Computational Statistics & Data Analysis, 50, pp. 2381-2398.
Руссью, П.; Ван Дриссен, К. (1999), «Быстрый алгоритм для оценки минимального ковариационного определяющего», Technometrics, 41, pp. 212-223.