Мы знаем, что классический DWT страдает недостатком: DWT не является инвариантным по времени преобразованием. Это означает, что даже при периодическом расширении сигнала DWT переведенной версии сигнала X в целом не является переведенной версией DWT X.
Как восстановить инвариацию перевода, которая является желаемым свойством, потерянным классическим DWT? Идея состоит в том, чтобы усреднить некоторое немного различное DWT, называемое и децимированное DWT, чтобы задать стационарное вейвлет (SWT). Это свойство полезно для нескольких приложений, таких как обнаружение точек разбиения.
Основное применение SWT - шумоподавление. Для получения дополнительной информации о обосновании см. раздел [CoiD95] в ссылках». Для примеров смотрите 1-D Stationary Wavelet Transform и 2-D Stationary Wavelet Transform.
Принцип состоит в том, чтобы усреднить несколько деноизированных сигналов. Каждый из них получен с помощью обычной схемы шумоподавления (см. "Деноизоляция вейвлет" и непараметрическая оценка функции "), но применен к коэффициентам, DWT с децимированным
Примечание
SWT задается только для сигналов длины, делимой на 2J, где J - максимальный уровень разложения. SWT использует периодический (per) расширение.
Что представляет собой DWT, децимируемый
Существует много немного разных способов обработки дискретного вейвлет. Напомним, что основной вычислительный шаг DWT является сверткой с последующим десятикратным уменьшением. Десятикратное уменьшение сохраняет даже индексированные элементы.
Но десятикратное уменьшение можно было провести, выбрав нечетные индексированные элементы вместо четных индексируемых элементов. Этот выбор касается каждого шага процесса разложения, поэтому на каждом уровне мы выбирали нечетный или четный.
Если мы выполним все различные возможные декомпозиции исходного сигнала, у нас будет 2J различные разложения для заданных J максимального уровня.
Допустим, что на шаге j 1 = 0 или элементы выбор нечетного или даже индексированного j. Каждое разложение маркировано последовательностью 0s и 1 с: ε = ε1..., ε <reservedrangesplaceholder0>. Это преобразование названо
Можно получить базисные векторы и децимированные DWT из векторов стандартных DWT путем применения сдвига и соответствует специальному выбору источника базисных функций.
Для заданного сигнала длины N можно вычислить все DWT с прореживанием, путем вычисления коэффициентов приближения и детализации для каждой возможной последовательности. Выполните это итерационно, слегка измененную версию базового шага DWT формы:
[A,D] = dwt(X,wname,'mode','per','shift',e);
Последние два аргумента определяют способ выполнения шага десятикратного уменьшения. Это классический для e = 0, но для e = 1 нечетные индексированные элементы сохраняются десятикратным уменьшением.
Конечно, это нехороший способ вычислить все и DWT, децимированные, потому что многие расчеты выполняются много раз. Теперь опишем другой способ - стационарное вейвлет (SWT).
Алгоритм SWT очень прост и близок к алгоритму DWT. Точнее, для уровня 1, все и DWT, децимированные, (только два на этом уровне) для данного сигнала могут быть получены путем свертки сигнала с соответствующими фильтрами, как в случае DWT, но без понижающей дискретизации. Тогда приближения и детализации на уровне 1 являются обоими размером N, который является длиной сигнала. Это может быть визуализировано на следующем рисунке.
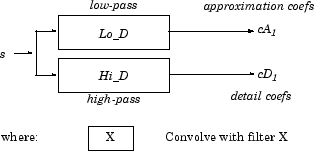
Общий шаг j свертывает коэффициенты приближения на уровне j-1 с увеличенными версиями соответствующих исходных фильтров, чтобы получить коэффициенты приближения и детализации на уровне j. Это может быть визуализировано на следующем рисунке.
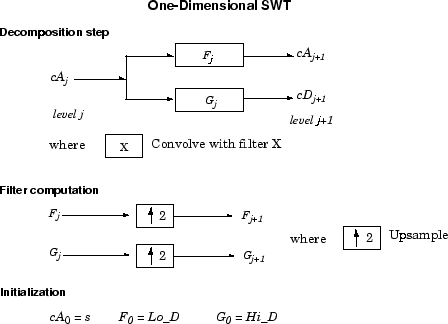
Далее мы проиллюстрироваем, как извлечь заданный, в и дестимулированный DWT из структуры коэффициентов приближения и детализации SWT.
Мы разлагаем последовательность чисел высоты с помощью SWT, на уровне J = 3, используя ортогональный вейвлет.
Функция swt вычисляет последовательно следующие массивы, где A(j,ε1,...,εj) или D(j,ε1,...,εj) обозначают приближение или коэффициент детали на уровне <reservedrangesplaceholder1>, полученном для ε-decimated DWT охарактеризованный ε = [ε1..., ε <reservedrangesplaceholder0>].
A (0) | A (0) | A (0) | A (0) | A (0) | A (0) | A (0) | A (0) |
D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) |
A (1,0) | A (1,1) | A (1,0) | A (1,1) | A (1,0) | A (1,1) | A (1,0) | A (1,1) |
D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) |
D (2,0,0) | D (2,1,0) | D (2,0,1) | D (2,1,1) | D (2,0,0) | D (2,1,0) | D (2,0,1) | D (2,1,1) |
A (2,0,0) | A (2,1,0) | А (2,0,1) | A (2,1,1) | A (2,0,0) | A (2,1,0) | А (2,0,1) | A (2,1,1) |
D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) |
D (2,0,0) | D (2,1,0) | D (2,0,1) | D (2,1,1) | D (2,0,0) | D (2,1,0) | D (2,0,1) | D (2,1,1) |
D (3,0,0,0) | D (3,1,0,0) | D (3,0,1,0) | D (3,1,1,0) | D (3,0,0,1) | D (3,1,0,1) | D (3,0,1,1) | D (3,1,1,1) |
А (3,0,0,0) | А (3,1,0,0) | А (3,0,1,0) | А (3,1,1,0) | А (3,0,0,1) | А (3,1,0,1) | А (3,0,1,1) | А (3,1,1,1) |
Позвольте j обозначить текущий уровень, где j также является текущим шагом алгоритма. Тогда у нас будут следующие абстрактные отношения с и = 0 или 1:
[tmpAPP,tmpDET] = dwt(A(j,ε1, ,ɛj),wname,'mode','per','shift',ɛj+1); A(j+1,ɛ1, ,ɛj,ɛj+1) = circshift(tmpAPP,-ɛj+1); D(j+1,ɛ1, ,ɛj,ɛj+1) = circshift(tmpDET,-ɛj+1);
где circshift выполняет, в, круговое сдвиг входного вектора. Поэтому, если и j + 1 = 0, circshift инструкция неэффективна и может быть подавлена.
Позвольте ε = [ε1..., ε <reservedrangesplaceholder0>] с εi = 0 или 1. У нас есть 2J = 23 = восемь DWT с различными и децимированными, на уровне 3. Выбрав, мы можем извлечь соответствующий и декиматированный DWT из массива SWT.
Теперь рассмотрим последний шаг, J = 3, и предположим, что [C Затем его можно извлечь из структуры разложения SWT путем выбора соответствующих коэффициентов следующим образом:
C, =
А (3, и 1, и 2, и 3) | Д (3, | D (2, и 1, и 2) | D (2, и 1, и 2) | D (1, | D (1, | D (1, | D (1, |
L, = [1,1,2,4,8]
Например, ε-decimated DWT соответствующий ε = [ε1, ε2, ε3] = [1,0,1] показывают в смелом в последовательности массивов предыдущего примера.
Это может быть распространено на 2-D случай. Алгоритм стационарного вейвлет для изображений визуализирован на следующем рисунке.
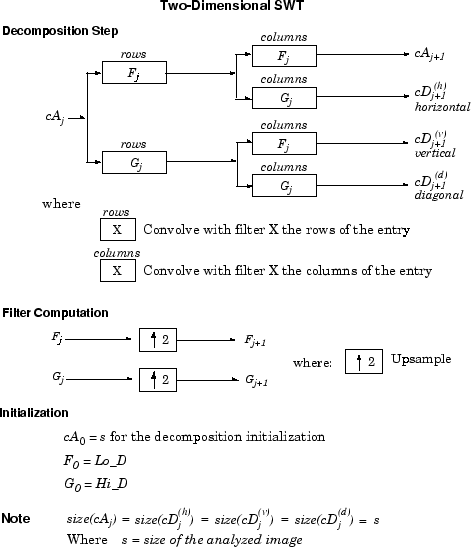
Каждый и DWT, относящийся к заданному, может быть инвертирован.
Чтобы восстановить исходный сигнал с помощью заданного и децимированного DWT, характеризующегося [
FOR j = J:-1:1 A(j-1, ε1, ,ɛj-1) = ... idwt(A(j,ɛ1, ,ɛj),D(S,ɛ1, ,ɛj)],wname,'mode','per','shift',ɛj); END
Для каждого выбора ε = (ε1..., εJ), мы получаем оригинальный сигнал A (0), начинающийся с немного отличающихся разложений и захватывающий по-разному главные функции проанализированного сигнала.
Идея обратного дискретного стационарного вейвлета преобразования состоит в том, чтобы усреднить обратные значения, полученные для каждого и децимированного DWT. Это может быть сделано рекурсивно, начиная с уровня J вниз до уровня 1.
ISWT получается со следующим абстрактным алгоритмом:
FOR j = J:-1:1
X0 = idwt(A(j,ɛ1, ,ɛj),D(j,ɛ1, ,ɛj)],wname, ...
'mode','per','shift',0);
X1 = idwt(A(j,ɛ1, ,ɛj),D(j,ɛ1, ,ɛj)],wname, ...
'mode','per','shift',1);
X1 = circshift(X1,-1);
A(j-1, ɛ1, ,ɛj-1) = (X0+X1)/2;
END
По тем же линиям это может быть распространено и на 2-D корпус.
Некоторые полезные ссылки для стационарного преобразования вейвлет (SWT): [CoiD95], [NasS95] и [PesKC96] в ссылках.