swt
Дискретное стационарное вейвлет 1-D
Описание
Примеры
Многоуровневое стационарное разложение вейвлет
Выполните многоуровневое стационарное вейвлет сигнала.
Загрузите одномерный сигнал и получите его длину.
load noisbloc
s = noisbloc;
sLen = length(s);Выполните стационарное разложение вейвлета на уровне 3 сигнала с помощью 'db1'. Извлеките коэффициенты детализации и приближения на уровне 3.
[swa,swd] = swt(s,3,'db1');
swd3 = swd(3,:);
swa3 = swa(3,:);Постройте график выхода разложения.
plot(s)
xlim([0 sLen])
title('Original Signal')
Постройте график приближения уровня 3 и коэффициентов детализации.
subplot(2,1,1) plot(swa3) xlim([0 sLen]) title('Level 3 Approximation coefficients') subplot(2,1,2) plot(swd3) xlim([0 sLen]) title('Level 3 Detail coefficients')
Входные параметры
Выходные аргументы
Алгоритмы
Учитывая s сигнала длины N, первый шаг стационарного вейвлет (SWT) производит, начиная с s, два набора коэффициентов: коэффициенты приближения cA1 и коэффициенты детализации cD1. Эти векторы получаются сверткой s с lowpass LoD для приближения и с высокочастотным фильтром HiD для детализации.
Точнее, первый шаг -
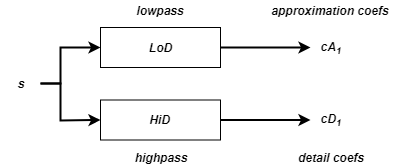
где
обозначает свертку с X фильтра.
Примечание
cA1 и cD1 имеют длину N вместо N/2 как в случае DWT.
Следующий шаг разделяет коэффициенты приближения, cA1 в двух частях, используя ту же схему, но с измененными фильтрами, полученными путем увеличения дискретизации фильтров, используемых для предыдущего шага, и замены s на cA1. Затем SWT производит cA2 и cD2. В более общем плане,
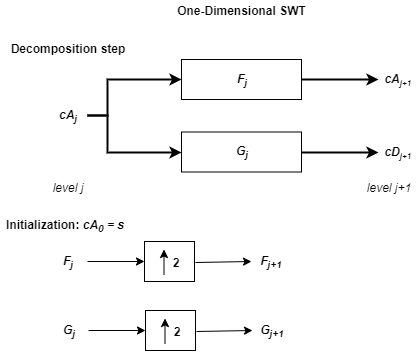
где
<reservedrangesplaceholder1> 0 = LoD
<reservedrangesplaceholder1> 0 = HiD
- Upsample (вставить нули между элементами)
Ссылки
[1] Nason, G. P., and B. W. Silverman. «Стационарное преобразование вейвлет и некоторые статистические приложения». В Вейвлетах и статистике под редакцией Анестиса Антониадиса и Жоржа Oppenheim, 103: 281-99. Нью-Йорк, Нью-Йорк: Спрингер Нью-Йорк, 1995. https://doi.org/10.1007/978-1-4612-2544-7_17.
[2] Койфман, Р. Р. и Д. Л. Донохо. «Переводно-инвариантное шумоподавление». В Вейвлетах и статистике под редакцией Анестиса Антониадиса и Жоржа Oppenheim, 103: 125-50. Нью-Йорк, Нью-Йорк: Спрингер Нью-Йорк, 1995. https://doi.org/10.1007/978-1-4612-2544-7_9.
[3] Pesquet, J.-C., H. Krim, and H. Carfantan. «Инвариантные по времени ортонормальные представления вейвлет». Транзакции IEEE по обработке сигналов 44, № 8 (август 1996 года): 1964-70. https://doi.org/10.1109/78.533717.