Время нарастания, время урегулирования и другие характеристики переходного процесса
stepinfo позволяет вам вычислить характеристики переходного процесса для модели динамической системы или для массива данных переходного процесса. Для переходного процесса y (t), stepinfo вычисляет характеристики относительно yinit и yfinal, где yinit является начальным смещением, то есть, значение, прежде чем шаг будет применен, и yfinal является установившимся значением ответа. Эти значения зависят от синтаксиса, который вы используете.
Для модели sys динамической системы, stepinfo использование yinit = 0 и yfinal = установившееся значение.
Для массива данных переходного процесса [y,t], stepinfo использование yinit = 0 и yfinal = длится демонстрационное значение y, если вы явным образом не задаете эти значения.
Для получения дополнительной информации о как stepinfo вычисляет характеристики переходного процесса, см. Алгоритмы.
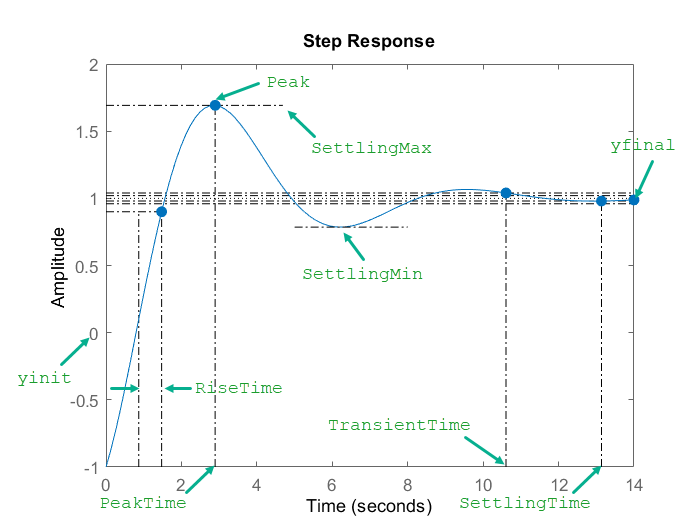
Следующая фигура иллюстрирует некоторые характеристики stepinfo вычисляет для переходного процесса. Для этого ответа примите что y (t) = 0 для t <0, таким образом, yinit = 0.
S = stepinfo(y,t)y и соответствующий временной вектор t. Для откликов системы SISO, y вектор с тем же количеством записей как t. Для данных об ответе MIMO, y массив, содержащий ответы каждого канала ввода-вывода. Этот синтаксис использует yinit = 0 и последнее значение в y (или последнее значение в соответствующих данных об ответе каждого канала) как yfinal.
S = stepinfo(y,t,yfinal)yfinal. Этот синтаксис полезен, когда вы знаете, что ожидаемый установившийся отклик системы отличается от последнего значения в y по причинам, таким как шум измерения. Этот синтаксис использует yinit = 0.
Для ответов SISO, t и y векторы с той же длиной NS. Для систем с NU входные параметры и NY выходные параметры, можно задать y как NS- NY- NU массив (см. step) и yfinal как NY- NU массив. stepinfo затем возвращает NY- NU массивы структур из характеристик ответа, соответствующих каждой паре ввода-вывода.
S = stepinfo(y,t,yfinal,yinit)yinit. Этот синтаксис полезен когда ваш y данные имеют начальное смещение; то есть, y является ненулевым, прежде чем шаг произойдет.
Для ответов SISO, t и y векторы с той же длиной NS. Для систем с NU входные параметры и NY выходные параметры, можно задать y как NS- NY- NU массив и yinit как NY- NU массив. stepinfo затем возвращает NY- NU массивы структур из характеристик ответа, соответствующих каждой паре ввода-вывода.
S = stepinfo(___,'RiseTimeLimits',RT)RT = [0.1 0.9]). Верхний порог RT(2) также используется, чтобы вычислить SettlingMin и SettlingMax. Эти значения являются минимальными и максимальными значениями ответа, происходящего после того, как ответ достигнет верхнего порога. Можно использовать этот синтаксис с любой из предыдущих комбинаций входных аргументов.
Для переходного процесса y (t), stepinfo вычисляет характеристики относительно yinit и yfinal. Для модели sys динамической системы, stepinfo использование yinit = 0 и yfinal = установившееся значение.
Эта таблица показывает как stepinfo вычисляет каждую характеристику.
| Характеристика переходного процесса | Описание |
|---|---|
RiseTime | Время это берет для ответа, чтобы повыситься с 10% до 90% пути от yinit до yfinal |
TransientTime | В первый раз T, таким образом, что ошибка |y (t) – yfinal | ≤ SettlingTimeThreshold × emax для t ≥ T, где emax, является максимальной погрешностью |y (t) – yfinal | для t ≥ 0. По умолчанию, SettlingTimeThreshold = 0.02 (2% пиковой ошибки). Переходное время измеряется, как быстро переходные движущие силы вымирают. |
SettlingTime | В первый раз T, таким образом, что ошибка |y (t) – yfinal | ≤ SettlingTimeThreshold × |yfinal – yinit | для t ≥ T. По умолчанию, |
SettlingMin | Минимальное значение y (t) однажды ответ повысилось |
SettlingMax | Максимальное значение y (t) однажды ответ повысилось |
Overshoot | Перерегулирование процента. Относительно нормированного ответа ynorm (t) = (y (t) – yinit) / (yfinal – yinit), перерегулирование является большим из нуля и 100 × макс. (ynorm (t) – 1). |
Undershoot | Отклонение от номинала процента. Относительно нормированного ответа ynorm (t) отклонение от номинала является меньшим из нуля и –100 × макс. (ynorm (t) – 1). |
Peak | Пиковое значение |y (t) – yinit | |
PeakTime | Время, в которое происходит пиковое значение |