Если библиотека тулбокса не содержит желаемое параметрическое уравнение, можно создать собственное уравнение. Модели библиотеки, однако, предлагают лучшую возможность для быстрой сходимости. Это вызвано тем, что:
Для большинства моделей библиотеки тулбокс вычисляет оптимальные содействующие начальные точки по умолчанию. Для пользовательских моделей тулбокс выбирает случайные начальные точки по умолчанию на интервале [0,1]. Необходимо найти подходящие стартовые точки для пользовательских моделей.
Модели библиотеки используют аналитический якобиан. Пользовательские модели используют конечное дифференцирование.
Можно создать пользовательские общие уравнения с Пользовательским типом подгонки уравнения. Общие модели являются нелинейными комбинациями (возможно, нелинейный) термины. Они заданы уравнениями, которые могут быть нелинейными в параметрах. Пользовательская подгонка уравнения использует нелинейный метод наименьших квадратов подходящая процедура.
Можно определить пользовательское линейное уравнение с помощью Пользовательского типа подгонки уравнения, хотя нелинейный подбор кривой менее эффективен и обычно медленнее, чем подбор кривой линейного метода наименьших квадратов.
Если вы не знаете, может ли ваше уравнение быть описано в виде набора линейных функций, то выберите Custom Equation. Вы можете должны быть искать подходящие стартовые точки.
Если вам нужен линейный метод наименьших квадратов, соответствующий пользовательским уравнениям, выберите Linear Fitting тип модели вместо этого. Смотрите Пользовательский Линейный Подбор кривой.
В приложении Curve Fitting выберите Custom Equation из списка типов модели.
Используйте пользовательскую подгонку уравнения, чтобы определить ваши собственные уравнения. Пользовательское уравнение примера появляется, когда вы выбираете Custom Equation из списка, как показано здесь для данных о кривой.
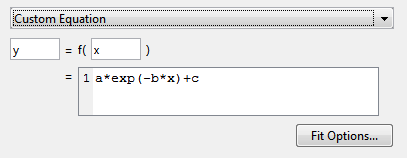
Если у вас есть поверхностные данные, пример, пользовательское уравнение использует и x и y.
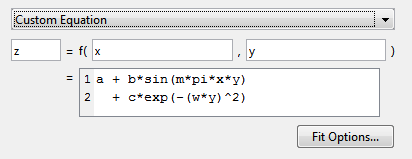
Можно отредактировать xY, и z к любым допустимым именам переменной.
В более низком поле отредактируйте пример, чтобы определить ваше собственное уравнение. Можно ввести любой допустимый MATLAB® выражение в терминах ваших имен переменных. Можно задать функцию или имя скрипта (см. Подбор кривой Кривой, Заданной Файлом в Приложении Curve Fitting).
Нажмите Fit Options, если вы хотите задать стартовые точки или границы. По умолчанию начальные значения являются случайным образом выбранным On интервала [0,1] и неограничены. Вы можете должны быть искать подходящие стартовые точки и границы. Для примера смотрите Пользовательский Нелинейный Анализ данных ENSO.
Если вы устанавливаете подходящие опции и затем изменяете другие подходящие настройки, приложение помнит ваш выбор за нижние и верхние границы и стартовые точки, если это возможно. Поскольку пользовательское приложение уравнений Curve Fitting всегда помнит пользовательские значения, но для многих моделей библиотеки, если вы изменяете подходящие настройки затем, приложение автоматически вычисляет новые оптимальные значения для стартовых точек или нижних границ.
Можно сохранить пользовательские уравнения как часть сохраненной кривой Подходящие сеансы приложения.
Ваша функция может выполниться неоднократно, и во время подбора кривой и во время предварительной обработки перед подбором кривой. Следует иметь в виду, что это может быть длительно, если вы используете функции с побочными эффектами, такими как записывание данные к файлу или отображение диагностической информации к Командному окну.
Для примеров см.:
В этом примере показано, как обеспечить функцию, или скрипт называют как подходящую модель в приложении Curve Fitting. Задайте функцию в файле и используйте его, чтобы соответствовать кривой.
Задайте функцию в файле MATLAB.
function y = piecewiseLine(x,a,b,c,d,k) % PIECEWISELINE A line made of two pieces % that is not continuous. y = zeros(size(x)); % This example includes a for-loop and if statement % purely for example purposes. for i = 1:length(x) if x(i) < k, y(i) = a + b.* x(i); else y(i) = c + d.* x(i); end end end
Сохраните файл на пути MATLAB.
Задайте некоторые данные и откройте приложение Curve Fitting.
x = [0.81;0.91;0.13;0.91;0.63;0.098;0.28;0.55;... 0.96;0.96;0.16;0.97;0.96]; y = [0.17;0.12;0.16;0.0035;0.37;0.082;0.34;0.56;... 0.15;-0.046;0.17;-0.091;-0.071]; cftool
В приложении Curve Fitting выберите x и y в X data и списках Y data.
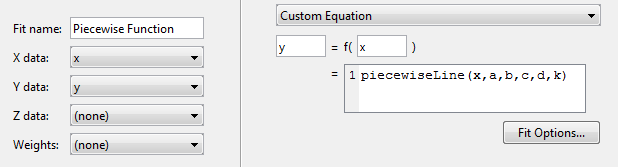
Используйте свой piecewiseLine функция в приложении Curve Fitting путем выбора Пользовательского уравнения соответствует типу, и затем ввода выражения function в пользовательское текстовое поле уравнения. Функция берет x данные и некоторые параметры для подбора кривой.
piecewiseLine( x, a, b, c, d, k )
Приложение Curve Fitting создает подгонку с помощью функции.
Совет
Если вы хотите использовать ту же функцию для подбора кривой в командной строке, используйте то же выражение в качестве входа к fittype, и затем используйте fittype как вход к fit:
ft = fittype('piecewiseLine( x, a, b, c, d, k )');
f = fit( x, y, ft)fit функция.Подбирать пользовательские модели, также:
Предоставьте пользовательскую модель к fit функция в fitType входной параметр. Можно использовать выражение MATLAB (включая любой .m файл), массив ячеек или массив строк линейных терминов модели или анонимная функция.
Создайте fittype объект с fittype функционируйте, чтобы использовать в качестве входного параметра для fit функция.
Этот пример загружает некоторые данные и использует пользовательское уравнение, задающее модель Weibull как вход к fit функция:
time = [ 0.1; 0.1; 0.3; 0.3; 1.3; 1.7; 2.1; 2.6; 3.9; 3.9; ...
5.1; 5.6; 6.2; 6.4; 7.7; 8.1; 8.2; 8.9; 9.0; 9.5; ...
9.6; 10.2; 10.3; 10.8; 11.2; 11.2; 11.2; 11.7; 12.1; 12.3; ...
12.3; 13.1; 13.2; 13.4; 13.7; 14.0; 14.3; 15.4; 16.1; 16.1; ...
16.4; 16.4; 16.7; 16.7; 17.5; 17.6; 18.1; 18.5; 19.3; 19.7;];
conc = [0.01; 0.08; 0.13; 0.16; 0.55; 0.90; 1.11; 1.62; 1.79; 1.59; ...
1.83; 1.68; 2.09; 2.17; 2.66; 2.08; 2.26; 1.65; 1.70; 2.39; ...
2.08; 2.02; 1.65; 1.96; 1.91; 1.30; 1.62; 1.57; 1.32; 1.56; ...
1.36; 1.05; 1.29; 1.32; 1.20; 1.10; 0.88; 0.63; 0.69; 0.69; ...
0.49; 0.53; 0.42; 0.48; 0.41; 0.27; 0.36; 0.33; 0.17; 0.20;];
f = fit( time, conc, 'c*a*b*x^(b-1)*exp(-a*x^b)', 'StartPoint', [0.01, 2, 5] )
plot( f, time, conc )Задавать пользовательское использование модели fittype, используйте форму:
f = fittype(expr)
fittype объект для выражения MATLAB, содержавшегося в векторе символов, строковом скаляре, массиве ячеек, массиве строк или анонимной функции expr.Смотрите fittype страница с описанием для получения дополнительной информации о:
Задавая зависимые и независимые переменные, проблемные параметры и коэффициенты с помощью fittype.
Определение массива ячеек или массива строк терминов, чтобы использовать линейный алгоритм подбора для пользовательского уравнения. Если expr
Для получения дополнительной информации о линейном подборе кривой смотрите Linear Fitting Выбора в Командной строке.
Примеры линейных и нелинейных пользовательских моделей.
Для постепенного примера смотрите, что Пользовательская Нелинейная перепись Соответствует.