Документация

Смещенные оценки

Если выборки проигнорированы, количество отсчетов, используемое по оценке, меньше NumSamples. Очевидно фактическое используемое количество отсчетов должно быть достаточным, чтобы получить оценки. Кроме того, несмотря на то, что параметры модели Parameters (или среднее значение оценивает Mean) несмещенные оценки наибольшего правдоподобия, остаточная оценка ковариации Covariance смещается. Чтобы преобразовать в несмещенную оценку ковариации, умножьте Covariance

где Count фактическое количество отсчетов, используемое по оценке с Count ≤ NumSamples. Ни одна из функций регрессии не выполняет эту корректировку.

Требования

Функции регрессии, особенно функции оценки, имеют несколько требований. Во-первых, у них должны быть сопоставимые значения для NumSamples, NumSeries, и NumParams. Как правило, многомерные нормальные функции регрессии требуют

и функции регрессии наименьших квадратов требуют

где Count фактическое количество отсчетов, используемое по оценке с

Во-вторых, у них должно быть достаточно ненедостающих значений, чтобы сходиться. В-третьих, у них должна быть невырожденная ковариационная матрица.

Несмотря на то, что некоторые необходимые и достаточные условия могут быть найдены в ссылках, общих условиях для существования и уникальности решений в случае недостающих данных, не существовать. Несходимость обычно происходит из-за плохо обусловленной оценки ковариационной матрицы, которая обсуждена более подробно в Несходимости.

Медленная сходимость

Поскольку сходимость худшего случая алгоритма ECM линейна, возможно выполнить сотни и даже тысячи итераций перед завершением алгоритма. Если вы оцениваете с алгоритмом ECM регулярно с регулярными обновлениями, можно использовать предшествующие оценки в качестве исходных предположений для оценки следующего периода. Этот подход часто ускоряет вещи, поскольку инициализация по умолчанию в функциях регрессии устанавливает начальные параметры b обнулять и начальная ковариация C быть единичной матрицей.

Другие импровизированные подходы возможны несмотря на то, что большинство подходов зависимо проблемой. В частности, для среднего значения и оценки ковариации, функции оценки ecmnmle использует функцию ecmninit получить первоначальную оценку.

Неслучайные остаточные значения

Одновременные оценки для параметров b и ковариации C потребуйте C быть положительно-определенным. Так, общие многомерные нормальные стандартные программы регрессии требуют невырожденных остаточных ошибок. Если вы сталкиваетесь с моделью, которая имеет точные результаты, стандартную программу наименьших квадратов ecmlsrmle все еще работает, несмотря на то, что это предоставляет оценке наименьших квадратов сингулярную остаточную ковариационную матрицу. Другая регрессия функционирует сбой.

Несходимость

Несмотря на то, что функции регрессии устойчивы и работают на большинство “типичных” случаев, они могут не сходиться. Основной тип отказа является плохо обусловленной ковариационной матрицей, где отказы являются или мягкими или трудными. Мягкий отказ блуждает бесконечно к почти сингулярной ковариационной матрице и может быть определен, если алгоритму не удается сходиться приблизительно после 100 итераций. Если MaxIterations увеличен до 500, и режим отображения инициируется (без выходных аргументов), типичный мягкий отказ выглядит так.

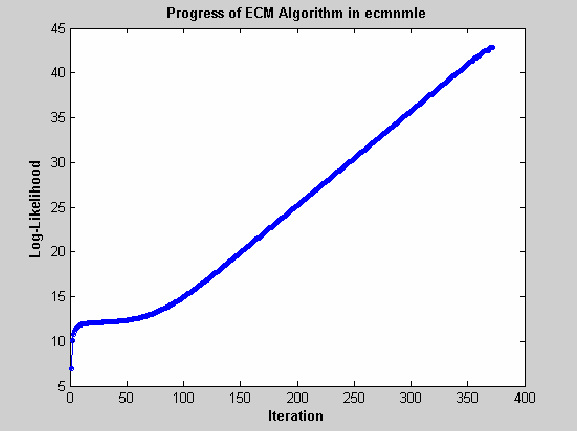
Этот случай, который основан на 20 наблюдениях за пятью активами с 30% пропавших без вести данных, показывает, что логарифмическая правдоподобность переходит линейно к бесконечности, как функция правдоподобия переходит в 0. В этом случае функция сходится, но ковариационная матрица эффективно сингулярна с самым маленьким собственным значением порядка точности машины (eps).

Для функции ecmnmle, серьезная ошибка выглядит так:

> In ecmninit at 60
  In ecmnmle at 140
??? Error using ==> ecmnmle
Full covariance not positive-definite in iteration 218.

С практической точки зрения, если в сомнении, тестируют вашу остаточную ковариационную матрицу от стандартных программ регрессии, чтобы гарантировать, что это положительно-определенно. Это важно, потому что исправимая ошибка имеет матрицу, которая, кажется, является положительно-определенной, но на самом деле имеет почти нулевое оцененное собственное значение к в точности машины. Для этого с ковариацией оценивают Covariance, используйте cond(Covariance), где любое значение, больше, чем 1/eps должен быть рассмотрен подозреваемым.

Если любой тип отказа происходит, однако, примечание, что стандартная программа регрессии указывает, что что-то, вероятно, неправильно с данными. (Даже без недостающих данных, два временных рядов, которые пропорциональны друг другу, производят сингулярную ковариационную матрицу.)