Современный подход к охарактеризованию целей эффективности с обратной связью должен измерить размер определенных матриц передаточной функции с обратной связью с помощью различных матричных норм. Матричные нормы обеспечивают меру того, как сигналы крупносерийного производства могут добраться для определенных классов входных сигналов. Оптимизация этих типов целей эффективности на множестве стабилизировавшихся контроллеров является основной тягой недавней теории оптимального управления, такой как L 1, H 2, H∞ и оптимальное управление. Следовательно, важно понять, сколько типов целей управления может быть изложено как минимизация передаточных функций с обратной связью.
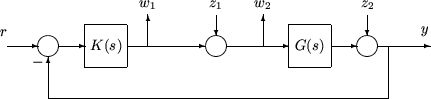
Рассмотрите задачу отслеживания, с подавлением помех, шумом измерения, и управляйте ограничениями входного сигнала, как показано в Обобщенной и Взвешенной Блок-схеме Эффективности. K является некоторым контроллером, чтобы быть спроектированным, и G является системой, которой вы хотите управлять.
Типичная цель эффективности с обратной связью
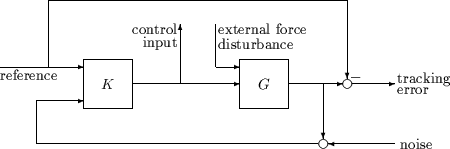
Разумное, хотя не точный, проектирует цель, был бы к проекту K, чтобы продолжить отслеживать ошибки и входной сигнал управления, маленький для всех разумных ссылочных команд, шумов датчика и внешних воздействий силы.
Следовательно, естественная цель эффективности является усилением с обратной связью от внешних влияний (ссылочные команды, шум датчика и внешние воздействия силы) к отрегулированным переменным (отслеживающий ошибки и входной сигнал управления). А именно, позвольте T обозначить отображение с обратной связью от внешних влияний до отрегулированных переменных:
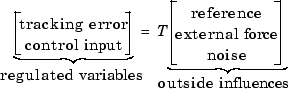
Можно оценить эффективность путем измерения усиления от внешних влияний до отрегулированных переменных. Другими словами, хорошая эффективность сопоставлена с бывшим малым T. Поскольку система с обратной связью является мультивходом, мультивыведите (MIMO) динамическую систему, существует два различных аспекта к усилению T:
Пространственный (векторные воздействия и векторные ошибки)
Временный (динамическое отношение между сигналами ввода/вывода)
Следовательно критерий производительности должен составлять
Относительная величина внешних влияний
Зависимость частоты сигналов
Относительная важность величин отрегулированных переменных
Таким образом, если цель эффективности в форме матричной нормы, это должна на самом деле быть взвешенная норма
∥WLTWR ∥
Цели эффективности с обратной связью формулируются как взвешенные передаточные функции с обратной связью, которые должны быть сделаны маленькими через обратную связь. Типовой пример, который включает много соответствующих терминов, показывают в форме блок-схемы в Обобщенной и Взвешенной Блок-схеме Эффективности. В схеме G обозначает модель объекта управления, и K является контроллером обратной связи.
Обобщенная и взвешенная блок-схема эффективности
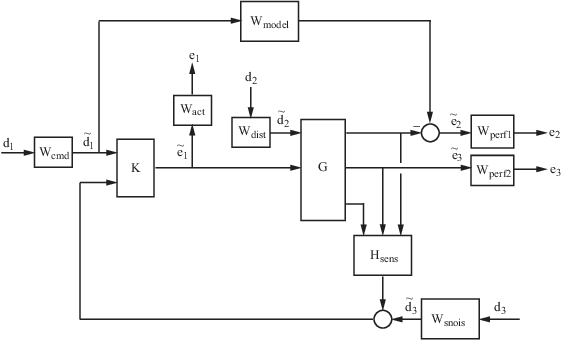
Блоки в этом рисунке могут быть скалярными (SISO) и/или многомерными (MIMO), в зависимости от определенного примера. Математическая цель H ∞ управление состоит в том, чтобы сделать передаточную функцию MIMO с обратной связью, Тед удовлетворяет ∥Ted ∥∞ <1. Функции взвешивания используются, чтобы масштабировать передаточные функции ввода/вывода, таким образом что когда ∥Ted ∥∞ <1, отношение между и подходит.
Требования к производительности в системе с обратной связью преобразовываются в H ∞ среда с помощью взвешивания или масштабирования функций. Веса выбраны с учетом относительной величины сигналов, их зависимости частоты и их относительной важности. Это получено на рисунке выше, где веса или масштабирования [Wcmd, Wdist, Wsnois] используются, чтобы преобразовать и масштабировать нормированные входные сигналы [d1, d2, d3] в физические единицы измерения, заданные как [d1, d2, d3]. Так же веса или масштабирования [Wact, Wperf1, Wperf2] преобразовывают и масштабируют физические единицы измерения в нормированные выходные сигналы [e1, e2, e3]. Интерпретация сигналов, функций взвешивания и моделей следует.
|
Сигнал |
Значение |
|---|---|
|
d1
|
Нормированная ссылочная команда Типичная ссылочная команда в физических единицах измерения |
|
d2
|
Нормированные внешние воздействия Типичные внешние воздействия в физических единицах измерения |
|
d3
|
Нормированный шум датчика Типичный шум датчика в физических единицах измерения |
|
e1
|
Взвешенные управляющие сигналы Фактические управляющие сигналы в физических единицах измерения |
|
e2
|
Взвешенные ошибки отслеживания Фактические ошибки отслеживания в физических единицах измерения |
|
e3
|
Взвешенные ошибки объекта Фактические ошибки объекта в физических единицах измерения |
Wcmd
Wcmd включен в H ∞ проблемы управления, которые требуют отслеживания ссылочной команды. Wcmd формирует нормированные ссылочные сигналы команды (величина и частота) в фактическое (или типичный) опорные сигналы, что вы ожидаете происходить. Это описывает величину и зависимость частоты ссылочных команд, сгенерированных нормированным опорным сигналом. Обычно Wcmd является плоским в низкой частоте и прокручивается прочь на высокой частоте. Например, в проблеме управления полетом, летчики-истребители генерируют входные команды ссылки палки до полосы пропускания приблизительно 2 Гц. Предположим, что палка имеет максимальное перемещение трех дюймов. Экспериментальные команды могли быть смоделированы, когда нормированные сигналы прошли через фильтр первого порядка:
Wmodel
Wmodel представляет желаемую идеальную модель для закрытого - циклично выполненная система и часто включается в формулировки задачи с отслеживанием требований. Включение идеальной модели для отслеживания часто называется моделью, совпадающей с проблемой, i.e., цель системы с обратной связью состоит в том, чтобы совпадать с заданной моделью. Для хорошего ответа отслеживания команды вы можете хотеть, чтобы система с обратной связью ответила как хорошо ослабленная система второго порядка. Идеальная модель затем была бы
для определенной желаемой собственной частоты ω и желаемый коэффициент затухания ζ. Модульные преобразования могут быть необходимыми, чтобы гарантировать точную корреляцию между идеальной моделью и системой с обратной связью. В примере летчика-истребителя предположите, что уровнем крена управляют, и 10º/second ответ желаем для каждого дюйма движения палки. Затем в этих модулях соответствующая модель:
Wdist
Wdist формирует содержимое частоты и величину внешних воздействий, влияющих на объект. Например, рассмотрите электронный микроскоп как объект. Доминирующая цель эффективности состоит в том, чтобы механически изолировать микроскоп от внешних механических воздействий, таких как наземные возбуждения, звук (давление) волны и воздушные потоки. Можно получить спектр и относительные величины этих воздействий с передаточной функцией, взвешивающей матричный Wdist.
Wperf1
Wperf1 взвешивает различие между ответом системы с обратной связью и идеальной моделью модели W. Часто вы можете хотеть точное соответствие идеальной модели в низкой частоте и потребовать менее точного соответствия на более высокой частоте, в этом случае Wperf1 является плоским в низкой частоте, прокручивается прочь в первом или втором порядке и выравнивается в маленьком, ненулевом значении на высокой частоте. Инверсия веса связана с допустимым размером отслеживания ошибок при контакте со ссылочными командами и воздействиями, описанными Wcmd и Wdist.
Wperf2
Wperf2 штрафует переменные, внутренние процессу G, такие как состояния привода, которые являются внутренними к G или другим переменным, которые не являются частью цели отслеживания.
Wact
Wact используется, чтобы сформировать штраф на использовании управляющего сигнала. Wact является частотой, варьирующейся, функция взвешивания раньше штрафовала пределы на отклонении/положении, уровне/скорости отклонения, и т.д., ответе управляющих сигналов, при контакте с отслеживанием и целями подавления помех, заданными выше. Каждый управляющий сигнал обычно штрафуется независимо.
Wsnois
Wsnois представляет модели частотного диапазона шума датчика. Каждая обратная связь измерения датчика контроллеру имеет некоторый шум, который часто выше в одном частотном диапазоне, чем другой. Вес Wsnois пытается получить эту информацию, выведенную из лабораторных экспериментов или на основе измерений производителя, в проблеме управления. Например, средние акселерометры класса имеют существенный шум в низкой частоте и высокой частоте. Поэтому соответствующий вес Wsnois был бы больше в низкой частоте и высокой частоте и имел бы меньшую величину в среднечастотной области значений. Измерение смещения или вращения часто довольно точно в низкой частоте и в устойчивом состоянии, но отвечает плохо, когда частота увеличивается. Функция взвешивания для этого датчика была бы мала в низкой частоте, постепенно увеличивалась бы в величине как первое - или система второго порядка и выравнивалась бы на высокой частоте.
Hsens
Hsens представляет модель динамики датчика или внешнего фильтра сглаживания. Передаточные функции, используемые, чтобы описать Hsens, основаны на физических характеристиках отдельных компонентов. Эти модели могут также быть смешаны в модель объекта управления G.
Эта типовая блок-схема имеет огромную гибкость, и много целей эффективности управления могут быть сформулированы в H ∞ среда с помощью этого описания блок-схемы.
Эффективность и компромиссы робастности в системе управления были обсуждены в контексте многомерного формирования цикла в Компромиссе Между Эффективностью и Робастностью. В H ∞ среда системы управления, можно включать цели робастности как дополнительное воздействие к ошибочным передаточным функциям — воздействия, которые будут сохранены маленькими. Рассмотрите следующую фигуру системы с обратной связью с обратной связью с аддитивными и мультипликативными моделями неопределенности.
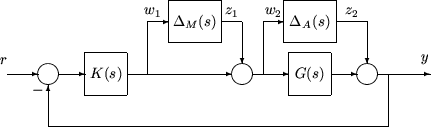
Матрицы передаточной функции заданы как:
где TI обозначает вход, дополнительная функция чувствительности и SO (s) обозначают выходную функцию чувствительности. Границы на размере матриц передаточной функции от z1 до w1 и z2 к w2 гарантируют, что система с обратной связью устойчива к мультипликативной неопределенности, ΔM (s), во входе объекта и аддитивной неопределенности, ΔA (s), вокруг объекта G (s). В H ∞ формулировка задачи управления, цели робастности вводят процедуру синтеза, когда дополнительный ввод/вывод сигнализирует, чтобы быть сохраненным маленьким. Соединение с удаленными блоками неопределенности следует.
H ∞ цель робастности управления находится теперь в том же формате как цели эффективности, то есть, чтобы минимизировать H ∞ норма матрицы передачи от z, [z1, z2], к w, [w1, w2].
Взвешивание или масштабирование матриц часто вводятся, чтобы сформировать содержимое частоты и величины чувствительности и дополнительных матриц передаточной функции чувствительности. Позвольте WM соответствовать мультипликативной неопределенности, и WA соответствуют аддитивной модели неопределенности. ΔM (s) и ΔA (s) приняты, чтобы быть нормой, ограниченной 1, т.е. | ΔM (s) | <1 и | ΔA (s) | <1. Следовательно в зависимости от частоты, |WM (jω) | и |WA (jω) | являются соответствующими размерами крупнейших ожидаемых аддитивных и мультипликативных возмущений объекта.
Мультипликативное взвешивание или масштабирование WM представляет погрешность в процентах в модели и часто мал в величине в низкой частоте, между 0,05 и 0.20 (5% к 20%, моделируя ошибку), и растя в величине на высокой частоте, 2 - 5 ((200% к 500%, моделируя ошибку). Вес перейдет путем пересечения значения величины 1, который соответствует 100%-й неопределенности в модели на частоте, по крайней мере, дважды полоса пропускания системы с обратной связью. Типичный мультипликативный вес
В отличие от этого, аддитивный вес или масштабирующий WA представляет абсолютную погрешность, которая часто мала в низкой частоте и большая в величине на высокой частоте. Величина этого веса зависит непосредственно от величины модели объекта управления, G (s).
Не выбирайте функции взвешивания с полюсами очень близко к s = 0 (z = 1 для систем дискретного времени). Например, несмотря на то, что может казаться разумным выбрать Wcmd = 1/s, чтобы осуществить нулевую установившуюся ошибку, делание так вводит нестабильный полюс, который не может быть стабилизирован, заставив синтез перестать работать. Вместо этого выберите Wcmd = 1 / (s + δ). Значение δ должно быть малым, но не очень маленькое по сравнению с системной динамикой. Например, для лучших числовых результатов, если ваша целевая частота среза составляет приблизительно 1 рад/с, выбирают δ = 0.0001 или 0.001. Точно так же в дискретное время, выберите шаги расчета, таким образом, что система и динамика взвешивания составляют не больше чем десятилетие или два ниже частоты Найквиста.
hinfstruct | hinfsyn | mixsyn